B-xor_2019牛客暑期多校训练营（第四场）

题意

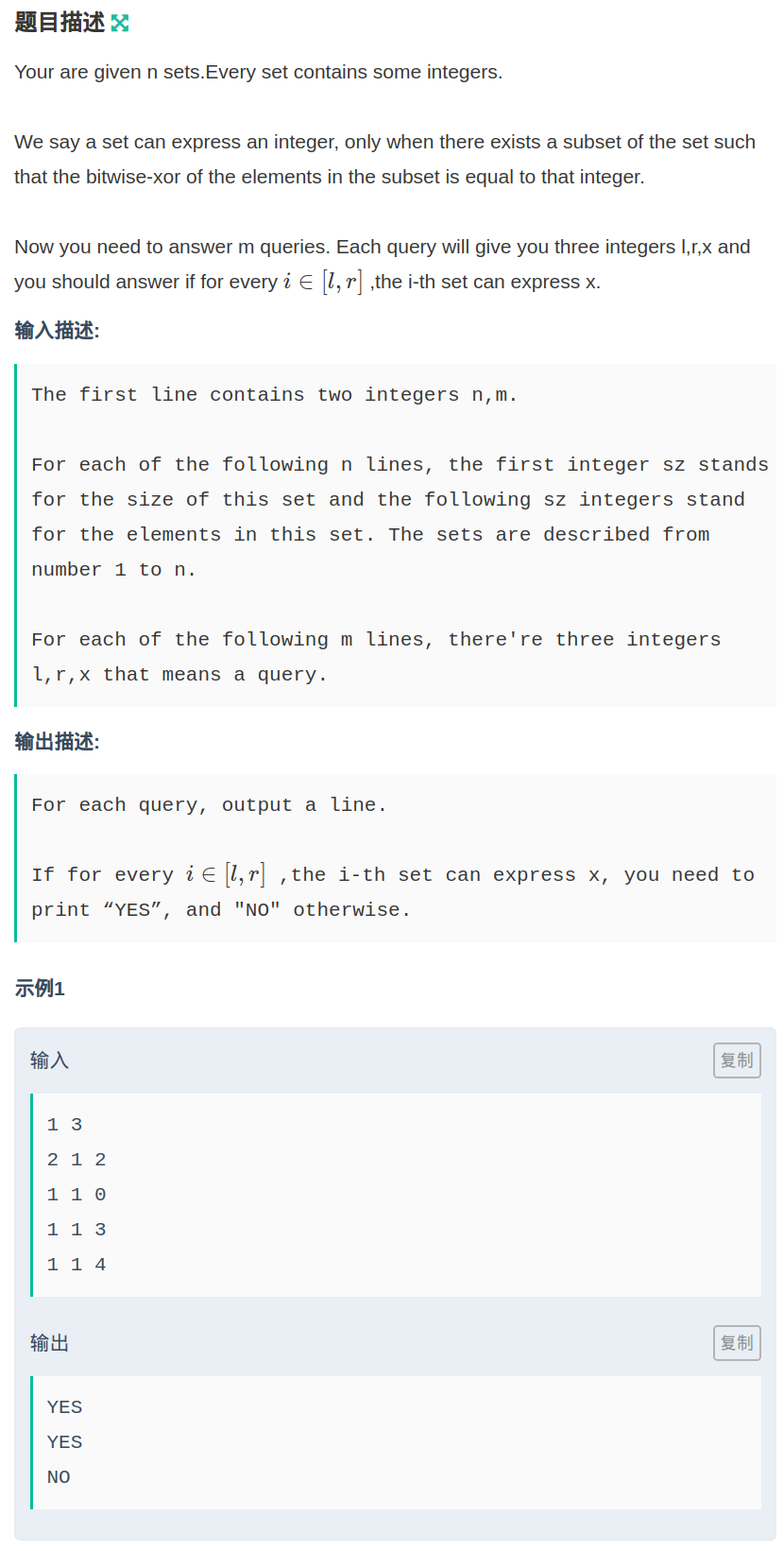
给出n个数组(每组数个数不定)，m个询问 l, r, x

序号在区间\([l,r]\)的每个数组是否都可以取出任意个数异或出x

题解

判断一个数组能否异或出x，是简单的线性基问题

判断多个线性基能否异或出x只需求出这些线性基的交，在交线性基上判断能否异或出x，多个线性基的交一定能被每个线性基分别表示，利用线段树维护区间线性基交就行，线性基求交模板是牛客上扒的咖啡鸡的

代码

#include <bits/stdc++.h>

using namespace std;
const int mx = 50000+10;
typedef unsigned int ui;

ui a[mx][35];

struct node{
    ui r[32];
    ui f[32];
    bool ins(ui x){
        for (int i=31;i>=0;i--)
            if (x>>i){
                if (!r[i]) {r[i]=x;return 1;}
                x^=r[i];
                if (!x) return 0;
            }
        return 0;
    }
    void ins2(ui x){
        ui tmp=x;
        for (int i=31;i>=0;i--)
            if (x>>i){
                if (!r[i]) {f[i]=tmp;r[i]=x;return;}
                x^=r[i]; tmp^=f[i];
                if (!x) return;
            }
        return;
    }
    bool find(ui x){
        for (int i=31;i>=0;i--)
            if (x>>i){
                if (!r[i]) return 0;
                x^=r[i];
            }
        return x==0;
    }
    ui calc(ui x){
        ui ret=0;
        for (int i=31;i>=0;i--){
            if (x>>i){
                ret^=f[i];
                x^=r[i];
            }
        }
        return ret;
    }
    void print(){
        for (int i=0;i<3;i++)cout<<r[i]<<' ';cout<<endl;
    }
    void clear(){
        for (int i=0;i<32;i++) r[i]=f[i]=0;
    }
}tree[mx<<2];

node merge(node u,node v){
    node ret,tmp;
    ret.clear(); tmp=u;
    for (int i=31;i>=0;i--) {
        ui x=v.r[i];
        if (tmp.find(x)){
            ret.ins(x^tmp.calc(x));
        } else tmp.ins2(x);
    }
    return ret;
}

void pushUp(int rt) {
    tree[rt] = merge(tree[rt<<1], tree[rt<<1|1]);
}

void build(int l, int r, int rt) {
    if (l == r) {
        for (int i = 1; i <= 32; i++)
            tree[rt].ins(a[r][i]);
        return;
    }
    int mid = (l + r) / 2;
    build(l, mid, rt<<1);
    build(mid+1, r, rt<<1|1);
    pushUp(rt);
}

bool query(int L, int R, ui x, int l, int r, int rt) {
    if (L <= l && r <= R) {
        return tree[rt].find(x);
    }
    int mid = (l + r) / 2;
    bool f1 = true, f2 = true;
    if (L <= mid) f1 = query(L, R, x, l, mid, rt<<1);
    if (mid < R) f2 = query(L, R, x, mid+1, r, rt<<1|1);
    return f1&&f2;
}

int main() {
    int n, m, sz;
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++) {
        scanf("%d", &sz);
        for (int j = 1; j <= sz; j++)
            scanf("%u", &a[i][j]);
    }
    build(1, n, 1);
    while (m--) {
        ui l, r, x;
        scanf("%u%u%u", &l, &r, &x);
        puts(query(l, r, x, 1, n, 1) ? "YES" : "NO");
    }
    return 0;
}