用Python解方程

一元一次方程

例题1：这是北师大版小学六年级上册课本95页的一道解方程练习题：

大家可以先口算一下，这道题里面的x的值为200

接下来我们用python来实现，代码如下，每一句代码后面都写有解释语：

# 一元一次方程

x = sy.symbols("x") # 申明未知数"x"

a = sy.solve((x+(1/5)*x-240),[x]) # 写入需要解的方程体

print(a)

大家应该注意到了，在写入方程体的时候，（上面的第三行代码）我们并没有原封不动的将原方程写进去，而是换了一种写法，将等号右边的数移到了等号左边（当然，移动的过程中注意要变号哦！）然后将等号丢弃，最后变成了一个式子。这个是我们的一个固定写法，大家记住就可以了。

注意：注意！！在数学里面数字和未知数相乘时中间可以不加任何符号，比如2x就代表2乘以x,但在计算机里，乘法必须写成*乘的形式。比如2*x，而不能直接写出2x，此处一定要注意！

这是运行后的结果：

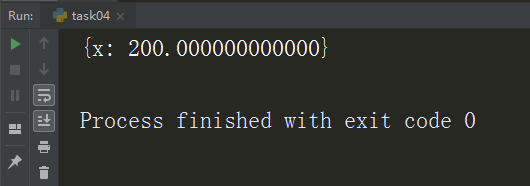
大家可以看到，结果被一对大括号包裹着，冒号前是要求的未知数，冒号后即是程序运行后得出的结果。

我们的计算机还是很聪明的，是吧！

例题2：接下来，我们再来尝试一下分式方程：

以下为2018成都市的中考数学真题A卷第8题：

用同样的程序逻辑，填好我们要求的方程，代码如下：

x = sy.symbols("x")

a = sy.solve([(x+1)/x+1/(x-2)-1],[x])

print(a)

#{x: 1}

运行结果：

二元一次方程

例题3：接下来我们来试一下两个未知数的

这是北师大版初中八年级上册课本132页的一道练习题：

用python来实现，

# 二元一次方程

x,y = sy.symbols("x y")

a = sy.solve([3*x-2*y-3,x+2*y-5],[x,y])

print(a)

# {x: 2, y: 3/2}

运行结果：

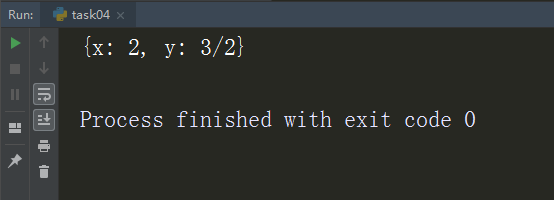
所以正确答案为：C答案

以下为2018成都市的中考数学真题B卷第21题：

用Python实现：

x,y = sy.symbols("x y")

a = sy.solve([x + y - 0.2,x + 3*y -1],[x,y])

x = a[x]

y = a[y]

re = x**2+4*x*y +4*y**2

print(re)

注意：

不要省略乘号“*”
“**”代表乘方

运行结果截图：

多元线性方程组求解

求解线性方程组比较简单，只需要用到一个函数(scipy.linalg.solve)就可以了。

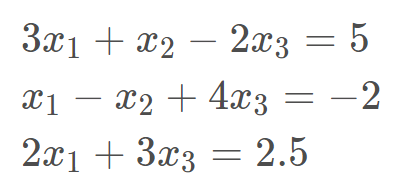
import numpy as np

from scipy.linalg import solve

#输出系数矩阵

a=np.array([[3,1,-2],[1,-1,4],[2,0,3]])

#值

b=np.array([5,-2,2.5])

#计算

x=solve(a,b)

#打印结果

print(x)

[0.5 4.5 0.5]

sympy 数学方程求解
SymPy是比较强大的，可以做到符号的化简，求值等。SymPy是符号数学的Python库。它的目标是成为一个全功能的计算机代数系统，同时保持代码简洁、易于理解和扩展。 SymPy完全是用Python写的，并不需要外部的库。

可以做到先设置变量，然后打印不需要设置值的功能，例如：在我们日常书写中print(x+y)是会报错的，然而使用了如下就不会报错了：

from sympy import *

x,y= symbols('x,y')

print(x + y+x+y)

2*x + 2*y

公式与代码之间转换：

加号 +
减号 -
除号 /
乘号 *
指数 **
对数 log()
e的指数次幂 exp()