2017四川省赛D题《Dynamic Graph》

题意：给出一个n个点m条边的有向无环图（DAG），初始的时候所有的点都为白色。然后有Q次操作，每次操作要把一个点的颜色改变，白色<->黑色，对于每次操作，输出满足下列点对<u,v>,u，v都为白色且可以相互到达的个数。

数据范围：

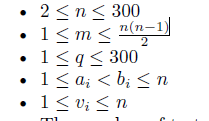
DAG上的问题，首先最暴力的方法就是，对于每一次更改都进行一遍dfs,B[u][v]，表示U点可以到达v点，然后对于U的父亲结点来说，暴力合并，复杂度约为n^4,这样显然会爆炸。解法是每次用BITSET优化，因为B[u][v]的状态非零即一。

代码如下：

#include<bits/stdc++.h>
typedef long long LL;
using namespace std;
const int maxn = 350;
int N, M, Q;
struct Edge
{
    int to, next;
    Edge(int to = 0, int next = 0): to(to), next(next) {}
} E[maxn * maxn];
int head[maxn], tot;
void initedge()
{
    memset(head, -1, sizeof(head));
    tot = 0;
}
void addedge(int u, int v)
{
    E[tot] = Edge(v, head[u]);
    head[u] = tot++;
}
bitset<maxn>BT[maxn];
int vis[maxn], cul[maxn];
void init()
{
    for(int i = 0; i <= N; i++)
    {
        BT[i].reset();
        vis[i] = cul[i] = 0;
    }
}
void DFS(int u)
{
    BT[u].reset();
    BT[u][u] = 1;
    vis[u] = 1;
    if(cul[u]) return ;
    for(int k = head[u]; ~k; k = E[k].next)
    {
        int v = E[k].to;
        if(!vis[v]) DFS(v);
        if(!cul[v]) BT[u] |= BT[v];
    }
}
int main ()
{
    while(~scanf("%d %d %d", &N, &M, &Q))
    {
        init();
        initedge();
        for(int i = 1; i <= M; i++)
        {
            int u, v;
            scanf("%d %d", &u, &v);
            addedge(u, v);
        }
        for(int i = 1; i <= Q; i++)
        {
            int u, ans = 0;
            scanf("%d", &u);
            cul[u] ^= 1;
            for(int i = 1; i <= N; i++) vis[i] = 0;
            for(int i = 1; i <= N; i++)
            {
                if(!vis[i]) DFS(i);
                ans += BT[i].count() - 1;
            }
            printf("%d\n", ans);
        }
    }
    return 0;
}

另外还有一种方法：

维护F[u][v],表示u->v的路径条数，然后对于每次操作更新F[u][v]-+=F[u][x]*F[x][v]，然后判断F[u][v]是否>0即可,这样做是对的，但是F[u][v]可能非常大，要用unsigned long long ,虽然unsigned long long 存不下，但是他有自动取模的功能，即使是这样也有可能出现F[u][v]之间有路径，但是取模后为0的情况，但是这个概率是很小的，unsigned long long 已经很大了，取模后出现零的情况应该不会被卡。unsigned int 也可以过。

代码如下：

#include<bits/stdc++.h>
using namespace std;
typedef unsigned long long LL;
const int maxn = 350;
LL dp[maxn][maxn], vis[maxn];
int N, M, Q;
void init()
{
    for(int i = 1; i <= N; i++)
    {
        vis[i] = 0;
        for(int j = 1; j <= N; j++)
            dp[i][j] = 0;
    }
}
int main ()
{
    while(~scanf("%d %d %d", &N, &M, &Q))
    {
        init();
        for(int i = 1; i <= M; i++)
        {
            int u, v;
            scanf("%d %d", &u, &v);
            dp[u][v]++;
        }
        for(int k = 1; k <= N; k++ )
            for(int st = 1; st < k; st++)
                for(int ed = k + 1; ed <= N; ed++)
                    dp[st][ed] += dp[st][k] * dp[k][ed];
        for(int i = 1; i <= Q; i++)
        {
            int u;
            scanf("%d", &u);
            if(vis[u] == 0)
            {
                vis[u] = 1;
                for(int st = 1; st < u; st++)
                    for(int ed = u + 1; ed <= N; ed++)
                        dp[st][ed] -= dp[st][u] * dp[u][ed];
            }
            else
            {
                vis[u] = 0;
                for(int st = 1; st < u; st++)
                    for(int ed = u + 1; ed <= N; ed++)
                        dp[st][ed] += dp[st][u] * dp[u][ed];
            }
            int ans = 0;
            for(int st = 1; st <= N; st++)
            {
                if(vis[st]) continue;
                for(int ed = st + 1; ed <= N; ed++)
                {
                    if(vis[ed]) continue;
                    if(dp[st][ed] > 0) ans++;
                }
            }
            printf("%d\n", ans);
        }
    }
    return 0;
}