回溯算法_01背包问题_Java实现

原文地址：http://blog.csdn.net/ljmingcom304/article/details/50314839

本文出自：【梁敬明的博客】

1.回溯算法　　

　　回溯算法也叫试探法，通俗的将就是一个方向的路一直往前走，能走则走，不能走则退回来换一个方向再试。一般的实现步骤是：针对一个问题定义解的空间，至少包含问题的一个最优解；用易于搜索的解空间结构，使得能用回溯方法搜索整个解空间；以深度优先的方式搜索整个解空间，并在搜索过程中通过剪枝函数避免无效搜索。

回溯算法

　　

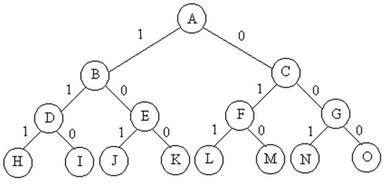
　　如上图所示，每个节点均有左右两种选择，最终要实现结果会产生AH、AI、AJ、AK、AL、AM、AN和AO八种实现方案，需要确定哪种方案为最优方案。以左边的条件为首要条件进行判断，那么其搜索路线为：【A】→【B】→【D】→【H】→【I】→【E】→【J】→【Ｋ】→【C】→【F】→【L】→【M】→【G】→【N】→【O】，即在全部满足限制条件的前提下，实现每个节点之间的两两比较，最终选择出最优方案。

2.背包问题　　

　　一个旅行者有一个最多能装m公斤的背包，现在有n中物品，每件的重量分别是W1、W2、……、Wn，每件物品的价值分别为C1、C2、……、Cn， 需要将物品放入背包中，要怎么样放才能保证背包中物品的总价值最大？

3.算法分析　

　　上述问题包含两种情况，一种是将物品放入背包中，另一种是不将物品放入背包中。其中隐含着三个限制条件。第一个限制条件为放入物品的总和不能超过背包的总承重，即当放入的物品总和超过背包的总承重时，即使背包中物品的总价值再大也毫无意义。第二个限制条件为要保证背包中物品的总价值最大。无论第一个条件成不成立，第二个条件总是在其之上的一种更优的选择。第三个限制条件为当达到物品的数量上限，即没有可以获取物品再放入背包时，前两个限制条件均毫无意义，因此需要优先进行判断。

　　这里我们可以将第一种情况看做左节点，第二种情况看做右节点，第三个限制条件用于终结节点的搜索。因此在解决该问题时，首先需要判断是否有物品可以放到背包中，要是没有物品可以放到背包中，直接返回结果，当前的价值即为背包的最优价值。然后判断左节点是否为可行节点，当左节点可行，就优先搜索左子树，不满足则进入右子树。当达到物品的数量上限，直接返回当前物品数量的结果；若左右节点同时不可行，则直接将结果返回上一步。以此类推，将结果从下至上一层一层进行返回，得到问题的最优结果。

　　创建一个物品对象，分别存在价值、重量以及单位重量价值三种属性。

public class Knapsack implements Comparable<Knapsack> {
    /** 物品重量 */
    private int weight;
    /** 物品价值 */
    private int value;
    /** 单位重量价值 */
    private int unitValue;

    public Knapsack(int weight, int value) {
        this.weight = weight;
        this.value = value;
        this.unitValue = (weight == 0) ? 0 : value / weight;
    }

    public int getWeight() {
        return weight;
    }

    public void setWeight(int weight) {
        this.weight = weight;
    }

    public int getValue() {
        return value;
    }

    public void setValue(int value) {
        this.value = value;
    }

    public int getUnitValue() {
        return unitValue;
    }

    @Override
    public int compareTo(Knapsack snapsack) {
        int value = snapsack.unitValue;
        if (unitValue > value)
            return 1;
        if (unitValue < value)
            return -1;
        return 0;
    }

}

按照回溯算法将物品放入背包中。

public class HSSFProblem {

    // 待选择的物品
    private Knapsack[] bags;
    // 背包的总承重
    private int totalWeight;
    // 背包的当前承重
    private int currWeight;
    // 待选择物品数量
    private int n;
    // 放入物品后背包的最优价值
    private int bestValue;
    // 放入物品和背包的当前价值
    private int currValue;

    public HSSFProblem(Knapsack[] bags, int totalWeight) {
        this.bags = bags;
        this.totalWeight = totalWeight;
        this.n = bags.length;

        // 物品依据单位重量价值从大到小进行排序
        Arrays.sort(bags, Collections.reverseOrder());
    }

    public int solve(int i) {

        // 当没有物品可以放入背包时，当前价值为最优价值
        if (i >= n) {
            bestValue = currValue;
            return bestValue;
        }

        // 首要条件：放入当前物品，判断物品放入背包后是否小于背包的总承重
        if (currWeight + bags[i].getWeight() <= totalWeight) {
            // 将物品放入背包中的状态
            currWeight += bags[i].getWeight();
            currValue += bags[i].getValue();

            // 选择下一个物品进行判断
            bestValue = solve(i + 1);

            // 将物品从背包中取出的状态
            currWeight -= bags[i].getWeight();
            currValue -= bags[i].getValue();
        }

        // 次要条件：不放入当前物品，放入下一个物品可能会产生更优的价值，则对下一个物品进行判断
        // 当前价值+剩余价值<=最优价值，不需考虑右子树情况，由于最优价值的结果是由小往上逐层返回，
        // 为了防止错误的将单位重量价值大的物品错误的剔除，需要将物品按照单位重量价值从大到小进行排序
        if (currValue + getSurplusValue(i + 1) > bestValue) {
            // 选择下一个物品进行判断
            bestValue = solve(i + 1);
        }
        return bestValue;
    }

    // 获得物品的剩余总价值
    public int getSurplusValue(int i) {
        int surplusValue = 0;
        for (int j = i; j < n; j++)
            surplusValue += bags[i].getValue();
        return surplusValue;
    }

}

最终测试结果：90

public class HSSFTest {
public static void main(String[] args) {
    Knapsack[] bags = new Knapsack[] { new Knapsack(2, 13),
            new Knapsack(1, 10), new Knapsack(3, 24), new Knapsack(2, 15),
            new Knapsack(4, 28), new Knapsack(5, 33), new Knapsack(3, 20),
            new Knapsack(1, 8) };
    int totalWeight = 12;
    HSSFProblem problem = new HSSFProblem(bags, totalWeight);

    System.out.println(problem.solve(0));
}
}

欢迎关注我的微信公众号：“”Java面试通关手册（坚持原创，分享美文，分享各种Java学习资源，面试题，以及企业级Java实战项目回复关键字免费领取）：