《attention is all you need》解读

Motivation:

靠attention机制，不使用rnn和cnn，并行度高
通过attention，抓长距离依赖关系比rnn强

创新点：

通过self-attention，自己和自己做attention，使得每个词都有全局的语义信息（长依赖
由于 Self-Attention 是每个词和所有词都要计算 Attention，所以不管他们中间有多长距离，最大的路径长度也都只是 1。可以捕获长距离依赖关系
提出multi-head attention，可以看成attention的ensemble版本，不同head学习不同的子空间语义。

attention表示成k、q、v的方式:

传统的attention(sequence2sequence问题)：

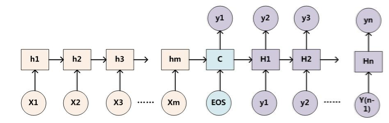
上下文context表示成如下的方式（h的加权平均）：

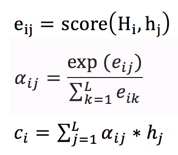
那么权重alpha（attention weight）可表示成Q和K的乘积，小h即V（下图中很清楚的看出，Q是大H，K和V是小h）：

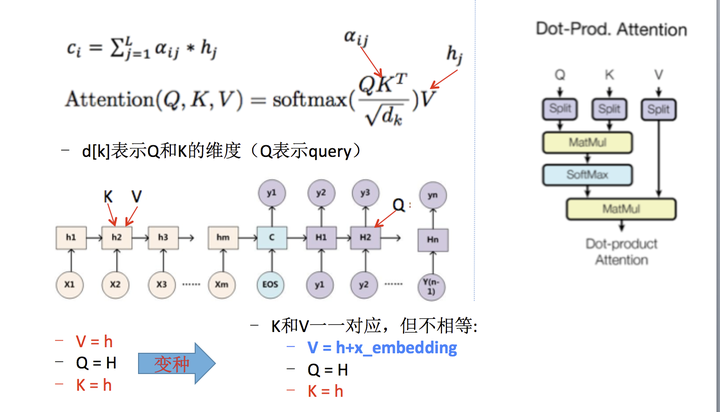
上述可以做个变种，就是K和V不相等，但需要一一对应，例如：

V=h+x_embedding
Q = H
k=h

乘法VS加法attention

加法注意力：

还是以传统的RNN的seq2seq问题为例子，加性注意力是最经典的注意力机制，它使用了有一个隐藏层的前馈网络（全连接）来计算注意力分配：

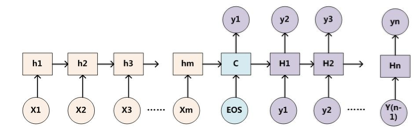
乘法注意力：

就是常见的用乘法来计算attention score：

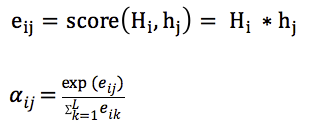
乘法注意力不用使用一个全连接层，所以空间复杂度占优；另外由于乘法可以使用优化的矩阵乘法运算，所以计算上也一般占优。

论文中的乘法注意力除了一个scale factor:

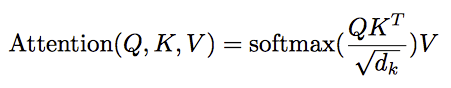
论文中指出当dk比较小的时候，乘法注意力和加法注意力效果差不多；但当d_k比较大的时候，如果不使用scale factor，则加法注意力要好一些，因为乘法结果会比较大，容易进入softmax函数的“饱和区”，梯度较小。

self-attention

以一般的RNN的S2S为例子，一般的attention的Q来自Decoder（如下图中的大H），K和V来自Encoder（如下图中的小h）。self-attention就是attention的K、Q、V都来自encoder或者decoder，使得每个位置的表示都具有全局的语义信息，有利于建立长依赖关系。

Layer normalization(LN)

batch normalization是对一个每一个节点，针对一个batch，做一次normalization，即纵向的normalization:

layer normalization(LN)，是对一个样本，同一个层网络的所有神经元做normalization，不涉及到batch的概念，即横向normalization:

BN适用于不同mini batch数据分布差异不大的情况，而且BN需要开辟变量存每个节点的均值和方差，空间消耗略大；而且 BN适用于有mini_batch的场景。

LN只需要一个样本就可以做normalization，可以避免 BN 中受 mini-batch 数据分布影响的问题，也不需要开辟空间存每个节点的均值和方差。

但是，BN 的转换是针对单个神经元可训练的——不同神经元的输入经过再平移和再缩放后分布在不同的区间，而 LN 对于一整层的神经元训练得到同一个转换——所有的输入都在同一个区间范围内。如果不同输入特征不属于相似的类别（比如颜色和大小，scale不一样），那么 LN 的处理可能会降低模型的表达能力。

encoder:

输入：和conv s2s类似，词向量加上了positional embedding，即给位置1，2，3，4...n等编码（也用一个embedding表示）。然后在编码的时候可以使用正弦和余弦函数，使得位置编码具有周期性，并且有很好的表示相对位置的关系的特性（对于任意的偏移量k，PE[pos+k]可以由PE[pos]表示）：

输入的序列长度是n，embedding维度是d，所以输入是n*d的矩阵
N=6，6个重复一样的结构，由两个子层组成：

子层1:

Multi-head self-attention
残余连接和LN：

Output = LN (x+sublayer(x))

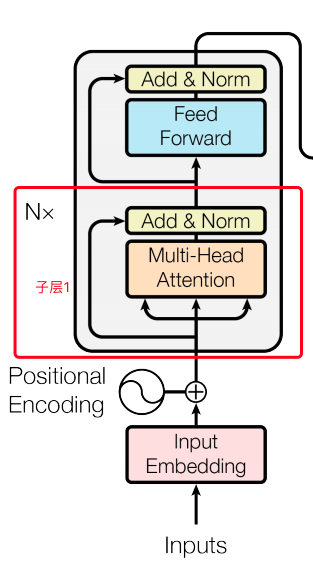
子层2:

Position-wise fc层(跟卷积很像)
对n*d的矩阵的每一行进行操作（相当于把矩阵每一行铺平，接一个FC），同一层的不同行FC层用一样的参数，不同层用不同的参数(对于全连接的节点数目，先从512变大为2048，再缩小为512)，这里的max表示使用relu激活函数：

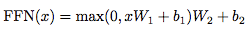
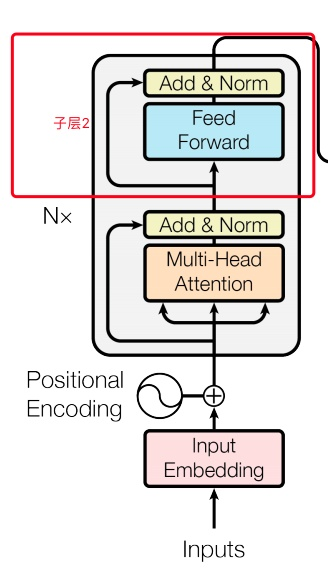
整个encoder的输出也是n*d的矩阵

decoder:

•输入:假设已经翻译出k个词，向量维度还是d

•同样使用N=6个重复的层，依然使用残余连接和LN

•3个子层，比encoder多一个attention层，是Decoder端去attend encoder端的信息的层:

Sub-L1:
self-attention，同encoder，但要Mask掉未来的信息，得到k*d的矩阵

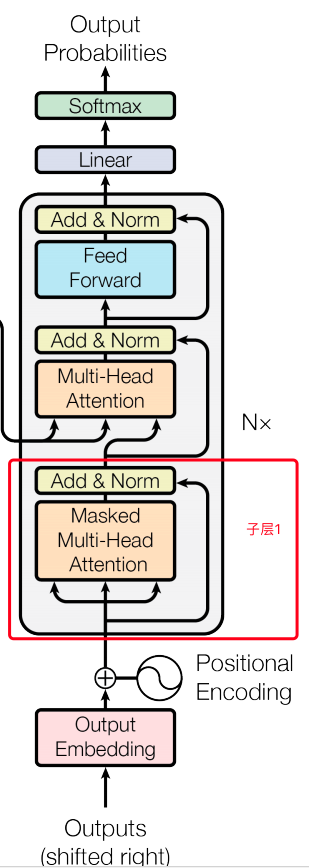
Sub-L2:和encoder做attention的层，输出k*d的矩阵
Sub-L3:全连接层，输出k*d的矩阵，用第k行去预测输出y

mutli-head attention:

MultiHead可以看成是一种ensemble方式，获取不同子空间的语义:

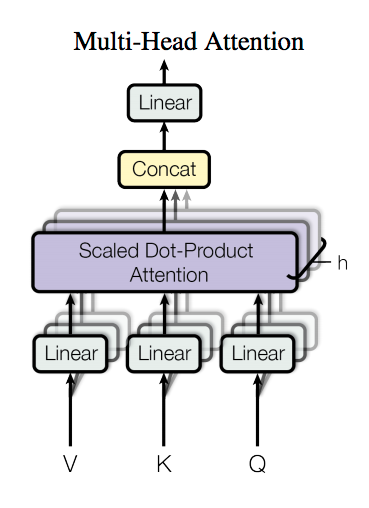
获取每个子任务的Q、K、V：

通过全连接进行线性变换映射成多个Q、K、V，线性映射得到的结果维度可以不变、也可以减少(类似降维)
或者通过Split对Q、K、V进行划分(分段)

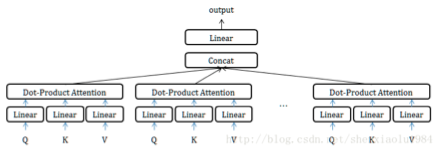
如果采用线性映射的方式，使得维度降低；或者通过split的方式使得维度降低，那么多个head做attention合并起来的复杂度和原来一个head做attention的复杂度不会差多少，而且多个head之间做attention可以并行。

总结

本文提出用attention做翻译，不用RNN和CNN，attention计算快，并行度高，而且任何两个词的距离都是1，抓长距离依赖擅长。但是如果要堆那么多层的话，其实也不见得快到哪里去。

另外，说一些我的经验，不一定放诸四海皆准，仅供参考（我是在语义匹配里的任务的经验，不是翻译）：

positional encoding一般可以加快收敛，但是对提升效果一般作用微小
multi-head attention在emb较小时，例如128，一般无效果。但是像原文中的512就可能有用。但是对工业界的系统，emb开不到512，内存没那么大。
attention和gru一起用，效果会有提升，在匹配任务里，attention替换不了gru，但是attention计算快。

参考文献：

https://arxiv.org/abs/1706.03762

https://arxiv.org/pdf/1711.02132.pdf

详解深度学习中的 Normalization，不只是BN（2）

BERT大火却不懂Transformer？读这一篇就够了