洛谷 P2486 [SDOI2011]染色 树链剖分

目录

• 题面
  • 题目链接
  • 题目描述
  • 输入输出格式
    • 输入格式
    • 输出格式
  • 输入输出样例
    • 输入样例：
    • 输出样例：
  • 说明
• 思路
  • PushDown与Update
  • Q
• AC代码
• 总结与拓展

题面

题目链接

P2486 [SDOI2011]染色

题目描述

输入输出格式

输入格式

输出格式

对于每个询问操作，输出一行答案。

输入输出样例

输入样例：

6 5
2 2 1 2 1 1
1 2
1 3
2 4
2 5
2 6
Q 3 5
C 2 1 1
Q 3 5
C 5 1 2
Q 3 5

输出样例：

3
1
2

说明

【数据规模】

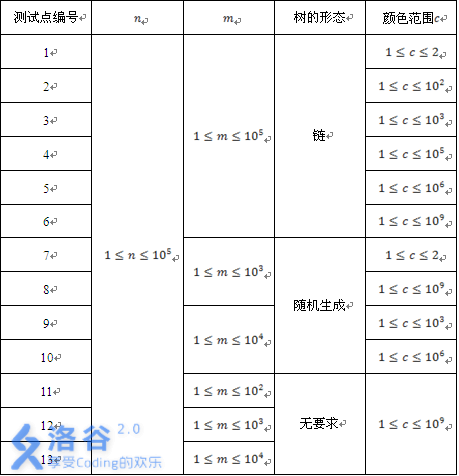
【时空限制】

1000ms,128M

思路

看题，操作从a到b的路径上所有点，可以想到树剖。

然而这一题要求的结果有点迷，如果是线段树，第一感觉是要用线段树合并。结构体里面保存 最左端的颜色nowl 和 最右端的颜色nowr ，在两个线段树合并时， 该区间内颜色段数量sum 需要作一下判断：如果左儿子的最右端和右儿子的最左端颜色相同，那么sum应该是左儿子和右儿子的sum之和减1；否则是左儿子和右儿子的sum之和。

基本思路确定了，再看看实际。。。

PushDown与Update

void Update(int p)
{
    s(p)=s(p<<1)+s(p<<1|1);
    if(nr(p<<1)==nl(p<<1|1)) s(p)--; ///如上所说的判断
    nl(p)=nl(p<<1);
    nr(p)=nr(p<<1|1);
}

void PushDown(int p)
{
    if(t(p))
    {
        s(p<<1)=s(p<<1|1)=1; ///此时两个儿子的sum都是1
        nl(p<<1)=nr(p<<1)=nl(p<<1|1)=nr(p<<1|1)=t(p<<1)=t(p<<1|1)=t(p);  ///左、右儿子最左、最右结点，还有懒标记全部变成了现在染上的颜色
        t(p)=0;
    }
}

Q

本来以为查询操作也是线段树合并，然后写了一半发现不对劲，因为查询的路径上新给定的标号nid是不连续的！不过，nid不连续，我们可以直接判断。

int Ask2(int u,int v)
{
    int ans=0;
    while(top[u]!=top[v])
    {
        if(dep[top[u]]<dep[top[v]]) swap(u,v);
        SegmentTree tmp=Ask1(1,nid[top[u]],nid[u]);
        ans+=tmp.sum; ///统计答案的时候把单独的这条链的颜色段数量加上
        if(tmp.nl==Ask1(1,nid[fa[top[u]]],nid[fa[top[u]]]).nr) ans--; ///考虑到，如果这条链可以和下一条链合并，那必然是他和他的父亲合并，所以这个时候只要判断他和他父亲颜色是否相同，来判断是否要减1
        u=fa[top[u]];
    }
    if(dep[u]>dep[v]) swap(u,v);
    ans+=Ask1(1,nid[u],nid[v]).sum;
    return ans;
}

AC代码

#include<bits/stdc++.h>
const int maxn=100010;
using namespace std;

int n,m,wt[maxn];
int tot,to[maxn<<1],nxt[maxn<<1],head[maxn];
int son[maxn],fa[maxn],len[maxn],dep[maxn];
int cnt,nid[maxn],nw[maxn],top[maxn];
struct SegmentTree
{
    int l,r,sum,nl,nr,tag;
    #define l(a) tree[a].l
    #define r(a) tree[a].r
    #define m(a) ((l(a)+r(a))>>1)
    #define len(a) (r(a)-l(a)+1)
    #define s(a) tree[a].sum
    #define nl(a) tree[a].nl
    #define nr(a) tree[a].nr
    #define t(a) tree[a].tag
}tree[maxn<<2];

void dfs1(int u,int f,int d)
{
    fa[u]=f;dep[u]=d;len[u]=1;
    for(int i=head[u];i;i=nxt[i])
    {
        int v=to[i];
        if(v==f) continue;
        dfs1(v,u,d+1);
        len[u]+=len[v];
        if(len[v]>len[son[u]]) son[u]=v;
    }
}

void dfs2(int p,int t)
{
    nid[p]=++cnt;
    nw[cnt]=wt[p];
    top[p]=t;
    if(!son[p]) return;
    dfs2(son[p],t);
    for(int i=head[p];i;i=nxt[i])
    {
        int v=to[i];
        if(v==fa[p] || v==son[p]) continue;
        dfs2(v,v);
    }
}

void Update(int p)
{
    s(p)=s(p<<1)+s(p<<1|1);
    if(nr(p<<1)==nl(p<<1|1)) s(p)--;
    nl(p)=nl(p<<1);
    nr(p)=nr(p<<1|1);
}

void BuildTree(int p,int l,int r)
{
    l(p)=l;r(p)=r;
    if(l==r)
    {
        s(p)=1;
        nl(p)=nr(p)=nw[l];
        return;
    }
    BuildTree(p<<1,l,m(p));
    BuildTree(p<<1|1,m(p)+1,r);
    Update(p);
}

void PushDown(int p)
{
    if(t(p))
    {
        s(p<<1)=s(p<<1|1)=1;
        nl(p<<1)=nr(p<<1)=nl(p<<1|1)=nr(p<<1|1)=t(p<<1)=t(p<<1|1)=t(p);
        t(p)=0;
    }
}

void Change1(int p,int l,int r,int k)
{
    if(l<=l(p) && r>=r(p))
    {
        s(p)=1;
        nl(p)=nr(p)=t(p)=k;
        return;
    }
    PushDown(p);
    if(l<=m(p)) Change1(p<<1,l,r,k);
    if(r>m(p)) Change1(p<<1|1,l,r,k);
    Update(p);
}

void Change2(int u,int v,int k)
{
    while(top[u]!=top[v])
    {
        if(dep[top[u]]<dep[top[v]]) swap(u,v);
        Change1(1,nid[top[u]],nid[u],k);
        u=fa[top[u]];
    }
    if(dep[u]>dep[v]) swap(u,v);
    Change1(1,nid[u],nid[v],k);
}

SegmentTree Ask1(int p,int l,int r)
{
    if(l<=l(p) && r>=r(p)) return tree[p];
    PushDown(p);
    if(r<=m(p)) return Ask1(p<<1,l,r);
    else if(l>m(p)) return Ask1(p<<1|1,l,r);
    else
    {
        SegmentTree a=Ask1(p<<1,l,r),b=Ask1(p<<1|1,l,r),tmp;
        tmp.nl=a.nl;tmp.nr=b.nr;
        tmp.sum=a.sum+b.sum;
        if(a.nr==b.nl) tmp.sum--;
        return tmp;
    }
}

int Ask2(int u,int v)
{
    int ans=0;
    while(top[u]!=top[v])
    {
        if(dep[top[u]]<dep[top[v]]) swap(u,v);
        SegmentTree tmp=Ask1(1,nid[top[u]],nid[u]);
        ans+=tmp.sum;
        if(tmp.nl==Ask1(1,nid[fa[top[u]]],nid[fa[top[u]]]).nr) ans--;
        u=fa[top[u]];
    }
    if(dep[u]>dep[v]) swap(u,v);
    ans+=Ask1(1,nid[u],nid[v]).sum;
    return ans;
}

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) scanf("%d",&wt[i]);
    for(int i=1;i<n;i++)
    {
        int u,v;scanf("%d%d",&u,&v);
        to[++tot]=v;nxt[tot]=head[u];head[u]=tot;
        to[++tot]=u;nxt[tot]=head[v];head[v]=tot;
    }
    dfs1(1,1,1);
    dfs2(1,1);
    BuildTree(1,1,n);
    for(int i=1;i<=m;i++)
    {
        char ch;cin>>ch;
        int u,v,k;scanf("%d%d",&u,&v);
        if(ch=='C')
        {
            scanf("%d",&k);
            Change2(u,v,k);
        }
        else printf("%d\n",Ask2(u,v));
    }
    return 0;
}

总结与拓展

感觉有点没讲清楚。这道题写完应该是对树剖有了进一步的巩固。