从头学pytorch(六):权重衰减
深度学习中常常会存在过拟合现象,比如当训练数据过少时,训练得到的模型很可能在训练集上表现非常好,但是在测试集上表现不好.
应对过拟合,可以通过数据增强,增大训练集数量.我们这里先不介绍数据增强,先从模型训练的角度介绍常用的应对过拟合的方法.
权重衰减
权重衰减等价于 \(L_2\) 范数正则化(regularization)。正则化通过为模型损失函数添加惩罚项使学出的模型参数值较小,是应对过拟合的常用手段。我们先描述\(L_2\)范数正则化,再解释它为何又称权重衰减。
\(L_2\)范数正则化在模型原损失函数基础上添加\(L_2\)范数惩罚项,从而得到训练所需要最小化的函数。\(L_2\)范数惩罚项指的是模型权重参数每个元素的平方和与一个正的常数的乘积。线性回归一文中的线性回归损失函数
\]
为例,其中\(w_1, w_2\)是权重参数,\(b\)是偏差参数,样本\(i\)的输入为\(x_1^{(i)}, x_2^{(i)}\),标签为\(y^{(i)}\),样本数为\(n\)。将权重参数用向量\(\boldsymbol{w} = [w_1, w_2]\)表示,带有\(L_2\)范数惩罚项的新损失函数为
\]
其中超参数\(\lambda > 0\)。当权重参数均为0时,惩罚项最小。当\(\lambda\)较大时,惩罚项在损失函数中的比重较大,这通常会使学到的权重参数的元素较接近0。当\(\lambda\)设为0时,惩罚项完全不起作用。上式中\(L_2\)范数平方\(\|\boldsymbol{w}\|^2\)展开后得到\(w_1^2 + w_2^2\)。
显然,相比没有正则化项的loss,有了\(L_2\)范数惩罚项后求导后将多出来一项\({\lambda}w_i\),所以,在小批量随机梯度下降中,权重\(w_1\)和\(w_2\)的迭代方式将变为
w_1 &\leftarrow \left(1- \frac{\eta\lambda}{|\mathcal{B}|} \right)w_1 - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}}x_1^{(i)} \left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b - y^{(i)}\right),\\
w_2 &\leftarrow \left(1- \frac{\eta\lambda}{|\mathcal{B}|} \right)w_2 - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}}x_2^{(i)} \left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b - y^{(i)}\right).
\end{aligned}
\]
可见,\(L_2\)范数正则化令权重\(w_1\)和\(w_2\)先自乘小于1的数,再减去不含惩罚项的梯度。因此,\(L_2\)范数正则化又叫权重衰减.
权重衰减通过惩罚绝对值较大的模型参数为需要学习的模型增加了限制,这可能对过拟合有效。实际场景中,我们有时也在惩罚项中添加偏差元素的平方和。
高维线性回归实验
我们创建一个数据集,来模拟过拟合,以及权重衰减针对过拟合的效果.
设数据样本特征的维度为\(p\)。对于训练数据集和测试数据集中特征为\(x_1, x_2, \ldots, x_p\)的任一样本,我们使用如下的线性函数来生成该样本的标签:
\]
其中噪声项\(\epsilon\)服从均值为0、标准差为0.01的正态分布。为了较容易地观察过拟合,我们考虑高维线性回归问题,如设维度\(p=200\);同时,我们特意把训练数据集的样本数设低,如20。
导入必要的包
import torch
import torch.nn as nn
import numpy as np
数据集创建
n_train, n_test, num_inputs = 20, 100, 200
true_w, true_b = torch.ones(num_inputs, 1) * 0.01, 0.05
features = torch.randn((n_train + n_test, num_inputs))
labels = torch.matmul(features, true_w) + true_b
labels += torch.tensor(np.random.normal(0, 0.01,
size=labels.size()), dtype=torch.float)
train_features, test_features = features[:n_train, :], features[n_train:, :]
train_labels, test_labels = labels[:n_train], labels[n_train:]
dataset = torch.utils.data.TensorDataset(train_features, train_labels)
参数初始化
def init_params():
w = torch.rand((num_inputs, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
return [w, b]
模型定义
def linreg(X, w, b):
# print(X.dtype,b.dtype)
return torch.mm(X, w) + b
损失函数定义
由于我们想验证L2正则项的作用,所以需要定义l2_penalty(w),loss由2部分构成,一部分就是正常的均方误差,一部分是
L2正则项,用以控制w的大小. \(\lambda\)则表示这两部分误差的比例.
(y_hat - y.view(y_hat.size())) ** 2 / 2是一个shape为[batch,1]的Tensor,(w**2).sum()/2是一个标量,
他们二者相加时,后者会自动扩展成与前者相同shape的张量.
def squared_loss(y_hat, y):
# 注意这里返回的是向量, 另外, pytorch里的MSELoss并没有除以 2
return (y_hat - y.view(y_hat.size())) ** 2 / 2
def l2_penalty(w):
return (w**2).sum()/2
def total_loss(y_hat, y,w,lambd):
return (y_hat - y.view(y_hat.size())) ** 2 / 2 + lambd * (w**2).sum()/2 #这里用了广播机制
定义优化器
def sgd(params, lr, batch_size):
for param in params:
param.data -= lr * param.grad / batch_size # 注意这里更改param时用的param.data
训练
注意,在训练阶段,在反向传播时,我们计算loss时用的是total_loss,即加入了L2正则项的.在推导阶段,计算在训练集/测试集上的loss
用的是squared_loss.
batch_size, num_epochs, lr = 2, 100, 0.003
train_iter = torch.utils.data.DataLoader(dataset,batch_size=batch_size,shuffle=True)
net = linreg
def train(lamda):
w,b = init_params()
train_ls, test_ls = [], []
for epoch in range(num_epochs):
for X,y in train_iter:
y_hat = net(X,w,b)
l = total_loss(y_hat,y,w,lamda).sum()
#print(w.grad.data)
if w.grad is not None:
#print(w.grad.data)
w.grad.data.zero_()
b.grad.data.zero_()
else:
print("grad 0 epoch %d" % (epoch))
l.backward()
sgd([w,b], lr, batch_size)
#print(l.item())
train_l = squared_loss(net(train_features,w,b),train_labels)
print('epoch %d, loss %f' % (epoch + 1, train_l.mean().item()))
train_ls.append(train_l.mean().item())
test_l = squared_loss(net(test_features,w,b),test_labels)
print('epoch %d, loss %f' % (epoch + 1, test_l.mean().item()))
test_ls.append(test_l.mean().item())
d2l.semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'loss',
range(1, num_epochs + 1), test_ls, ['train', 'test'])
当train(0)时,即相当于不带正则项的loss.绘制出的曲线如下:
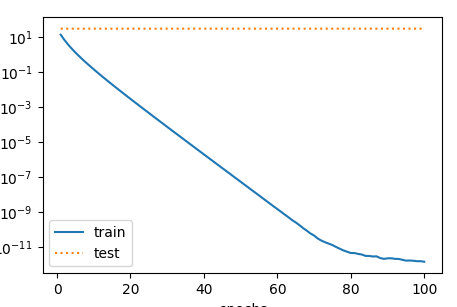
当train(1)时,即相当于squared_loss和L2正则项为1:1,绘制出的曲线如下:
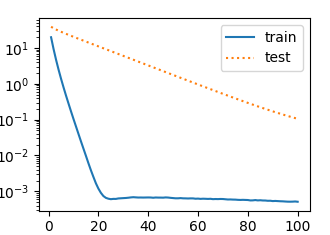
以上是我们手动实现了损失函数,优化器等.用torch里封装好的MSELoss,optim等实现如下:
def train_use_torch(wd):
net = torch.nn.Linear(num_inputs,1)
loss = nn.MSELoss()
nn.init.normal_(net.weight,mean=0,std=1)
nn.init.normal_(net.bias,mean=0,std=1)
optimizer_w =torch.optim.SGD(params=[net.weight],lr=lr,weight_decay=wd) #权重衰减
optimizer_b =torch.optim.SGD(params=[net.bias],lr=lr) #偏差参数衰减
train_ls, test_ls = [], []
for epoch in range(num_epochs):
for X,y in train_iter:
y_hat = net(X)
l = loss(y_hat,y).sum()
optimizer_w.zero_grad()
optimizer_b.zero_grad()
l.backward()
optimizer_w.step()
optimizer_b.step()
train_l = squared_loss(net(train_features),train_labels)
print('epoch %d, loss %f' % (epoch + 1, train_l.mean().item()))
train_ls.append(train_l.mean().item())
test_l = squared_loss(net(test_features),test_labels)
print('epoch %d, loss %f' % (epoch + 1, test_l.mean().item()))
test_ls.append(test_l.mean().item())
d2l.semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'loss',
range(1, num_epochs + 1), test_ls, ['train', 'test'])
对不同的参数,我们用不同的optimizer实例,w需要衰减,b不需要.
optimizer_w =torch.optim.SGD(params=[net.weight],lr=lr,weight_decay=wd) #权重衰减
optimizer_b =torch.optim.SGD(params=[net.bias],lr=lr) #偏差参数衰减
```
同样的,在更新参数时,需要对两个optimizer实例都调用
optimizer_w.step()
optimizer_b.step()
最终绘制效果如下:
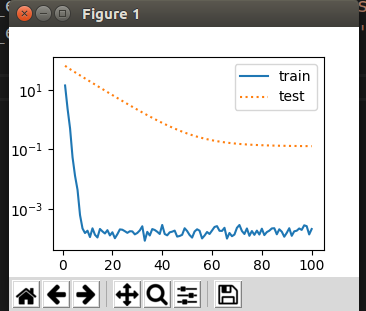从头学pytorch(六):权重衰减的更多相关文章
- 从头学pytorch(一):数据操作
跟着Dive-into-DL-PyTorch.pdf从头开始学pytorch,夯实基础. Tensor创建 创建未初始化的tensor import torch x = torch.empty(5,3 ...
- 从头学pytorch(七):dropout防止过拟合
上一篇讲了防止过拟合的一种方式,权重衰减,也即在loss上加上一部分\(\frac{\lambda}{2n} \|\boldsymbol{w}\|^2\),从而使得w不至于过大,即不过分偏向某个特征. ...
- 从头学pytorch(十六):VGG NET
VGG AlexNet在Lenet的基础上增加了几个卷积层,改变了卷积核大小,每一层输出通道数目等,并且取得了很好的效果.但是并没有提出一个简单有效的思路. VGG做到了这一点,提出了可以通过重复使⽤ ...
- 从头学pytorch(三) 线性回归
关于什么是线性回归,不多做介绍了.可以参考我以前的博客https://www.cnblogs.com/sdu20112013/p/10186516.html 实现线性回归 分为以下几个部分: 生成数据 ...
- 从头学pytorch(二) 自动求梯度
PyTorch提供的autograd包能够根据输⼊和前向传播过程⾃动构建计算图,并执⾏反向传播. Tensor Tensor的几个重要属性或方法 .requires_grad 设为true的话,ten ...
- 从头学pytorch(十二):模型保存和加载
模型读取和存储 总结下来,就是几个函数 torch.load()/torch.save() 通过python的pickle完成序列化与反序列化.完成内存<-->磁盘转换. Module.s ...
- 从头学pytorch(十九):批量归一化batch normalization
批量归一化 论文地址:https://arxiv.org/abs/1502.03167 批量归一化基本上是现在模型的标配了. 说实在的,到今天我也没搞明白batch normalize能够使得模型训练 ...
- 从头学pytorch(五) 多层感知机及其实现
多层感知机 上图所示的多层感知机中,输入和输出个数分别为4和3,中间的隐藏层中包含了5个隐藏单元(hidden unit).由于输入层不涉及计算,图3.3中的多层感知机的层数为2.由图3.3可见,隐藏 ...
- 从头学pytorch(九):模型构造
模型构造 nn.Module nn.Module是pytorch中提供的一个类,是所有神经网络模块的基类.我们自定义的模块要继承这个基类. import torch from torch import ...
随机推荐
- select筛选用户数据
- nodeJs学习-03 GET数据请求,js拆解/querystring/url
原生JS解析参数: const http = require('http'); http.createServer(function(req,res){ var GET = {}; //接收数据容器 ...
- 在 Deepin 15.9 安装 KiCad EDA 5.1 (2019-05-30)
在 Deepin 15.9 安装 KiCad EDA 5.1 Deepin (深度系统)是世界著名的 Linux 发行版. KiCad EDA 是世界最强大的开源 PCB 绘制软件. 尝试一:在深度商 ...
- Data Flow-File Read-基本过程
- uni-app获取当前位置
uniapp获取当前城市: 官方api:uni.getLocation()获取当前的地理位置.速度. 在微信小程序中,当用户离开应用后,此接口无法调用,除非申请后台持续定位权限:当用户点击“显示在聊天 ...
- Spark Steaming消费kafka数据条数变少问题
对于基于Receiver 形式,我们可以通过配置 spark.streaming.receiver.maxRate 参数来限制每个 receiver 每秒最大可以接收的记录的数据:对于 Direct ...
- python基础之包的导入
包的导入 python是一门灵活性的语言 ,也可以说python是一门胶水语言,顾名思义,就是可一导入各类的包, python的包可是说是所有语言中最多的.当然导入包大部分是为了更方便,更简便,效率更 ...
- phpstorm鼠标显示问题
https://segmentfault.com/q/1010000004319802 使用phpstorm,不知道碰到了什么键,鼠标变成了一个字符那么宽的灰色色块,原来是一根很细的竖线,怎么弄?没法 ...
- 解决Pycharm中SystemError报错
报错描述- 代码逻辑大致是, 开启线程, 监听kafka生产者push的topic消息.- 问题出现在监听过程中, 线程在接收几条topic之后出现报错, 不再处理数据12报错代码Exception ...
- H3C PPP协议的组成
