apriori关联规则

挖掘数据集：贩物篮数据
 频繁模式：频繁地出现在数据集中的模式，例如项集，子结构，子序列等
 挖掘目标：频繁模式，频繁项集，关联规则等
 关联规则：牛奶=>鸡蛋【支持度=2%，置信度=60%】
 支持度：分析中的全部事务的2%同时贩买了牛奶和鸡蛋
 置信度：贩买了牛奶的筒子有60%也贩买了鸡蛋
 最小支持度阈值和最小置信度阈值：由挖掘者戒领域专家设定

项集：项（商品）的集合
 k-项集：k个项组成的项集
 频繁项集：满足最小支持度的项集，频繁k-项集一般记为L k
 强关联规则：满足最小支持度阈值和最小置信度阈值的规则

apriori算法：

两步过程：找出所有频繁项集；由频繁项集产生强关联规则

具体挖掘步骤：

1.依据支持度找出所有频繁项集（频度）

2.依据置信度产生关联规则（强度）

原理：如果一个项集是频繁项集，那么它的所有子集也是频繁项集；按照这个原理的逆否命题——如果一个集合有不是频繁项集的子集，那么该集合一定不是频繁项集

算法工作流程（假设min_sup=2）：

候选k项集剪枝生成频繁k项集，频繁k项集自连接生成候选(k+1)项集，注意：频繁k项集自连接的前提是前(k-1)项相同，否则过滤掉该项集，不予连接，例如上图中L2*L2时，没有生成{I1,I3,I5}的原因就是{I1,I3,I5}的一个2项子集{I3,I5}没有出现在频繁2项集列表中，没有出现{I2,I3,I4}{I2,I3,I5}的原因也在这里，连接这步是算法优化的重点，另外一个技巧是增大min_sup，过滤掉相当一部分项集，否则自连接生成的项集会撑爆内存。具体步骤说明如下：

步骤说明
 扫描D，对每个候选项计数，生成候选1-项集C1
 定义最小支持度阈值为2，从C1生成频繁1-项集L1
 通过L1xL1生成候选2-项集C2
 扫描D，对C2里每个项计数，生成频繁2-项集L2
 计算L3xL3，利用apriori性质：频繁项集的子集必然是频繁的，我们可以删去一部分项
，从而得到C3，由C3再经过支持度计数生成L3
 可见Apriori算法可以分成 连接，剪枝（1.扫描事务，去掉小于min_sup的项；2.去掉其子集不是频繁项集的项集） 两个步骤不断循环重复

由频繁项集提取关联规则：

例如：计算出的频繁项集{I1,I2,I5}，提取规则步骤如下：

Apriori算法的瓶颈：

1.通过笛卡尔积自连接产生的组合项过多（只能人为提高min_sup减少频繁项集数目，这是以牺牲精度为代价的）；

2.每次剪枝都需要去扫描事务数据库，而事务数据库包含难以计数之多的购物篮信息

总之：海量数据下，Apriori算法的时空复杂度都不容忽视。

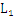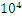空间复杂度：如果数量达到的量级，那么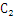中的候选项将达到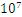的量级。

时间复杂度：每计算一次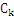就需要扫描一遍数据库。