傅里叶：有关FFT,DFT与蝴蝶操作（转 重要！！！！重要！！！！真的很重要！！！！）

转载地址：http://blog.renren.com/share/408963653/15068964503（作者 :  徐可扬）

有没有！！！

其实我感觉这个学期算法最难最搞不懂的绝对不是动态规划啊！绝对是快速傅里叶变换啊！最近才弄懂有木有。

有不少人问我，于是干脆就写成日志吧。

首先明确一下基本概念吧，就三点，DFT,FFT,蝴蝶操作。

DFT（离散傅里叶变换）：书上写的最清楚的一句话叫做，向量y=(y0,y1,……yn-1)是系数向量a=(a0,a1,,……,an-1)的离散傅里叶变换，也写作y=DFTn(a)。说白了，就是求n个y值，但是n个自变量x的取值很特殊

FFT(快速傅里叶变换)：这个名词好理解，就是很快地算出这n个y值。一般我们计算n个n次的多项式值需要O(n^2)的时间。现在用FFT可以减少到O(n*logn)。具体原理一两句话说不完……要考的话也太理论性了…

蝴蝶操作:这个应该是让大家最费解的…他就是一个FFT得实际应用…因为这是实践的东西所以要掌握。书上有一个图，虽然感觉看书不一定看的怎么懂，但是这个图还是要记住。不过我觉得从下往上写看起来更舒服。

转过来以后，向左边是加，向右边是减。谨记啊！

突然发现好难解释，先把宋老师课件里面上次坑爹的没有答案的课后练习拿来看看。

我这里a0,a1,a2……就不调换顺序了，其实是一样的，格式不同罢了。

a=(0,1)

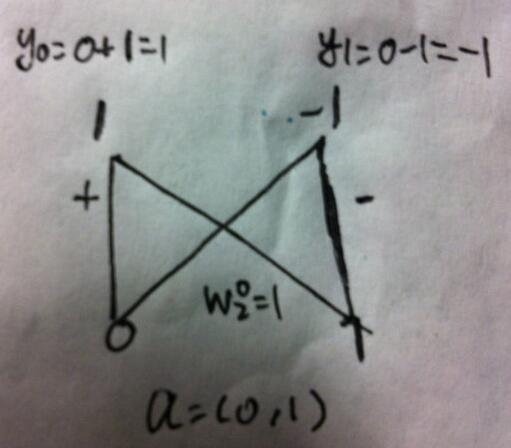
经过FFT，Y=（1，-1），这个就是书上最简单的应用了。

再来一个简单的 a=(1,0).

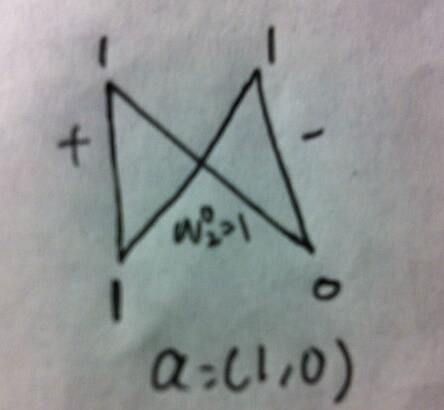
y=(1,1).

我觉得要考试一般就是考四个的吧，两个太简单了，8个的太复杂了（我后面有写）

例子

a=(1,1,0,1)

y=(3,1,-1,1)  注意算出来是 y0,y2,y1,y3的顺序。

a=(0,1,2,3)

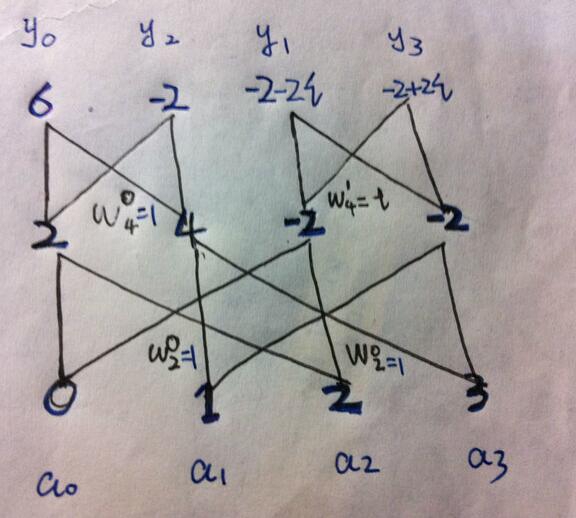
y=（6，-2-2i,  -2 , -2+2i）.

注意右上角的蝶形运算中的旋转因子变成了(恩！？怎么不能插公式啊！)w(1/4）=i。。。那是因为在a0,a2的蝶形运算中我们多乘了(n/2)，这里n=2.（这个我解释不来…不过这个数是固定的，背就行了）。

那我上个八个的，有点复杂，估计可能不会考

a=(0,1,2,3,4,5,6,7).

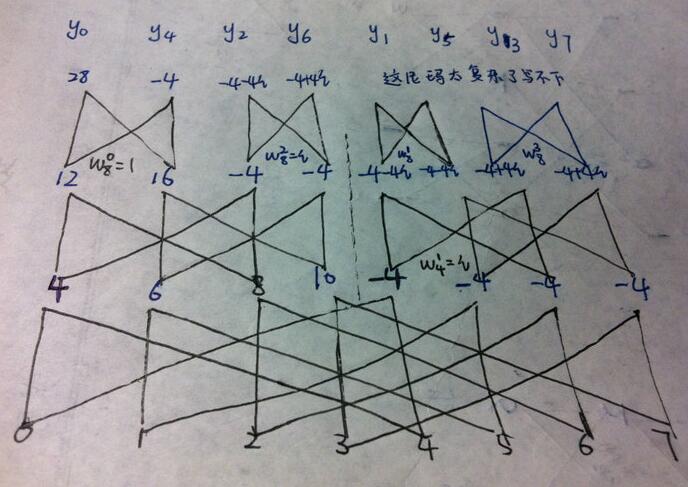
y的顺序如图

告诉大家一个比较好的办法判断是否算对了，直接人肉使用O(n^2)算法就好了，举四个的例子。就是把x得值带入多项式y=a3*x^3+a2*x^2+a1*x+a0算出y值什么的。x0=1,x1=i，x2=-1,x3=-i带入。这样的话，其实考察算没算对完全是个伪命题吗……

再提醒一次，左加右减哦！

最后再说一下这玩意有什么用，什么信号学的废话就不说了。无非是FFT用N*LogN时间算出点值方便用点值法算出多项式乘法的系数结果，这个大家看书上510的图我觉得就能理解了。插值神马的，背公式吧……虽然我也不记得了。

时间有点紧迫，感觉写的巨烂无比，大神们如果发现写错了留言给我立马改，关键不要误人子弟……

这有帮助的请让我知道。感谢大家!

If it helps you , let me know. Thank you !