网络最大流的（Edmond Karp）算法

容量网络：在有向图D=（V，A），指定一个点为发点，记作 s，指定另一个点为收点，记作 t，其余点叫作中间点。对于A的每条弧（Vi,Ai），都对应一个权数 C ≥0，称为弧（Vi , Ai）的容量，将这样的赋权有向图叫作一个容量网络，记作D=（V,A,C）。

这有点不好懂，我解释一下网络最大流的意思是，从s（源点）到t（汇点）需要通过n条路径也有可能有一条s和t直接相连的，每一条路径能通过的最大流量（容量网络）又不尽相同，我们要求的是从s到t的最大流量，如图：

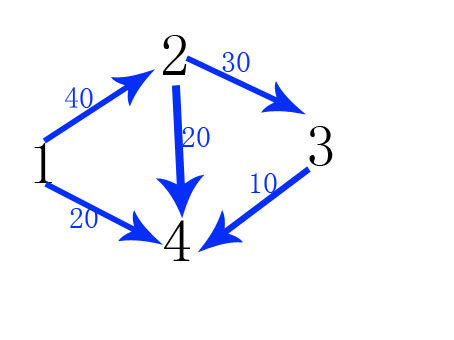
从1到4的路径有：(1)1—>4;(2)1—>2—>4;(3)1-->2-->3-->4

（1）的最大流量显然是20；（2）的最大流量是20;（3）的最大流量是10；

因为20+10+10（三条路径最大流量）<20+40（从1出发的最大流量）；所以根据此图可以找到1到4的最大流为20+10+10=50；

#include <iostream>
#include <stdio.h>
#include <algorithm>
#include <string.h>
#include <queue>
using namespace std;
const int MAX=;
int map[][],flow[],pre[],n,m;
bool vis[];
int BFS()
{
    int up;
    queue<int> q;
    vis[]=;
    memset(pre,-,sizeof(pre));
    memset(vis,,sizeof(vis));
    for(int i=;i<=n;i++)
        flow[i]=MAX;
    q.push();
    while(!q.empty())
    {
       up=q.front();
        q.pop();
        if(up==n)
            break;
        for(int i=;i<=n;i++)
        {
            if(!vis[i]&&map[up][i]>)
            {
                vis[i]=;
                flow[i]=min(flow[up],map[up][i]);
                pre[i]=up;
                q.push(i);
            }
        }
    }
    if(!vis[n]||n==)
        return -;
    return flow[n];
}
int EK()
{
    int d,maxflow=,up,down;
    maxflow=;
    while((d=BFS())!=-)
    {
        maxflow+=d;
        down=n;
        while(down!=)
        {
            up=pre[down];
            map[up][down]-=d;
            map[down][up]+=d;
            down=up;
        }
    }
    return maxflow;
}
int main()
{
    int T,a,b,c,h=,i;
    scanf("%d",&T);
    while(T--)
    {
        memset(map,,sizeof(map));
        scanf("%d%d",&n,&m);
        for(i=;i<=m;i++)
        {
            scanf("%d%d%d",&a,&b,&c);
            map[a][b]+=c;
        }
        printf("Case %d: %d\n",h++,EK());
    }
    return ;
}