Bellman - Ford 算法解决最短路径问题

Bellman - Ford 算法:

一:基本算法

　　对于单源最短路径问题,上一篇文章中介绍了 Dijkstra 算法,但是由于 Dijkstra 算法局限于解决非负权的最短路径问题,对于带负权的图就力不从心了,而Bellman - Ford算法可以解决这种问题.

　　Bellman - Ford 算法可以处理路径权值为负数时的单源最短路径问题.设想可以从图中找到一个环路且这个环路中所有路径的权值之和为负.那么通过这个环路,环路中任意两点的最短路径就可以无穷小下去.如果不处理这个负环路,程序就会永远运行下去.Bellman -Ford 算法具有分辨这种负环路的能力.

　　Bellman - Ford算法基于动态规划,反复用已有的边来更新最短距离,Bellman - Ford算法的核心就是松弛.对于点 v 和 u,如果 dist[u] 和 dist[v] 不满足 dist[v] <= dist[u] + map[u][v],那么dist[v] 就应该被更新为 dist[u] + map[u][v].反复地利用上式对每条边进行松弛,从而更新 dist[] 数组,如果没有负权回路的话,应当会在 n - 1 次松弛之后结束算法.原因在于考虑对每条边进行 1 次松弛的时候,得到的实际上是至多经过 0 个点的最短路径(初始化每个点到源点的距离为无穷,这里的经过 0 个点意思为路径仅由源点和终点组成),对每条边进行两次松弛的时候得到的至多是经过 1 个点的最短路径,如果没有负权回路,那么任意两点的最短路径至多经过 n - 2 个点(不包含源点和终点这两个点),因此经过 n - 1 次松弛操作后应当可以得到最短路径.如果有负权回路,那么第 n 次松弛操作仍然会成功(即第 n 次松弛仍然存在一条边可以对其进行松弛操作),但是不存在负权回路的图应该在第 n - 1 次松弛之后,已经不存在可以松弛的边了,所以Bellman -Ford算法就利用了这个性质以达到判定负环的目的.

二:伪代码

　　在以下说明中: s 为源, map[][] 记录图的信息,map[u][v] 为点 u 到点 v 的边的长度,如果 u 和 v 之间不存在边那么 map[u][v] = INF, 结果保存在 dist[]数组里:

　　(1):初始化,所有点 i 赋初值 dist[i] = INF, 出发点为 s, dist[s] = 0.

　　(2):对于每条边<u, v>,如果 dist[u] != INF, 且 dist[v] > dist[u] + map[u][v],则 dist[v] = map[u] + map[u][v].

　　(3):循环步骤(2)  n - 1 次或直到某次循环中不再更新,进入步骤(4).

　　(4):对于每条边<u, v>, 如果 dist[u] != INF, 且dist[v] > dist[u] + map[u][v],则存在负权回路.

for i =  to n -  {
　　for each v in G(V, E) {
      　　  for each edge<v, u> in E {
      　　        RELAX<v, u>;
      　　 }
　　}
}

 三:以图为例

初始化图, dist[i]代表当前点 i 距离源点 “5” 的最短距离, 图中存在两调负权边,但不存在负环,红色的点代表源点,红色的边代表正在松弛的边,绿色的点代表正在松弛的边的起点,蓝色的点代表正在松弛的边的终点:

第一次循环:

(从点 “1” ～ 到点 "6" 选择 dist[i] != INF 的点):

第一个选中的点为 “5”,则对从点 “5” 出发的所有边进行松弛操作:

由于之后没有了可以选择的点了,所以第一次循环结束.

第二次循环:

(从点 “1” ～ 到点 "6" 选择 dist[i] != INF 的点):

第一个选中的点为 “3”,则对从点 “3” 出发的所有边进行松弛操作:

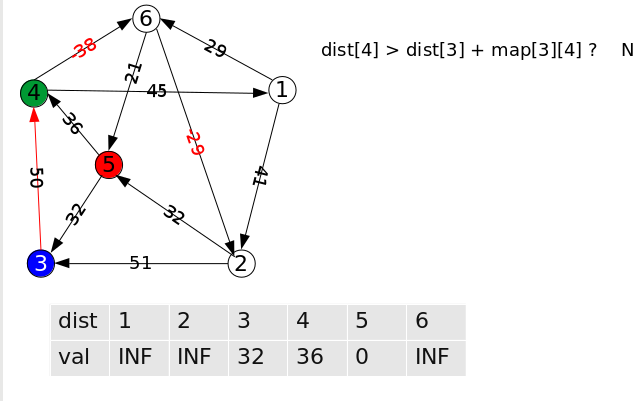
第二个选中的点为点 “4”,对所有从点 “4” 出发的所有边进行松弛:

第三个选中的点为点 “5”,这里很显然可以看出,边<"5", "4"> 和边 <"5", "3">不用进行松弛.

第四个选中的点为点 “6”,然后依次尝试对边<"6", "2"> <"6", "5">进行松弛:

到这里,第二次循环结束.

第三次循环:

(从点 “1” ～ 到点 "6" 选择 dist[i] != INF 的点):

第一个选中的点为 “1”,则对从点 “1” 出发的所有边进行松弛操作:

第二个选中的点为点 “2”,则对所有从点 “2”出发的所有尝试松弛操作:

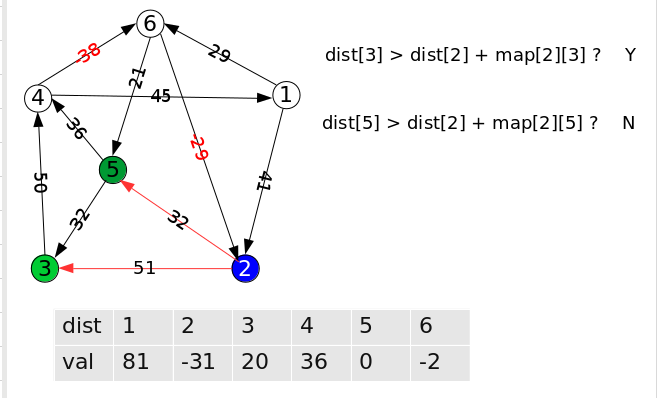
第三个选中的点为点 “3”,尝试对所有从 点“3”出发的边进行松弛,可以很清楚看到边 <"3", "4">无法松弛,dist[4] <= dsit[3] + map[3][4]成立.

第四个选中的点为点 “4”,尝试对所有从 点“4”出发的边进行松弛:

第五个选中的点为点 “5”,尝试对所有从点 “5” 出发的边进行松弛,也可以很清楚看到,边<"5", "4"> 和边 <"5", "3">不用进行松弛.

第六个选中的点为点 “6”,尝试对所有从点 “6” 出发的边进行松弛:

至此第三次已经结束.

第四次循环:

(从点 “1” ～ 到点 "6" 选择 dist[i] != INF 的点):

选择点 “1”.......

选择点 “2”.......

选择点 “3”.......

选择点 “4”.......

选择点 “5”.......

选择点 “6”.......

执行完第四次循环,会发现所有的边都未再次进行松弛,事实上算法至此已经求出源点到其他各顶点的最短路径,此时算法应该结束.

最后的最短路经为:

 四:代码

使用链式前向星存图的信息:

 const int INF = ;
 const int MAXN =;
 const int MAXE =;
 int dist[MAXN + ];//dist[i]表示点 i 到源点的最短距离

 int head[MAXN + ];//链式前向星用于存图
 struct NODE { int to; int w; int next; };
 NODE edge[MAXE + ];

 bool BellmanFord(int n, int s) {// s 为源点
     for(int i = ; i <= n; i++) dist[i] = INF;//初始化
     dist[s] = ;
     for(int i = ; i < n - ; i++) {//对于所有边循环 n - 1,即尝试松弛 n - 1 次
         for(int j = ; j <= n; j++) { //选取一个起点
             if(dist[j] == INF) continue;
             for(int k = head[j]; k != -; k = edge[k].next) { //遍历从当前起点出发的所有边,并尝试进行松弛
                 if(edge[k].w != INF && dist[edge[k].to] > dist[j] + edge[k].w) {//进行松弛操作
                     dist[edge[k].to] = dist[j] + edge[k].w;
                 }
             }
         }
     }
     for(int j = ; j <= n; j++) {//进行第 n 次松弛 判断是否存在负环
         for(int k = head[j]; k != -; k = edge[k].next) { //存在负环返回 false
             if(edge[k].w != INF && dist[edge[k].to] > dist[j] + edge[k].w) return false;
         }
     }
     return true;
 }

参考《图论及应用》和网上部分资料.