K均值聚类和代码实现
K均值聚类是一种无监督学习分类算法。
介绍
对于$n$个$m$维特征的样本,K均值聚类是求解最优化问题:
$\displaystyle C^*=\text{arg}\min\limits_{C}\sum\limits_{l = 1}^K\sum\limits_{x\in C_l}||x-x_l||^2$
其中$C$表示某种样本的划分方式,$x\in C_l$表示被划分在第$l$类的样本,$x_l$表示被划分在第$l$类的所有样本的中心,也就是均值。所以上式表示最小化所有类别内样本到其对应的类别样本均值的距离之和。最优化这个问题是NP难问题,所以现实采用类似贪心的迭代算法来逼近最优解(不一定最优)。具体流程如下(每个样本只能属于一个类别):
0、初始化$K$个类的均值为随机$m$维向量。
1、将每个样本划分到与之距离最小的类别均值对应的类别中。
2、根据划分进的样本,每个类别重新计算类别均值,并记录。
3、比较连续两次的类别均值,如果差别小于一定阈值就结束,否则回到1。
通过计算可以知道时间复杂度是$O(mnk)$。
代码实现
Numpy手动实现
首先使用由正态分布生成的两簇点集来实验,每个簇各200个点。可能由于这两个点集比较靠近,所以分类完全错误,如图:

重新生成5簇正态分布点集,这次每个集合之间相对较远,除了少数没有正确聚类外(两类交汇处),表现不错:
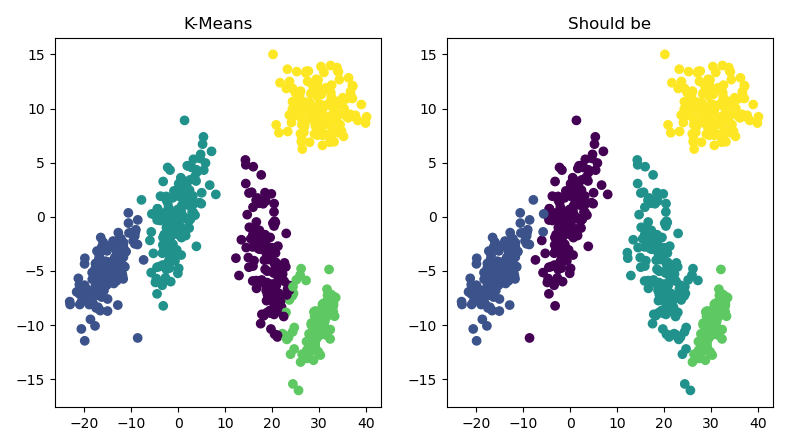
代码如下:
#%%获取数据
import matplotlib.pyplot as plt
import numpy as np
import xlrd table = xlrd.open_workbook('test.xlsx').sheets()[0]#读取Excel数据
data = []
for i in range(0,table.nrows):#假设第一行是表头不读入
data.append(table.row_values(i))
data = np.array(data)
#%%聚类
def distance(a,b):
d = a-b
return np.dot(d,d)
def clusterize(data,class_m):#关于类均值对样本分类
for i in data:
min_dis = np.inf
for j in range(len(class_m)):
t = distance(i[:-1],class_m[j])
if t<min_dis:
min_dis=t
i[-1]=j def calc_mean(data,class_m):#以类中样本计算均值
class_m -= class_m
num = np.zeros([len(class_m)])
for i in data:
num[int(i[-1])]+=1
class_m[int(i[-1])]+=i[:-1]
for i in range(len(class_m)):
class_m[i]/=num[i]
def updated_mean(dif):#计算前后两次更新的均值距离,传入前后差值
sum_ = 0
for i in dif:
sum_ += np.dot(i,i)
return sum_
def k_means_cluster(data,K):
class_mean = data[0:K,:-1]
class_mean_old = -class_mean
t = updated_mean(class_mean-class_mean_old)
ii = 0
while t>0.0001:
class_mean_old = class_mean.copy()
clusterize(data,class_mean)
print(class_mean)
print(class_mean_old)
calc_mean(data,class_mean)
print(class_mean)
print(class_mean_old)
t = updated_mean(class_mean-class_mean_old)
print(t)
ii+=1
print(ii)
data1 = data.copy()
np.random.shuffle(data1)
k_means_cluster(data1,5) #要分几类直接这里设置################################## #%%绘制结果
import matplotlib.pyplot as plt fig = plt.figure()
ax1 = fig.add_subplot(121)
ax2 = fig.add_subplot(122)
ax1.scatter(data1[:,0],data1[:,1],c = data1[:,-1])
ax1.set_title("K-Means")
ax2.scatter(data[:,0],data[:,1],c = data[:,-1])
ax2.set_title("Should be")
plt.show()
Sklearn
使用封装好的Sklearn,代码如下:
#%%获取数据
import matplotlib.pyplot as plt
import numpy as np
import xlrd table = xlrd.open_workbook('test.xlsx').sheets()[0]#读取Excel数据
data = []
for i in range(0,table.nrows):#假设第一行是表头不读入
data.append(table.row_values(i))
data = np.array(data)
#%%聚类
from sklearn.cluster import KMeans kmeans = KMeans(n_clusters=5)
kmeans.fit(data[:,:-1])
y = kmeans.predict(data[:,:-1])
fig = plt.figure()
ax1 = fig.add_subplot(121)
ax1.scatter(data[:,0],data[:,1],c = y)
ax1.set_title("K-Means")
ax2 = fig.add_subplot(122)
ax2.scatter(data[:,0],data[:,1],c=data[:,-1])
ax2.set_title("Should be")
plt.show()
结果图:
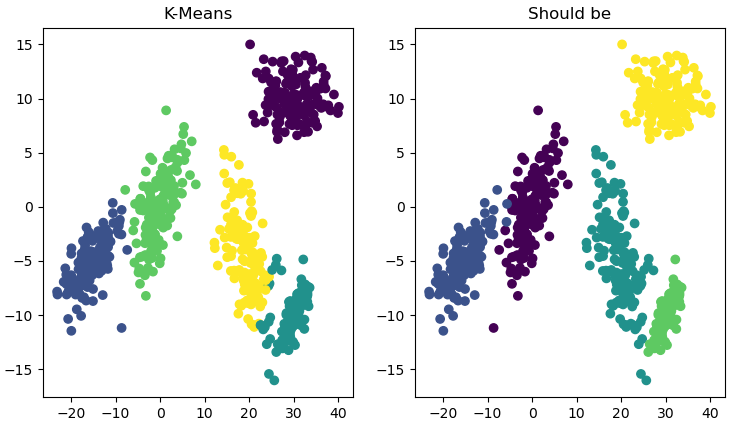
K均值聚类和代码实现的更多相关文章
- 5-Spark高级数据分析-第五章 基于K均值聚类的网络流量异常检测
据我们所知,有‘已知的已知’,有些事,我们知道我们知道:我们也知道,有 ‘已知的未知’,也就是说,有些事,我们现在知道我们不知道.但是,同样存在‘不知的不知’——有些事,我们不知道我们不知道. 上一章 ...
- 机器学习实战5:k-means聚类:二分k均值聚类+地理位置聚簇实例
k-均值聚类是非监督学习的一种,输入必须指定聚簇中心个数k.k均值是基于相似度的聚类,为没有标签的一簇实例分为一类. 一 经典的k-均值聚类 思路: 1 随机创建k个质心(k必须指定,二维的很容易确定 ...
- Python实现kMeans(k均值聚类)
Python实现kMeans(k均值聚类) 运行环境 Pyhton3 numpy(科学计算包) matplotlib(画图所需,不画图可不必) 计算过程 st=>start: 开始 e=> ...
- 机器学习理论与实战(十)K均值聚类和二分K均值聚类
接下来就要说下无监督机器学习方法,所谓无监督机器学习前面也说过,就是没有标签的情况,对样本数据进行聚类分析.关联性分析等.主要包括K均值聚类(K-means clustering)和关联分析,这两大类 ...
- ML: 聚类算法-K均值聚类
基于划分方法聚类算法R包: K-均值聚类(K-means) stats::kmeans().fpc::kmeansruns() K-中心点聚类(K-Medoids) ...
- 机器学习算法与Python实践之(六)二分k均值聚类
http://blog.csdn.net/zouxy09/article/details/17590137 机器学习算法与Python实践之(六)二分k均值聚类 zouxy09@qq.com http ...
- 机器学习之路:python k均值聚类 KMeans 手写数字
python3 学习使用api 使用了网上的数据集,我把他下载到了本地 可以到我的git中下载数据集: https://github.com/linyi0604/MachineLearning 代码: ...
- k均值聚类算法原理和(TensorFlow)实现
顾名思义,k均值聚类是一种对数据进行聚类的技术,即将数据分割成指定数量的几个类,揭示数据的内在性质及规律. 我们知道,在机器学习中,有三种不同的学习模式:监督学习.无监督学习和强化学习: 监督学习,也 ...
- SciPy k均值聚类
章节 SciPy 介绍 SciPy 安装 SciPy 基础功能 SciPy 特殊函数 SciPy k均值聚类 SciPy 常量 SciPy fftpack(傅里叶变换) SciPy 积分 SciPy ...
- 聚类之K均值聚类和EM算法
这篇博客整理K均值聚类的内容,包括: 1.K均值聚类的原理: 2.初始类中心的选择和类别数K的确定: 3.K均值聚类和EM算法.高斯混合模型的关系. 一.K均值聚类的原理 K均值聚类(K-means) ...
随机推荐
- 安装 AWS CLI
安装 macOS 使用 Homebrew: brew install awscli 手动安装: curl "https://awscli.amazonaws.com/AWSCLIV2.pkg ...
- 【YashanDB知识库】服务端是GBK编码,导致从22.2.12.100升级到22.2.13.100失败问题
问题现象 问题单:22.2.12.100升级到22.2.13.100失败 现象:如下图,从22.2.12.100升级到22.2.13.100失败,报错. 问题风险及影响 版本升级失败,影响上线 问题发 ...
- webpack笔记-webpack基础用法(二)
webpack 本质上是一个打包工具,它会根据代码的内容解析模块依赖,帮助我们把多个模块的代码打包. 一切文件:JavaScript.CSS.SCSS.图片.模板,在 Webpack 眼中都是一个个模 ...
- OCR技术的昨天今天和明天!2023年最全OCR技术指南!
OCR是一项科技革新,通过自动化大幅减少人工录入的过程,帮助用户从图像或扫描文档中提取文字,并将这些文字转换为计算机可读格式.这一功能在许多需要进一步处理数据的场景中,如身份验证.费用管理.自动报销. ...
- 系统编程-进程-探究父子进程的数据区、堆、栈空间/ 当带缓存的C库函数遇上fork
1. test1 #include <stdio.h> #include <unistd.h> #include <stdlib.h> /******全局变量位于数 ...
- 搭建本地nginx-rtmp服务,初体验rtmp推流、拉流
实验环境说明: ubuntu 16.04 进行本实验的前提:需要在ubuntu上搭建好ffmpeg环境,参考我的另一篇博文 ffmpeg编译过程经历的99八十一难 下面开始本文内容 PART1 编译安 ...
- java爬取航班实时数据
使用jsoup获取航班实时数据 优先使用携程航班数据 如果携程航班数据返回为空 则使用去哪儿航班信息 pom.xml <dependency> <groupId>org.js ...
- Windows 10 LTSC 2019(1809) WSL 安装 CentOS 7
1.安装WSL 通过控制面板--程序和功能--启用或关闭WIndows功能,勾选"适用于Linux的Windows子系统". 或者通过管理员权限打开 PowerShel ...
- 我们如何在 vue 应用我们的权限
权限可以分为用户权限和按钮权限: 用户权限,让不同的用户拥有不同的路由映射 ,具体实现方法: 1. 初始化路由实例的时候,只把静态路由规则注入 ,不要注入动态路由规则 : 2. 用户登录的时候,根据返 ...
- 18 . 介绍一下 Promise
Promise 是js内置的构造函数,也叫做期约函数 ,它有 3 种状态 ,等待状态 pending ,成功状态 fullfilled ,失败状态 reject :2 个过程, 等待状态到成功状态 会 ...
