2018-2019 9th BSUIR Open Programming Championship

I. Equal Mod Segments

\(1 \leq n \leq 1e5\)

\(1 \leq a_i \leq 3e5\)

题解：ST表 + 扫描线 + 二维偏序

• 取模存在一个不错的性质：\(x \%p\)要么\(x\)不变，要么\(x\)至少整除\(2\)

• 所以我们考虑固定左端点\(l\)，存在\(log\ a_l\)段区间，使得右端点\(r\)在每段区间\([p,q]\)内\(a_l\ mod\ a_{l + 1}...mod\ a_r,r\in[p,q]\)不变

• 我们可以通过\(ST\)表+二分来预处理所有固定左端点和固定右端点的区间，并将所有模数相同的区间放入同一个\(vector\)中，预处理复杂度 \(O(nlog^2n)\)

• 那么我们考虑区间\([l,r]\)满足什么条件，才能对答案产生贡献

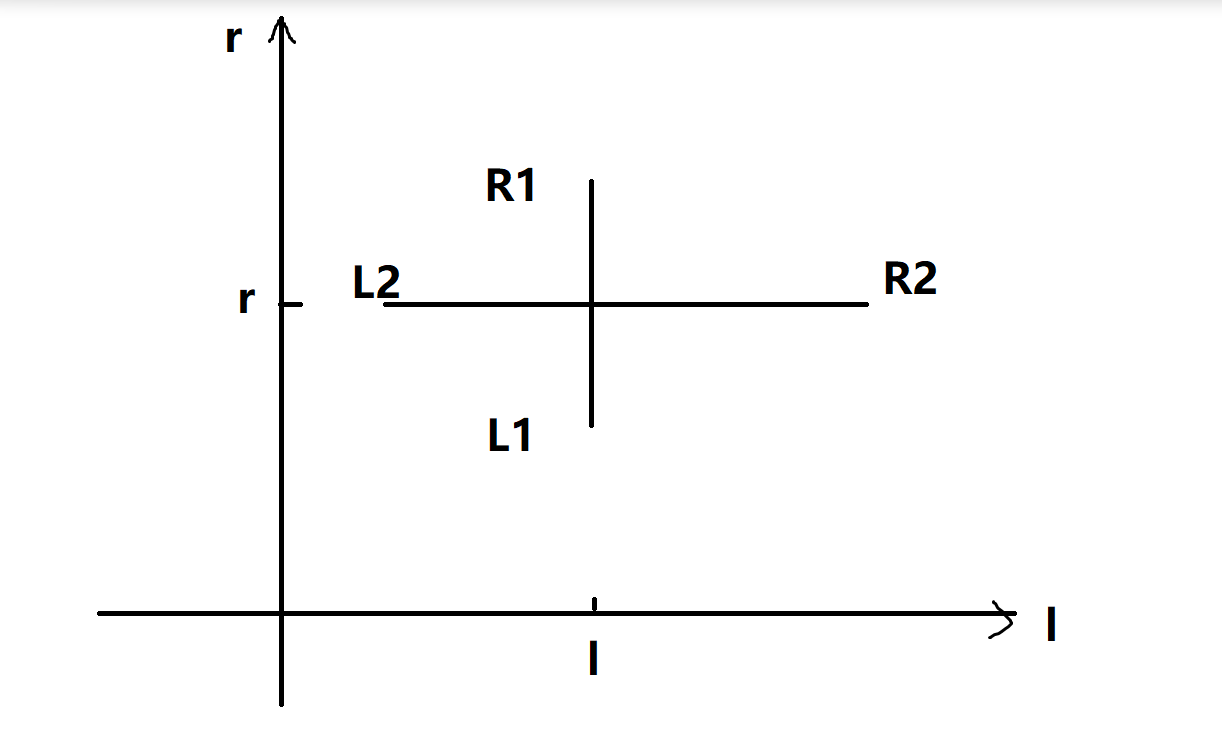
• 我们设对于\(l\)来说，模数为\(p\)的右端点\(r\)所在区间为\([L_1,R_1]\)，对于\(r\)来说，模数为\(p\)的左端点\(l\)所在区间为\([L_2,R_2]\)，那么只要保证\(L_1\leq r \leq R_1 \and L_2\leq l \leq R_2\)，那么区间\([l,r]\)就能对答案产生贡献

• 我们把条件抽象到二维平面上，横坐标为\(l\)，纵坐标为\(r\)，可以得到：

• 所以我们只要对每个模数的\(vector\)跑一次扫描线即可，扫描\(x\)轴，线段树维护\(y\)轴，求交点数量即可

const int N = 3e5 + 10, M = 4e5 + 10;

int n, a[N], st[N][18], lg2[N];
vector<array<int, 4>> vec[N];

struct info
{
    int sum;
    friend info operator+(const info &a, const info &b)
    {
        info c;
        c.sum = a.sum + b.sum;
        return c;
    }
};
struct SEG
{
    info val;
} seg[N << 2];

void up(int id)
{
    seg[id].val = seg[lson].val + seg[rson].val;
}

void change(int id, int l, int r, int x, int val)
{
    if (l == r)
    {
        seg[id].val.sum += val;
        return;
    }
    int mid = l + r >> 1;
    if (x <= mid)
        change(lson, l, mid, x, val);
    else
        change(rson, mid + 1, r, x, val);
    up(id);
}

info query(int id, int l, int r, int ql, int qr)
{
    if (ql <= l && r <= qr)
        return seg[id].val;
    int mid = l + r >> 1;
    if (qr <= mid)
        return query(lson, l, mid, ql, qr);
    else if (ql > mid)
        return query(rson, mid + 1, r, ql, qr);
    else
        return query(lson, l, mid, ql, qr) + query(rson, mid + 1, r, ql, qr);
}

void build()
{
    for (int i = 1; i <= n; ++i)
        st[i][0] = a[i];
    for (int i = 2; i <= n; ++i)
        lg2[i] = lg2[i >> 1] + 1;
    for (int j = 1; j <= 15; ++j)
        for (int i = 1; i + (1ll << j) - 1 <= n; ++i)
            st[i][j] = min(st[i][j - 1], st[i + (1ll << (j - 1))][j - 1]);
}

int query(int l, int r)
{
    if (l > r)
        return INF;
    int len = lg2[r - l + 1];
    return min(st[l][len], st[r - (1ll << len) + 1][len]);
}

void solve()
{
    cin >> n;
    int m = 0;
    for (int i = 1; i <= n; ++i)
    {
        cin >> a[i];
        m = max(m, a[i]);
    }
    build();
    for (int i = 1; i <= n; ++i)
    {
        int now = a[i];
        for (int j = i, l, r; j <= n; j = r + 1)
        {
            l = j, r = n;
            while (l <= r)
            {
                int mid = l + r >> 1;
                if (query(j + 1, mid) > now)
                    l = mid + 1;
                else
                    r = mid - 1;
            }
            vec[now].push_back({0, i, j, r});
            if (r + 1 <= n)
                now %= a[r + 1];
        }
    }
    for (int i = n; i >= 1; --i)
    {
        int now = a[i];
        for (int j = i, l, r; j >= 1; j = l - 1)
        {
            l = 1, r = j;
            while (l <= r)
            {
                int mid = l + r >> 1;
                if (query(mid, j - 1) > now)
                    r = mid - 1;
                else
                    l = mid + 1;
            }
            vec[now].push_back({1, i, l, j});
            if (l - 1 >= 1)
                now %= a[l - 1];
        }
    }
    int ans = 0;
    for (int i = 0; i <= m; ++i)
    {
        if (vec[i].empty())
            continue;
        vector<array<int, 4>> evt;
        for (auto [op, k, l, r] : vec[i])
        {
            if (op == 0) // 查询
                evt.push_back({k, 0, l, r});
            else
            {
                evt.push_back({l, -1, k, 1}); // 添加贡献
                evt.push_back({r, 1, k, -1}); // 删除贡献
            }
        }
        // 扫描线
        sort(all(evt));
        for (auto [y, op, l, r] : evt)
        {
            if (op == 0)
                ans += query(1, 1, n, l, r).sum;
            else
                change(1, 1, n, l, r);
        }
    }
    cout << ans << endl;
}

K. Innovations

题解：树链剖分 + 势能线段树

• 考虑到根号的性质，所以显然势能线段树维护\(dfs\)序
• 我们考虑每条边对答案产生的贡献为\(sz[v] \times (n - sz[v]),sz[v]为v的子树大小\)
• 设边权为\(w[v]\)，每条边的贡献为\(p[v]\)，那么每条边对答案的贡献为\(w[v] \times p[v]\)，所以我们线段树直接维护答案，如果该区间不全为\(1\)就暴力递归到叶子节点进行修改

const int N = 2e5 + 10;
const int mod = 1e9 + 7;

int n, m, sz[N], p[N], dep[N], top[N], hson[N], l[N], r[N], fa[N], w[N], idx, mp[N];
vector<pair<int, int>> g[N];

void dfs1(int u, int par)
{
    fa[u] = par;
    dep[u] = dep[par] + 1;
    sz[u] = 1;
    hson[u] = -1;
    for (auto [v, val] : g[u])
    {
        if (v == par)
            continue;
        dfs1(v, u);
        sz[u] += sz[v];
        w[v] = val;
        p[v] = sz[v] * (n - sz[v]);
        if (hson[u] == -1 || sz[v] > sz[hson[u]])
            hson[u] = v;
    }
}

void dfs2(int u, int head)
{
    top[u] = head;
    l[u] = ++idx;
    mp[idx] = u;
    if (hson[u] != -1)
        dfs2(hson[u], head);
    for (auto [v, val] : g[u])
    {
        if (v == fa[u])
            continue;
        if (v == hson[u])
            continue;
        dfs2(v, v);
    }
    r[u] = idx;
}

struct info
{
    int sum, flag; // flag 代表区间是否全为 1
    friend info operator+(const info &a, const info &b)
    {
        info c;
        c.sum = (a.sum + b.sum) % mod;
        c.flag = a.flag && b.flag;
        return c;
    }
    info(int sum = 0, int flag = 0) : sum(sum), flag(flag) {}
};
struct SEG
{
    int lazy;
    info val;
} seg[N << 2];

void up(int id)
{
    seg[id].val = seg[lson].val + seg[rson].val;
}

void build(int id, int l, int r)
{
    if (l == r)
    {
        if (mp[l] == 1)
        {
            seg[id].val = info(0, 1);
            return;
        }
        if (w[mp[l]] == 1)
            seg[id].val = info(w[mp[l]] * p[mp[l]], 1);
        else
            seg[id].val = info(w[mp[l]] * p[mp[l]], 0);
        return;
    }
    int mid = l + r >> 1;
    build(lson, l, mid);
    build(rson, mid + 1, r);
    up(id);
}

void modify(int id, int l, int r, int ql, int qr)
{
    if (ql <= l && r <= qr && seg[id].val.flag)
        return;
    if (l == r)
    {
        w[mp[l]] = (int)(sqrt(w[mp[l]]));
        if (w[mp[l]] == 1)
            seg[id].val.flag = 1;
        else
            seg[id].val.flag = 0;
        seg[id].val.sum = w[mp[l]] * p[mp[l]];
        return;
    }
    int mid = l + r >> 1;
    if (qr <= mid)
        modify(lson, l, mid, ql, qr);
    else if (ql > mid)
        modify(rson, mid + 1, r, ql, qr);
    else
    {
        modify(lson, l, mid, ql, qr);
        modify(rson, mid + 1, r, ql, qr);
    }
    up(id);
}

void solve()
{
    cin >> n >> m;
    for (int i = 1; i < n; ++i)
    {
        int u, v, w;
        cin >> u >> v >> w;
        g[u].push_back({v, w});
        g[v].push_back({u, w});
    }
    dfs1(1, 0);
    dfs2(1, 1);
    build(1, 1, n);
    cout << seg[1].val.sum << endl;
    while (m--)
    {
        int u, v;
        cin >> u >> v;
        while (top[u] != top[v])
        {
            if (dep[top[u]] > dep[top[v]])
            {
                modify(1, 1, n, l[top[u]], l[u]);
                u = fa[top[u]];
            }
            else
            {
                modify(1, 1, n, l[top[v]], l[v]);
                v = fa[top[v]];
            }
        }
        if (dep[u] > dep[v] && l[v] + 1 <= l[u])
            modify(1, 1, n, l[v] + 1, l[u]);
        else if (dep[u] < dep[v] && l[u] + 1 <= l[v])
            modify(1, 1, n, l[u] + 1, l[v]);
        cout << seg[1].val.sum << endl;
    }
}