洛谷 NOIP 2023 模拟赛 T2 汪了个汪

洛谷 NOIP 2023 模拟赛 T2 汪了个汪

考试建出正解图不知道怎么处理，题解区樱雪喵博客薄纱。

樱雪喵题解链接

Ps:笔者语文爆炸，不建议阅读本文

思路

首先你会发现，一共有 \(\frac{n(n-1)}{2}\) 个二元组，有 \(\frac{n(n-1)}{2}\) 个横向相邻数对。

按照题目要求，一个横向数对对应一个二元组。

你又发现（但是我没发现）刚好有 \(n-1\) 个差为 1 的二元组，有 \(n-2\) 个差为 2 的二元组……

接着又有，第 \(i\) 行刚好要放 \(i-1\) 个二元组。

刚好对应上！（这简直比巧克力还要巧）

那是不是把差为 \(i\) 的二元组，放到第 \(n-i+1\) 行就好了呢？

你会发现 \((1,4),(2,5),(3,6)\) 这种东西根本放不到一行。

考虑一下，把这个金字塔转动一下：

如 \(n=5\) 时，从这样：

变成这样：

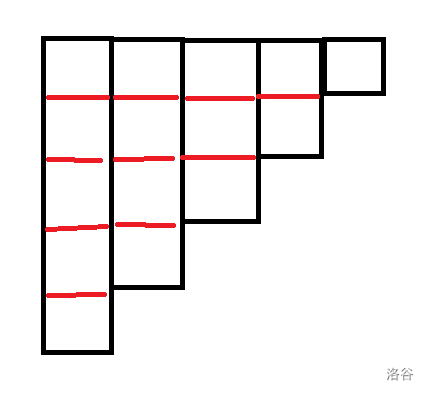
图中的 \(\frac{5 \times 4}{2}=10\) 条红色的线，表示在第一张图（未旋转的图）中，红线取左右两边的元素构成一个二元组。（第二张图就是上下两个元素）

旋转后图形的第一行有 \(4\) 条红线，就对应着 \(n-1\) 条差为 1 的二元组；第二行有 \(3\) 条红线，就对应着 \(n-2\) 条差为 2 的二元组……

也就是寻找一种构造方案，使得旋转过后的图中每一列的第一行红线相差 1，第二行相差 2，第 3 行相差 3……

那么有如下构造：

\[x,x+1,x-1,x+2,x-2,\cdots
\]

直接枚举每一个 \(x\) 直到 \(x\) 变换出来的数不在 \([1,n]\) 范围之内即可。

例如 \(n=7\) 时，枚举 \(x\) 得到的序列：

1 2
2 3 1 4
3 4 2 5 1 6
4 5 3 6 2 7 1
5 6 4 7 3
6 7 5
7

将序列长度排序，即为答案：

7
1 2
6 7 5
2 3 1 4
5 6 4 7 3
3 4 2 5 1 6
4 5 3 6 2 7 1

时间复杂度 \(O(n^2)\)。

CODE

#include<bits/stdc++.h>
using namespace std;

const int maxn=4005;

int n;
int a[maxn][maxn];

pair<int,int> p[maxn];

int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        int x=i,t=i,ct=0,bj=-1,xz=0;
        while(t<=n&&t>=1)
        {
            ct++;
            a[i][ct]=t;
            bj*=-1;
            xz+=ct%2;
            t=x+bj*xz;
        }
        p[i]=make_pair(ct,i);
    }
    sort(p+1,p+n+1);
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=i;j++) printf("%d ",a[p[i].second][j]);
        printf("\n");
    }
}

后记

樱雪喵 ORZ