解决 windows 10 WSL 安装Ubuntu后 屏幕亮度飙至最高 且屏幕亮度无法调节 外接显示器无法显示 的问题

转载请注明出处：博客园 博主Bubgit https://www.cnblogs.com/Bubgit/p/16367937.html

问题现象

自从windows 10推出了 wsl (Windows Subsystem for Linux ) 之后，再搭配上vscode的远程资源管理器（WSL target），简直不要太好用！

但是在Microsoft Store 里面搜索ubuntu 安装完成之后，不会有任何问题，直到重启之后，我的笔记本（华硕K501L）出现：屏幕亮度飙至最高，且无法调节屏幕亮度，外接显示屏没有画面（hdmi插入电脑都没发现设备），很明显显示驱动出现了问题。

刚开始我一直没有定位到问题在哪里，因为这个问题是安装完ubuntu，并且重启之后才会出现，当时恰逢windows更新推送了，我是windows更新提示重启，重启之后发现出了这个问题，当时以为是windows更新出现了问题，于是一顿折腾：更新最新的windows版本更新，重装显卡驱动，回退更新，最后没办法只能重装了系统，网上也找了n多资料，也没有和我一样的情况，后来尝试复现，折腾了好久，重装电脑好几次，最后定位到是wsl安装ubuntu之后，重启电脑就会导致这个问题，能够稳定复现，但是也没有比较好的方法解决，重装显卡驱动也没办法解决，只好用docker 启了一个linux 再用vscode containers连进去，使用linux开发环境。

直到昨天，终于解决了这个问题，特此记录，给大家提供解决思路。

解决方法

首先还是再windows Microsoft Store 里面搜索ubuntu安装，并且再windows power shell 以管理员身份运行 输入

wsl --set-default-version 2

设置wsl默认启动应用版本为wsl2，默认是1，（wsl1按照下面的步骤可能无法解决问题）

红框标注的两个版本，安装后多半会出现问题，建议选择安装第一个

安装完成之后，如果出现屏幕显示问题，这个时候按以下步骤操作

1、卸载已经安装的ubuntu，再重新安装这个版本的ubuntu

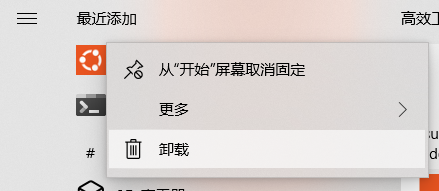
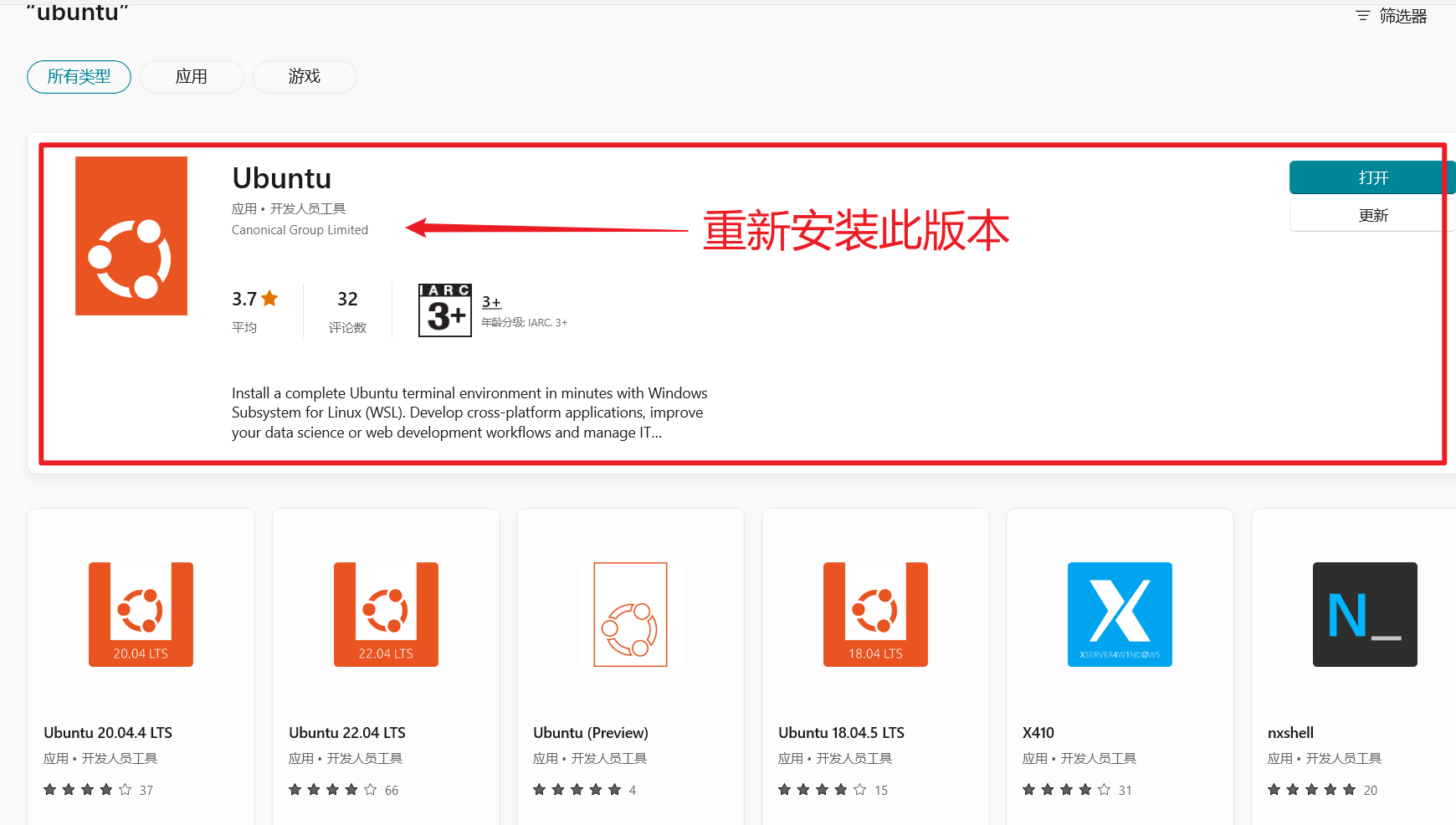
2、卸载windows显示驱动

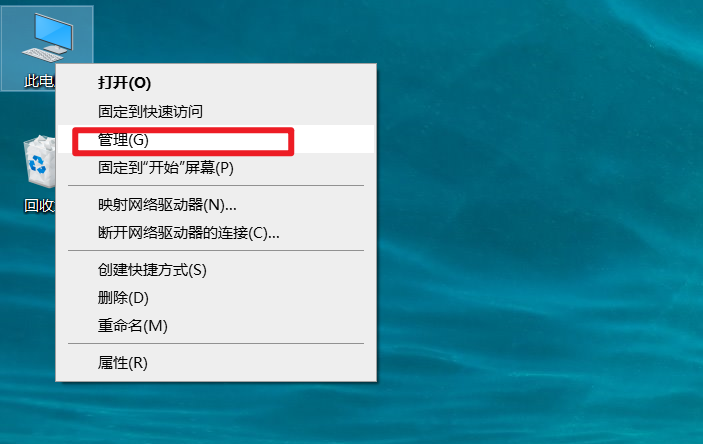
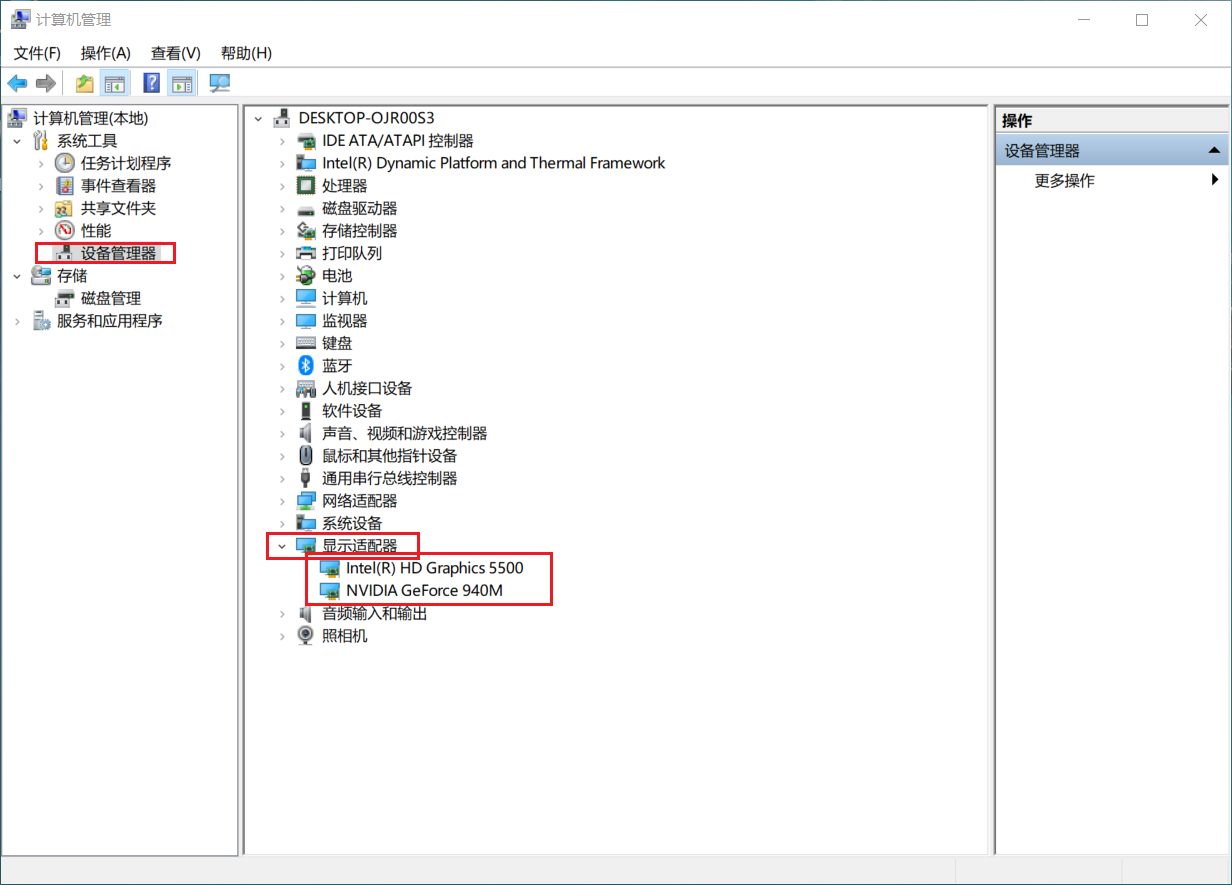
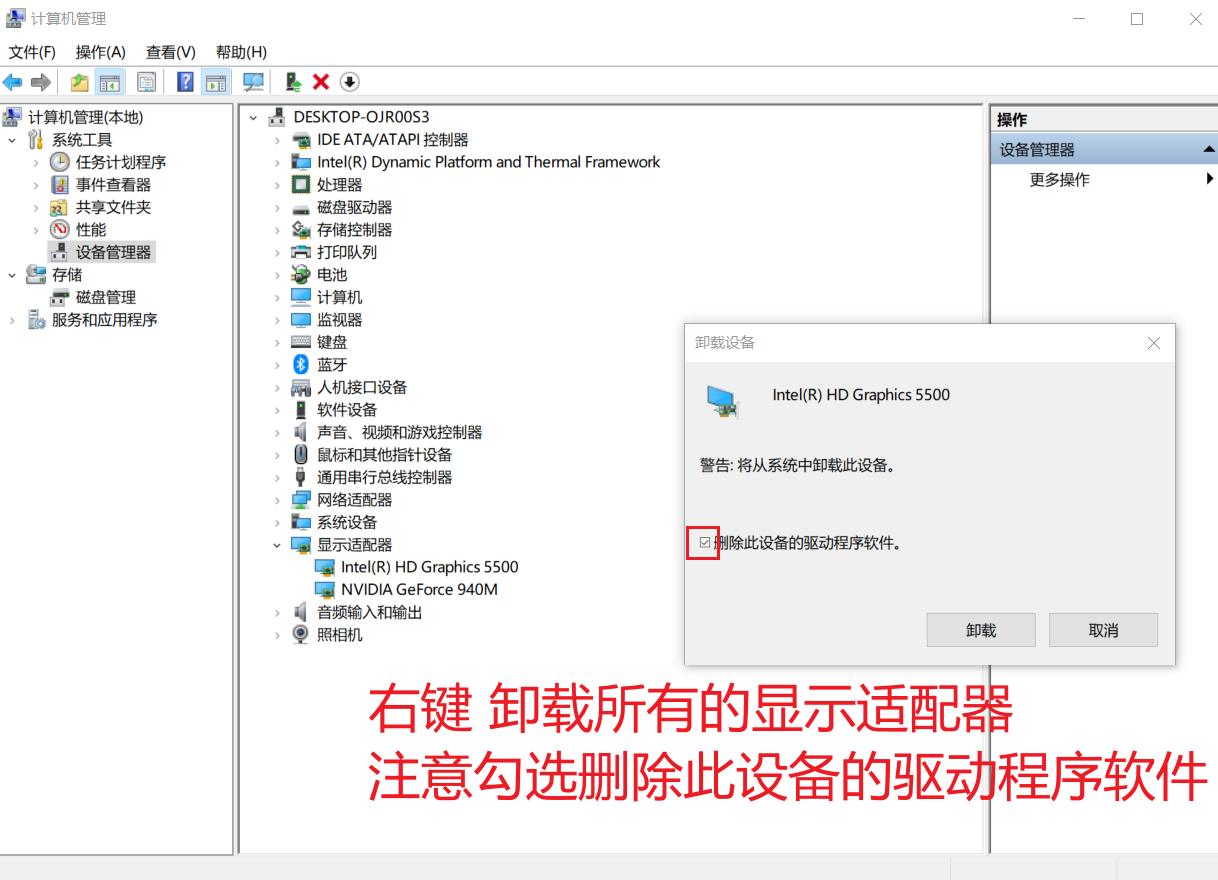
3、检查下有没有可更新的windows更新，有的话就立即更新，更新完了之后重启电脑，没有的话就直接重启电脑，重启电脑之后应该会发现显卡驱动是windows自带的基础显示驱动，这个时候屏幕应该已经不是最高亮度了（不过因为是基础显示驱动，亮度还是不可调）。

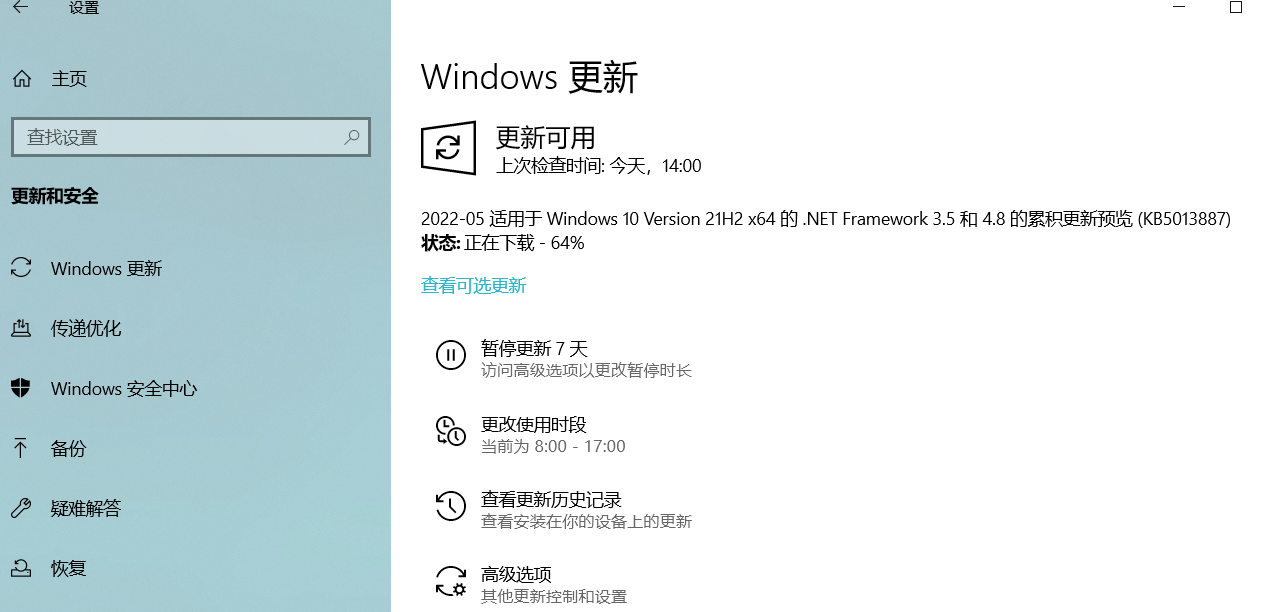
4、接下来久等着，没错，就是等着windows自动把我们已经卸载了的显卡驱动都帮我们装回来，开机等会儿，再检查下windows更新,保持是最新版的windows 10， 应该要不了多久，windows会自动联网把确实的显卡驱动安装回来。接着重启之后就会发现，显卡驱动正常了，亮度可调，外接屏幕显示正常，ubuntu也能正常工作，皆大欢喜，美滋滋。