Hetao P1178 冒险者 题解 [ 绿 ][ 最短路 ][ 线性 dp ]

冒险者

题解

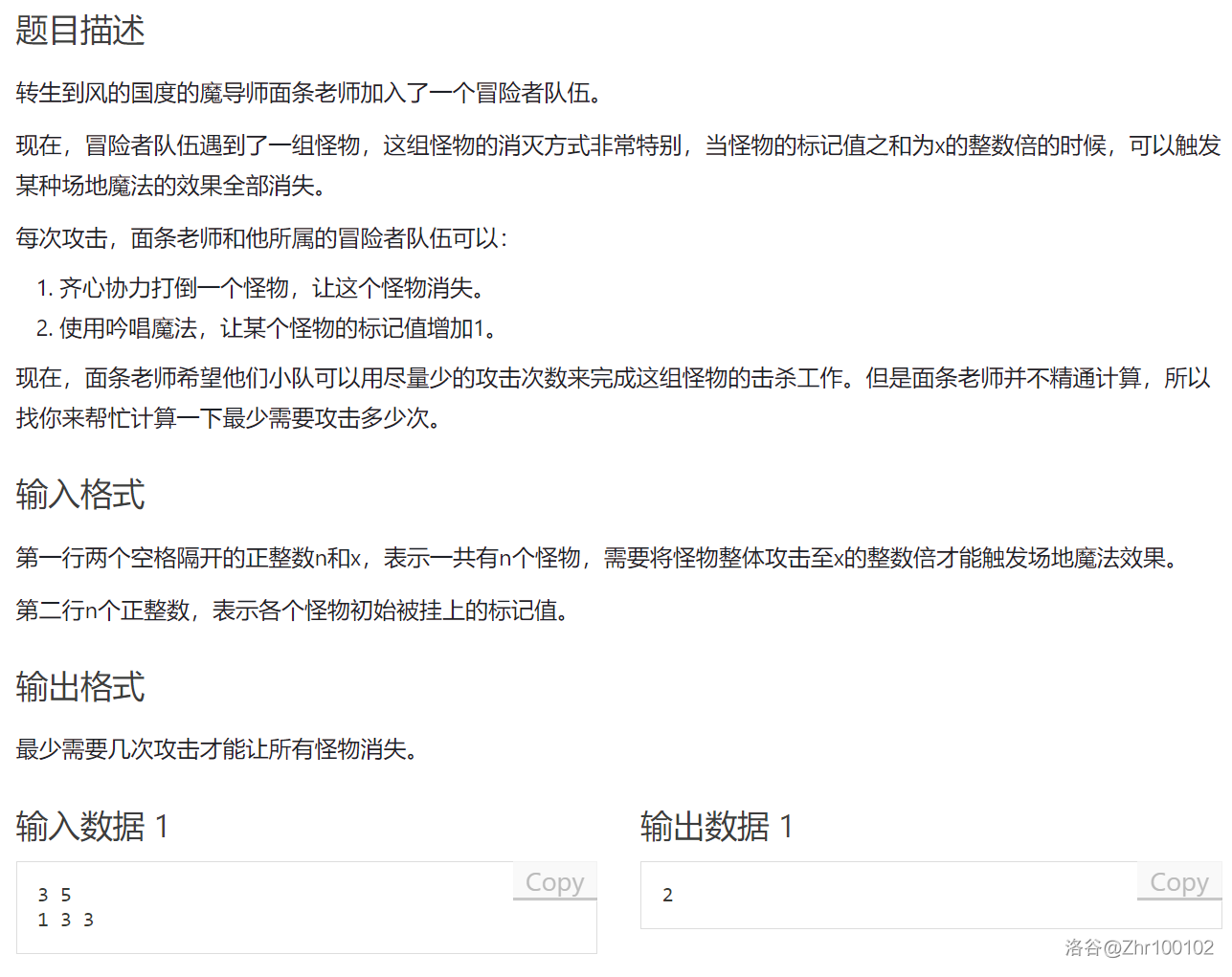
本蒟蒻采用的和大部分人解法不同，是根据当前标记值的总和跑最短路的一种解法。

思路 30min ,调代码 2h 的我太蒻了

首先观察题面可以发现本题求的是最少操作数，由于要求最小且有变化的过程，所以可以使用 dp 求解，也可以使用 最短路算法 求解，本篇先介绍最短路的算法。

其实作为图论来解还挺需要思维的。

最短路做法

建图

可以把本题抽象为以下的问题：

以编号为 \(\sum_{i = 1}^{n} a_i\) 的节点为起点，每次可以减去任何一个 \(a_i\) 并到达编号为这个数的节点，每个 \(a_i\) 最多可以减去一次；每次也可以加上一个 \(1\) 并到达编号为这个数的节点，有无限次数，任何边的权值都为 \(1\) ，求到达编号为 \(x\) 的倍数的节点的最短路。

实现

写题解的时候突然发现由于边权为 1 ，所以本题可以使用 bfs 用 \(O(n)\) 的时间进行求解，数据甚至可以更大一些。

但考试的时候没想那么多，就使用了 Dijkstra 算法，时间为 \(O(m \log m)\)，由于边数可能比较多，因此不提前建出边来，而是对每个节点临时建边。看似复杂度很大，实际上有效边数并没有这么多，最大的数据也只跑了 13ms ，若用 bfs 可能会更少。

同时注意到每个数只能被减去一次，由于堆优化 dijkstra 的堆中每个情况是相对独立的，所以每个情况都要开额外的一个数组来存储每个数是否使用过，为了节省空间防止 MLE ，这里采用 bitset 来压缩空间。就是这里写错下标导致我调了 2h。

然后其他的就按照正常的最短路跑就行了。

代码

直接贺了赛时的 dijkstra 上去，什么时候有时间再来写 bfs 版和 dp 版的吧。

#include <bits/stdc++.h>
using namespace std;
int n,x;
int a[1005],start=0;
int dis[1001005];
bool vis[1001005];
struct node{
	bitset<1005>bs;
	int f,s;
}tmp,tmp2;
struct cmp{
	bool operator()(node b,node c)
	{
		return c.f<b.f;
	}
};
int dijkstra()
{
	memset(dis,0x3f,sizeof(dis));
	priority_queue<node,vector<node>,cmp> q;
	tmp.f=0,tmp.s=start;
	q.push(tmp);
	dis[start]=0;
	while(!q.empty())
	{
		tmp=q.top();
		q.pop();
		int oridis=tmp.f,u=tmp.s;
		if(u%x==0)
		{
			return dis[u];
		}
		if(vis[u])continue;
		vis[u]=1;
		for(int i=1;i<=n;i++)
		{
			if(tmp.bs[i]==0)
			{
				int v=u-a[i];
				if(dis[v]>oridis+1)
				{
					dis[v]=oridis+1;
					tmp2.f=dis[v],tmp2.s=v;
					tmp2.bs=tmp.bs;
					tmp2.bs[i]=1;//就是这个下标坑我2h
					q.push(tmp2);
				}
			}
		}
		int v=u+1;
		if(v<=start+1000 && dis[v]>oridis+1)//最多操作次数为1000次
		{
			dis[v]=oridis+1;
			tmp2.f=dis[v],tmp2.s=v;
			tmp2.bs=tmp.bs;
			q.push(tmp2);
		}
	}
	return n;
}
int main()
{
	freopen("player.in","r",stdin);
	freopen("player.out","w",stdout);
	cin>>n>>x;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
		start+=a[i];
	}
	int res=dijkstra();
	cout<<res;
	return 0;
}

dp 做法

没有想到这个做法的原因主要还是最近 dp 有点生疏，一直往利用元素的条件来想，而忽视了靠元素的数值来解决问题。

这是典型的以数字设计 dp ，而不是用元素设计的一道题，从 \(a_i\le 1000\) 就可以看出。

同时，对于一个数删不删除，对应着 2 种状态，并且一旦知道删了哪些数，就可以推出这时要加多少个 1 。所以，就此设计转移方程式即可。

第一维是一个常见的 dp 设计思路：对于前 \(i\) 个数进行选择的结果，第二维是当前的数的总和 $sum \mod x $ 的结果。

于是，定义 \(f[i][j]\) 表示在前 \(i\) 个数中，使存在的数的总和 \(\mod x\) 为 \(j\) 时，最少删去的数的数量。

转移方程式为：\(f[i][j]=\min(f[i-1][j]+1,f[i-1][(j-a[i]+x)\mod x])\) ，其中 $ 1\le i\le n , 0\le j <x $。

最后计算答案时，直接输出 $\min(f[n][j]+(x-j)\mod x) , 0\le j <x $ 即可。

然后还要注意一点：初始化 \(f[0][0]=0\) 。

时间 \(O(nx)\) 。

未优化代码如下：

#include <bits/stdc++.h>
using namespace std;
int a[1005],n,f[1005][1005],x;
int main()
{
	freopen("player.in","r",stdin);
	freopen("player.out","w",stdout);
	memset(f,0x3f,sizeof(f));
	f[0][0]=0;
	cin>>n>>x;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
		a[i]%=x;
	}
	for(int i=1;i<=n;i++)
	{
		for(int j=0;j<x;j++)
		{
			f[i][j]=min(f[i-1][j]+1,f[i-1][(j-a[i]+x)%x]);
		}
	}
	int ans=0x3f3f3f3f;
	for(int i=0;i<x;i++)
	{
		ans=min(ans,f[n][i]+(x-i)%x);
	}
	cout<<ans;
	return 0;
}

优化

注意到动态转移方程式的第一维只会用到 \(i-1\) 的值，所以可以强行进行滚动数组优化，虽然不这样做也可以过就是了。

滚动数组优化代码：

#include <bits/stdc++.h>
using namespace std;
int a[1005],n,f[2][1005],x;
int main()
{
	freopen("player.in","r",stdin);
	freopen("player.out","w",stdout);
	memset(f,0x3f,sizeof(f));
	f[0][0]=0;
	cin>>n>>x;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
		a[i]%=x;
	}
	for(int i=1;i<=n;i++)
	{
		for(int j=0;j<x;j++)
		{
			f[i&1][j]=min(f[(i&1)^1][j]+1,f[(i&1)^1][(j-a[i]+x)%x]);//i&1=i%2,(i&1)^1=(i+1)%2
		}
	}
	int ans=0x3f3f3f3f;
	for(int i=0;i<x;i++)
	{
		ans=min(ans,f[n&1][i]+(x-i)%x);
	}
	cout<<ans;
	return 0;
}