用python做时间序列预测六：相关函数图、偏相关函数图、滞后图

经典的时间序列预测方法都是假设如果一个时间序列有显著的自相关性，那么历史值对预测当前值会很有帮助，但是究竟取多少阶的历史值，就需要通过分析相关函数图和偏相关函数图来得到。本文介绍如何什么是相关函数图和偏相关函数图，另外还会介绍一下滞后图。

什么是自相关和偏自相关函数？

• 先来解释下滞后阶数n，如果当前值和前2期的值有关，则n=2，那么可以用时间序列和它的2阶滞后序列来训练一个自回归模型，预测未来的值。
• 自相关函数(ACF)表达了时间序列和n阶滞后序列之间的相关性(考虑了中间时刻的值的影响，比如t-3对t的影响中，就同时考虑了t-2，t-1对t的影响)。
• 偏自相关函数(PACF)表达了时间序列和n阶滞后序列之间的纯相关性(不考虑中间时刻的值的影响，比如t-3对t的影响中，不会考虑t-2，t-1对t的影响)。如果用自回归方程来预测t时刻的值，则各滞后阶数的系数就是各滞后阶数下的偏自相关值，比如下面方程的α1，α2，α3，分别是1阶滞后，2阶滞后，3阶滞后下的偏自相关值。
  
  

ACF 和 PACF 可视化

from statsmodels.tsa.stattools import acf, pacf
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf

df = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv')
# Calculate ACF and PACF upto 50 lags# acf_50 = acf(df.value, nlags=50)# pacf_50 = pacf(df.value, nlags=50)
# Draw Plot
fig, axes = plt.subplots(1,2,figsize=(16,3), dpi= 100)
plot_acf(df.value.tolist(), lags=50, ax=axes[0])
plot_pacf(df.value.tolist(), lags=50, ax=axes[1])

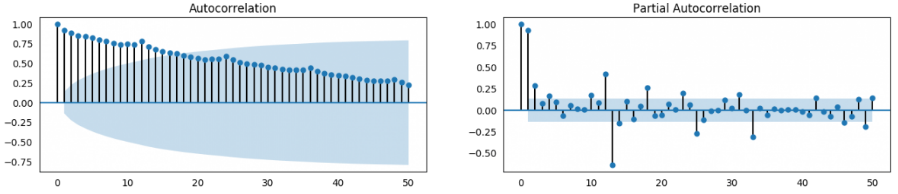
• 如果ACF表现为长拖尾(如上左图)，说明带有趋势，需要做差分。
• 如果ACF的1阶滞后就截尾，则可能是过度差分了(差分会降低相关性)。
• 如果ACF拖尾一点点，然后截尾的情况下，选择的差分阶数是比较合适的。此时可以用前n个历史时刻的值做自回归来预测当前值，关于n的取值则可以参考PACF的截尾处，假设上右图是差分后的pacf图，在第2个滞后阶数后(从第0开始，0阶滞后下就是原序列和原序列相比，相关性为1)就骤然降到了相关性置信区间内,则表示95%的概率不具有相关性，所以该序列可以做2阶滞后自回归。

什么是相关性置信区间？

对于白噪声序列，按理说不会有任何自相关性，我们期望的自相关性为0，但是由于随机扰动的存在，自相关性不会为0，而通常假设随机扰动符合标准正态分布(均值为0，标准差为1)，那么这个随机扰动的95%置信区间(一般都取95%,当然也可以调整这个概率)可以通过如下算式计算



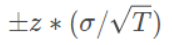
标准正态分布的z分数表示距离均值有几个标准差，σ除以根号T表示有偏样本标准差，

这里95%置信度下z分数=1.96，标准差σ=1，T是序列长度，则置信区间计算如下：



表示对于白噪声序列，95%的自相关性落在这个置信区间内。

而这个置信区间就是上面acf和pacf图中的相关性区间了，也就是说如果滞后阶数与原序列的相关性落在这个区间内，就表示不相关。

滞后图

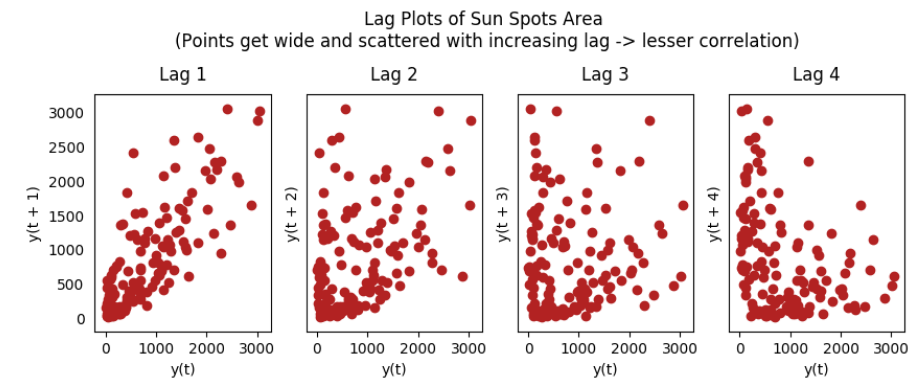
滞后图是用时间序列和相应的滞后阶数序列做出的散点图。可以用于观测自相关性。

from pandas.plotting import lag_plot
plt.rcParams.update({'ytick.left' : False, 'axes.titlepad':10})

# Import
ss = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/sunspotarea.csv')
a10 = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv')

# Plot
fig, axes = plt.subplots(1, 4, figsize=(10,3), sharex=True, sharey=True, dpi=100)for i, ax in enumerate(axes.flatten()[:4]):
    lag_plot(ss, lag=i+1, ax=ax, c='firebrick')
    ax.set_title('Lag ' + str(i+1))

fig.suptitle('Lag Plots of Sun Spots Area \n(Points get wide and scattered with increasing lag -> lesser correlation)\n', y=1.15)    

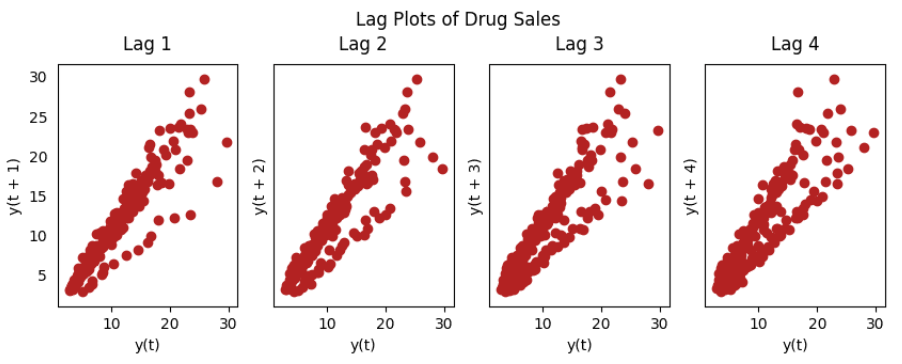
fig, axes = plt.subplots(1, 4, figsize=(10,3), sharex=True, sharey=True, dpi=100)for i, ax in enumerate(axes.flatten()[:4]):
    lag_plot(a10, lag=i+1, ax=ax, c='firebrick')
    ax.set_title('Lag ' + str(i+1))

fig.suptitle('Lag Plots of Drug Sales', y=1.05)
plt.show()

ok,本篇就这么多内容啦~，感谢阅读O(∩_∩)O。