[算法]树上倍增求LCA

　　LCA指的是最近公共祖先(Least Common Ancestors)，如下图所示:

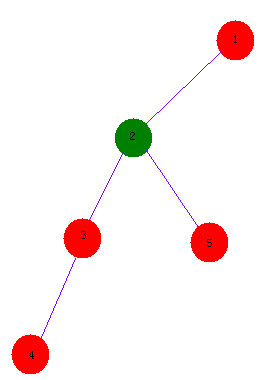
　　4和5的LCA就是2

　　那怎么求呢？最粗暴的方法就是先dfs一次，处理出每个点的深度

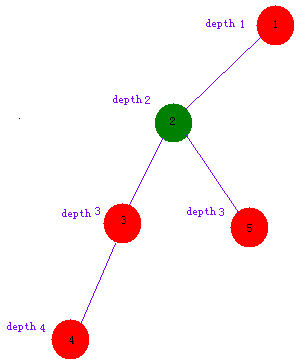
　　然后把深度更深的那一个点（4）一个点地一个点地往上跳，直到到某个点（3）和另外那个点（5）的深度一样

然后两个点一起一个点地一个点地往上跳，直到到某个点（就是最近公共祖先）两个点“变”成了一个点

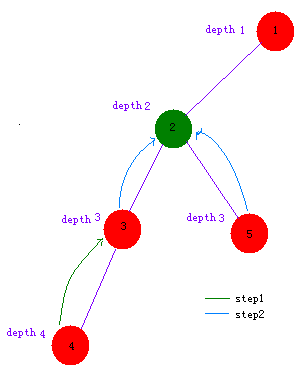
　　不过有没有发现一个点地一个点地跳很浪费时间？

如果一下子跳到目标点内存又可能不支持，相对来说倍增的性价比算是很高的

　　倍增的话就是一次跳2ⁱ 个点，不难发现深度差为x时，深度更深的那个点就需要跳x个点

于是可以写出这段代码

 if(depth[a] < depth[b])    swap(a, b);
 int c = depth[a] - depth[b];
 for(int i = ; i <= ; i++){
     if(c & ( << i)){
         a = up[a][i];
     }
 }

　　接下来很快就会发现一个很严重的问题:两个点按照这样跳，不能保证一定是最近的

所以倍增找lca的方法是这样的:

　　从最大可以跳的步数开始跳(一定是2ⁱ)，如果跳的到的位置一样，就不跳，如果不一样才跳，每次跳的路程是前一次的一半

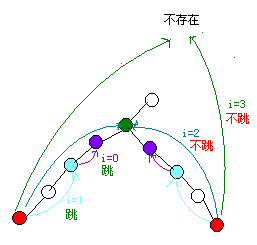
　　过程大概就像上图所示，但是执行完了这一段到的点不是最近公共祖先，但是，它们再往上跳一格，就到了

把这一段写成代码，就成了这样：

 for(int i = ; i >= ; i--){
     if(up[a][i] != up[b][i]){
         a = up[a][i];
         b = up[b][i];
     }
 }

　　前面还需要加上一句特判（当a和b在同一边时，深度浅的那个点就是最近公共祖先）

if(a == b)    return a;

　　好了，会求lca了，关键是怎么构造倍增数组。

没有疑问的是向上跳一格就是自己的父节点

f[i][] = fa[i];

　　这个是初值，接着可以根据这个推出来其他的，除此之外还要附上初值0，不然有可能会RE

f[i][j] = f[f[i][j - ]][j - ];

　　就是把这一段路，分成两段已经知道的

　　完整代码就是这样的:

 Matrix<int> up;
 inline void init_bz(){
     up = Matrix<int>(, n + );
     memset(up.p, , sizeof(int) *  * (n + ));
     for(int i = ; i <= n; i++){
         up[i][] = fa[i];
     }
     for(int j = ; j <= ; j++){
         for(int i = ; i <= n; i++){
             up[i][j] = up[up[i][j - ]][j - ];
         }
     }
 }

　　注意倍增求LCA适用于询问多的情况，不然光在预处理上花的时间就已经够多了（如果只有一两个询问，直接暴力就好了）

　　当然，这个倍增算法判断条件是若干级祖先是否相等。

　　同样，点$u$，$v$的LCA还满足它是其中一个点的最近的一个祖先，满足$u$，$v$都在它的子树中。

　　判断一个点是否在另一个点的子树中，我们可以用dfs序来判断。

　　这是倍增的另一种判断方法：

 1 void dfs(int p, int fa) {
 2     bz[p][0] = fa, in[p] = ++cnt;
 3     for (int i = 1; i < bzmax; i++)
 4         bz[p][i] = bz[bz[p][i - 1]][i - 1];
 5     for (int i = g.h[p]; ~i; i = g[i].nx) {
 6         int e = g[i].ed;
 7         if (e == fa)    continue;
 8         dfs(e, p);
 9     }
10     out[p] = cnt;
11 }
12
13 int lca(int a, int b) {
14     if (dep[a] > dep[b])    swap(a, b);
15     if (in[a] <= in[b] && out[a] >= out[b])
16         return a;
17     for (int i = bzmax - 1, nx; ~i; i--) {
18         nx = bz[a][i];
19         if (!(in[nx] <= in[b] && out[nx] >= out[b]))
20             a = nx;
21     }
22     return bz[a][0];
23 }
24