POJ 1182 食物链 （三态种类并查集）

这题首先不说怎么做，首先要提醒的是。。：一定不要做成多组输入，，我WA了一个晚上加上午，，反正我是尝到苦头了，，请诸君千万莫走这条弯路。。切记

这题是上一题（Find them and Catch them）的难度更高的版本，如果你没做的话建议先做那个，用并查集来解，分成三种状态，因为要查询关系，直接查无法查，于是以根节点作为中继点，每个节点做一个标记表示与根节点的关系，0表示与根同类，1表示吃根，2表示被根吃，也必须是这三个数，不能使-1,1，0或别的什么的，因为那样无法转化。

在findset时要记得根据该节点与其父节点的关系和父节点与爷爷节点的关系来推出该节点与他的爷爷节点的关系，做到实时更新（因为合并会使他的标记变化）。

然后合并： 标记： ca[x];

在findset时要记得根据该节点与其父节点的关系和父节点与爷爷节点的关系来推出该节点与他的爷爷节点的关系，做到实时更新（因为合并会使他的标记变化）。

然后合并：
标记： ca[x];

.如果断言为a和b同类
{
    .如果在同一集合，判断ca[a]是否等于ca[b]
    .不在同一集合则合并，此时
        ca[x] = (-ca[a] + ca[b] + )%;   //加3是为了防止负数
        因为图示：
}
.如果断言为a吃b
{
    .如果在一个集合，判断是否有a吃b的关系
        if((ca[a] + )% =?= ca[b])..
            怎么来的自己可以推导一下
    .如果不在，合并
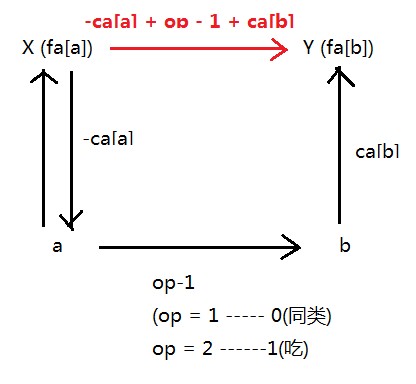
        ca[x] = (-ca[a] +  + ca[b] + )%;  //加3是为了防止负数
}

图示：

下面上代码：

#include <iostream>
#include <cstdio>
using namespace std;
#define N 50100
int fa[N],ca[N];

void makeset(int n)
{
    for(int i=;i<=n;i++)
    {
        fa[i] = i;
        ca[i] = ;   // 0:同类  1:吃  2:被吃
    }
}

int findset(int x)
{
    if(x != fa[x])
    {
        int tmp = fa[x];
        fa[x] = findset(fa[x]);
        ca[x] = (ca[x] + ca[tmp])%;
    }
    return fa[x];
}

int unionset(int op,int a,int b)
{
    int x = findset(a);
    int y = findset(b);
    if(op == )  //a与b是同类关系
    {
        if(x == y)  //如果已经在一个集合里面了，则判断这句话的真假即可
        {
            if(ca[a] == ca[b])
            {
                return ;   //假话增量为0，说明是真话
            }
            else
                return ;   //假话增量为1，说明是假话
        }
        else   //还不在一个集合中，合并两个集合
        {
            fa[x] = y;
            ca[x] = (-ca[a] + ca[b] + )%;
        }
    }
    else     //op = 2 ,a吃b的关系
    {
        if(x == y)   //在一个集合中，判断是否正确
        {
            if((ca[a] + )% == ca[b])  //这样才能形成 a吃b吃gen吃a 即形成a 吃 b 的关系
            {
                return ;  //假话增量为0
            }
            else
                return ;
        }
        else    //不在一个集合中，合并
        {
            fa[x] = y;
            ca[x] = (-ca[a] +  + ca[b])%;
        }
    }
    return ;   //不处理的返回值
}

int main()
{
    int n,k,cnt,i;
    int op,a,b;
    scanf("%d%d",&n,&k);
        cnt = ;
        makeset(n);
        for(i=;i<k;i++)
        {
            scanf("%d%d%d",&op,&a,&b);
            if(a > n || b > n)
                cnt++;
            else if(op ==  && a == b)
                cnt++;
            else
                cnt += unionset(op,a,b);
        }
        cout<<cnt<<endl;
    return ;
}

还可以参考：

http://blog.csdn.net/shuangde800/article/details/7974668

http://blog.csdn.net/freezhanacmore/article/details/8767413