[线性代数] 线性子空间入門 Basic Vector Subspaces

导语：其他集数可在[线性代数]标籤文章找到。线性子空间是一个大课题，这里先提供一个简单的入门，承接先前关于矩阵代数的讨论，期待与你的交流。

Overview: Subspace definition

In a vector space of Rⁿ, sets of vectors spanning a volume EQUAL TO OR SMALLER THAN that of Rⁿ form subspaces of that vector space of Rⁿ. A subset H of Rⁿ is defined as follow:

1. Zero vector included in H
2. Subspace spanned by H closed under addition and scalar multiplication

Sketch of proof of property(1): H=Span{v1, v2, v3}, if weights to every columns in H equals to 0, we get a zero vector. If, for all possible linear combinations of H, zero vector is not involved, span of H is not a subspace of Rⁿ. It must belong to another vector space R^x, whose zero vector is included by the span of H. If, for the following, let Q={u,v} be a subspace of Rⁿ and L={z} be a subspace of R^x. L does not contain zero vector in Rⁿ thus not a subspace of Rⁿ.

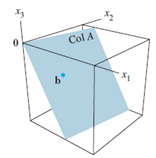
Column space, Null space

Column space of a matrix A, i.e. Col A, refers to span of columns in A, i.e. all the possible linear combinations of pivot columns in A. (Recall non-pivot columns are simply linear combinations of other pivot columns, so they do not matter in spanning.) Alternatively, it refers to all the possible b where Ax=b is consistent, as illustrated follows:

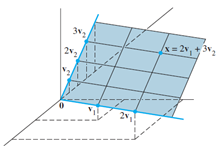
Nul A, on another hand, refers to the spanning from all possible solutions for Ax=0. Recall when x=0, it is the trivial solution to homogeneous equation. Thus, automatically satisfy requirement (1) in the definition of subspace. The dimension of non-trivial solution must equal to number of columns in A, so the resultant vector would also be 0, satisfying the right-hand side of the equation. For instance, if A is an mxn matrix, Nul(A) must be a subspace for Rⁿ.

Both Col(A) and Nul(A) are subspaces which contain infinitely many vectors in a set, most of them are just the linear combination of few key vectors, the basis vectors. Basis vectors are the most simplified set of linearly independent vectors representing a subspace, as the linear combination of all vectors inside regenerate the subspace. A standard basis is shown below:

There exists some interesting relationship between finding the BASIS for null space and column space for the same matrix A. Take the following matrices as examples. To find Nul(A), simply row reduce it into row echelon form and solve for x, which should automatically generate a set of linearly independent vectors from the FREE variables. To find Col(A), we just need to find the linearly independent vectors in matrix A. In words, whenever an elementary row operation is applied on A, we get a new echelon form. Each of them has its own basis set for their column space. It has great implication, as we know row operations generate new column space from its set of linearly independent columns in the matrix.

Dimension and rank

Dimension refers to the number of vectors in Nul(A) or Col(A), but rank only refers to that in Col(A). Weights assigned to each linearly independent vector within the basis are called coordinates, which is an ordered set of weights to vectors within basis. Given vectors in basis linearly independent, there's only one way for them to generate each 'point' within the corresponding subspace they span. Thus, dimensionality simply refers to number of coordinates/weights to a vector set, thus also refers to the number of vectors within the set. Noted that dimension need not equal to the dimension of Rⁿ. For example, the following shows a two-dimensional subspace of R³, where the subspace only has a dimension of 2. Recalled that since the dimension here is 2, where 2!=3, thus, the basis vector of this set do not span R³. The spanning of vectors in subspace can become a subspace of R³ as each of them is also a three-dimensional vector.

As we have witnessed that Nul(A) comes from free variables while Col(A) comes from basic variables, the number of columns in a matrix A is inferred as follow:

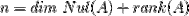
To form a basis for a p-dimensional subspace is simple. Simply pick any p linearly independent vectors from the space will give you a basis for the subspace

Invertibility

All discussion above can be generalized into the invertible matrix theorem covered in earlier posts. Suppose A is an nxn matrix, all of the followings implies A is invertible.

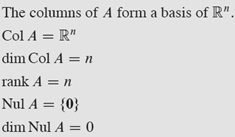
Above basically states that, for a nxn matrix, if it spans Rⁿ, then it must be invertible. And the rules above suggest how to determine if a nxn matrix contains no linearly dependent columns from their rank and dimension. Nothing new.

Examples

(More to come…stay tuned…)