小书匠Graph图论

重头戏部分来了,写到这里我感觉得仔细认真点了,可能在NetworkX中,实现某些算法就一句话的事,但是这个算法是做什么的,用在什么地方,原理是怎么样的,不清除,所以,我决定先把图论中常用算法弄个明白在写这部分.

图论常用算法看我的博客:

下面我将使用NetworkX实现上面的算法,建议不清楚的部分打开两篇博客对照理解.

我将图论的经典问题及常用算法的总结写在下面两篇博客中:

图论---问题篇

图论---算法篇

目录:

注意:如果代码出现找不库,请返回第一个教程,把库文件导入.

11.Graph相关算法

11.1最短路径

11.1.1无向图和有向图

  1. #定义并画出该图 
  2. G = nx.path_graph(5) 
  3. nx.add_path(G,[0,5,2]) 
  4. nx.add_path(G,[0,6,4]) 
  5. nx.draw(G,with_labels=True) 
  6. plt.title('无向图',fontproperties=myfont) 
  7. plt.axis('on') 
  8. plt.xticks([]) 
  9. plt.yticks([]) 
  10. plt.show() 
  12. #计算最短路径 
  13. print('0节点到4节点最短路径: ',nx.shortest_path(G, source=0, target=4)) 
  14. p1 = nx.shortest_path(G, source=0) 
  15. print('0节点到所有节点最短路径: ',p1) 
  17. #计算图中所有的最短路径 
  18. print('计算图中节点0到节点2的所有最短路径: ',[p for p in nx.all_shortest_paths(G, source=0, target=2)]) 
  20. #计算最短路径长度 
  21. p2=nx.shortest_path_length(G, source=0, target=2) #最短路径长度 
  22. p3=nx.average_shortest_path_length(G) #计算平均最短路径长度 
  23. print('节点0到节点2的最短路径长度:',p2,' 平均最短路径长度: ',p3) 
  25. #检测是否有路径 
  26. print('检测节点0到节点2是否有路径',nx.has_path(G,0,2)) 

无向图和有向图最短路径示例

输出:

  1. 0节点到4节点最短路径: [0, 6, 4] 
  2. 0节点到所有节点最短路径: {0: [0], 1: [0, 1], 2: [0, 1, 2], 3: [0, 1, 2, 3], 4: [0, 6, 4], 5: [0, 5], 6: [0, 6]} 
  3. 计算图中节点0到节点2的所有最短路径: [[0, 1, 2], [0, 5, 2]] 
  4. 节点0到节点2的最短路径长度: 2 平均最短路径长度: 1.8095238095238095 
  5. 检测节点0到节点2是否有路径 True 

11.1.2无权图

  1. G = nx.path_graph(3) 
  2. nx.draw(G,with_labels=True) 
  3. plt.title('无权图',fontproperties=myfont) 
  4. plt.axis('on') 
  5. plt.xticks([]) 
  6. plt.yticks([]) 
  7. plt.show() 
  9. path1 = nx.single_source_shortest_path(G, 0) #计算当前源与所有可达节点的最短路径 
  10. length1 = nx.single_source_shortest_path_length(G, 0) #计算当前源与所有可达节点的最短路径的长度 
  11. path2 = dict(nx.all_pairs_shortest_path(G)) #计算graph两两节点之间的最短路径 
  12. length2 = dict(nx.all_pairs_shortest_path_length(G)) #计算graph两两节点之间的最短路径的长度 
  13. prede1=nx.predecessor(G, 0) #返回G中从源到所有节点最短路径的前驱 
  15. print('当前源与所有可达节点的最短路径: ',path1,'\n当前源与所有可达节点的最短路径的长度: ',length1) 
  16. print('\ngraph两两节点之间的最短路径: ',path2,'\ngraph两两节点之间的最短路径的长度: ',length2) 
  17. print('\nG中从源到所有节点最短路径的前驱: ',prede1) 

无权图

输出:

  1. 当前源与所有可达节点的最短路径: {0: [0], 1: [0, 1], 2: [0, 1, 2]}  
  2. 当前源与所有可达节点的最短路径的长度: {0: 0, 1: 1, 2: 2} 
  3. graph两两节点之间的最短路径: {0: {0: [0], 1: [0, 1], 2: [0, 1, 2]}, 1: {0: [1, 0], 1: [1], 2: [1, 2]}, 2: {0: [2, 1, 0], 1: [2, 1], 2: [2]}}  
  4. graph两两节点之间的最短路径的长度: {0: {0: 0, 1: 1, 2: 2}, 1: {0: 1, 1: 0, 2: 1}, 2: {0: 2, 1: 1, 2: 0}} 
  5. G中从源到所有节点最短路径的前驱: {0: [], 1: [0], 2: [1]} 

11.1.3有权图(迪杰斯特拉)

  1. G = nx.path_graph(5, create_using = nx.DiGraph())  
  2. nx.draw(G,with_labels=True) 
  3. plt.title('有向图',fontproperties=myfont) 
  4. plt.axis('on') 
  5. plt.xticks([]) 
  6. plt.yticks([]) 
  7. plt.show() 
  9. #计算加权图最短路径长度和前驱 
  10. pred, dist = nx.dijkstra_predecessor_and_distance(G, 0) 
  11. print('\n加权图最短路径长度和前驱: ',pred, dist) 
  13. #返回G中从源到目标的最短加权路径,要求边权重必须为数值 
  14. print('\nG中从源0到目标4的最短加权路径: ',nx.dijkstra_path(G,0,4)) 
  15. print('\nG中从源0到目标4的最短加权路径的长度: ',nx.dijkstra_path_length(G,0,4)) #最短路径长度 
  17. #单源节点最短加权路径和长度。 
  18. length1, path1 = nx.single_source_dijkstra(G, 0) 
  19. print('\n单源节点最短加权路径和长度: ',length1, path1) 
  20. #下面两条和是前面的分解 
  21. # path2=nx.single_source_dijkstra_path(G,0) 
  22. # length2 = nx.single_source_dijkstra_path_length(G, 0) 
  23. #print(length1,'$', path1,'$',length2,'$',path2) 
  25. #多源节点最短加权路径和长度。 
  26. path1 = nx.multi_source_dijkstra_path(G, {0, 4}) 
  27. length1 = nx.multi_source_dijkstra_path_length(G, {0, 4}) 
  29. print('\n多源节点最短加权路径和长度:', path1,length1) 
  31. #两两节点之间最短加权路径和长度。 
  32. path1 = dict(nx.all_pairs_dijkstra_path(G)) 
  33. length1 = dict(nx.all_pairs_dijkstra_path_length(G)) 
  34. print('\n两两节点之间最短加权路径和长度: ',path1,length1) 
  36. #双向搜索的迪杰斯特拉 
  37. length, path = nx.bidirectional_dijkstra(G, 0, 4) 
  38. print('\n双向搜索的迪杰斯特拉:',length, path) 

迪杰斯特拉算法使用

输出:

  1. 加权图最短路径长度和前驱: {0: [], 1: [0], 2: [1], 3: [2], 4: [3]} {0: 0, 1: 1, 2: 2, 3: 3, 4: 4} 
  2. G中从源0到目标4的最短加权路径: [0, 1, 2, 3, 4] 
  3. G中从源0到目标4的最短加权路径的长度: 4 
  4. 单源节点最短加权路径和长度: {0: 0, 1: 1, 2: 2, 3: 3, 4: 4} {0: [0], 1: [0, 1], 2: [0, 1, 2], 3: [0, 1, 2, 3], 4: [0, 1, 2, 3, 4]} 
  5. 多源节点最短加权路径和长度: {0: [0], 1: [0, 1], 2: [0, 1, 2], 3: [0, 1, 2, 3], 4: [4]} {0: 0, 1: 1, 2: 2, 3: 3, 4: 0} 
  6. 两两节点之间最短加权路径和长度: {0: {0: [0], 1: [0, 1], 2: [0, 1, 2], 3: [0, 1, 2, 3], 4: [0, 1, 2, 3, 4]}, 1: {1: [1], 2: [1, 2], 3: [1, 2, 3], 4: [1, 2, 3, 4]}, 2: {2: [2], 3: [2, 3], 4: [2, 3, 4]}, 3: {3: [3], 4: [3, 4]}, 4: {4: [4]}} {0: {0: 0, 1: 1, 2: 2, 3: 3, 4: 4}, 1: {1: 0, 2:1, 3: 2, 4: 3}, 2: {2: 0, 3: 1, 4: 2}, 3: {3: 0, 4: 1}, 4: {4: 0}} 
  7. 双向搜索的迪杰斯特拉: 4 [0, 1, 2, 3, 4] 

11.1.4贝尔曼-福特(Bellman-Ford)算法

  1. G = nx.path_graph(5, create_using = nx.DiGraph())  
  2. nx.draw(G,with_labels=True) 
  3. plt.title('有权图',fontproperties=myfont) 
  4. plt.axis('on') 
  5. plt.xticks([]) 
  6. plt.yticks([]) 
  7. plt.show() 
  9. print('G中从源到目标的最短加权路径: ',nx.bellman_ford_path(G, 0, 4)) 
  10. print('\nG中从源到目标的最短加权路径的长度:',nx.bellman_ford_path_length(G,0,4)) 
  12. path1=nx.single_source_bellman_ford_path(G,0) 
  13. length1 = dict(nx.single_source_bellman_ford_path_length(G, 0)) 
  14. print('\n单源节点最短加权路径和长度: ',path1,'\n单源节点最短加权路径和长度: ',length1) 
  16. path2 = dict(nx.all_pairs_bellman_ford_path(G)) 
  17. length2 = dict(nx.all_pairs_bellman_ford_path_length(G)) 
  18. print('\n两两节点之间最短加权路径和长度: ',path2,length2) 
  20. length, path = nx.single_source_bellman_ford(G, 0) 
  21. pred, dist = nx.bellman_ford_predecessor_and_distance(G, 0) 
  22. print('\n加权图最短路径长度和前驱: ',pred,dist) 

贝尔曼-福特(Bellman-Ford)算法使用示例

输出:

  1. G中从源到目标的最短加权路径: [0, 1, 2, 3, 4] 
  2. G中从源到目标的最短加权路径的长度: 4 
  3. 单源节点最短加权路径和长度: {0: [0], 1: [0, 1], 2: [0, 1, 2], 3: [0, 1, 2, 3], 4: [0, 1, 2, 3, 4]}  
  4. 单源节点最短加权路径和长度: {0: 0, 1: 1, 2: 2, 3: 3, 4: 4} 
  5. 两两节点之间最短加权路径和长度: {0: {0: [0], 1: [0, 1], 2: [0, 1, 2], 3: [0, 1, 2, 3], 4: [0, 1, 2, 3, 4]}, 1: {1: [1], 2: [1, 2], 3: [1, 2, 3], 4: 

[1, 2, 3, 4]}, 2: {2: [2], 3: [2, 3], 4: [2, 3, 4]}, 3: {3: [3], 4:

[3, 4]}, 4: {4: [4]}} {0: {0: 0, 1: 1, 2: 2, 3: 3, 4: 4}, 1: {1: 0, 2:

1, 3: 2, 4: 3}, 2: {2: 0, 3: 1, 4: 2}, 3: {3: 0, 4: 1}, 4: {4: 0}}

加权图最短路径长度和前驱: {0: [None], 1: [0], 2: [1], 3: [2], 4: [3]} {0: 0, 1: 1, 2: 2, 3: 3, 4: 4}

11.1.5检测负权重边

  1. #定义并画出该图 
  2. G = nx.cycle_graph(5, create_using = nx.DiGraph()) 
  4. #添加负权重边前后 
  5. print(nx.negative_edge_cycle(G)) 
  6. G[1][2]['weight'] = -7 
  7. print(nx.negative_edge_cycle(G)) 

输出:

  1. False 
  2. True 

11.1.6使用约翰逊(Johnson)的算法

  1. #生成graph 
  2. G = nx.DiGraph() 
  3. G.add_weighted_edges_from([('0', '3', 3), ('0', '1', -5),('0', '2', 2), ('1', '2', 4), ('2', '3', 1)]) 
  5. #边和节点信息 
  6. edge_labels = nx.get_edge_attributes(G,'weight')  
  7. labels={'0':'0','1':'1','2':'2','3':'3'} 
  9. #生成节点位置  
  10. pos=nx.spring_layout(G)  
  12. #把节点画出来  
  13. nx.draw_networkx_nodes(G,pos,node_color='g',node_size=500,alpha=0.8)  
  15. #把边画出来  
  16. nx.draw_networkx_edges(G,pos,width=1.0,alpha=0.5,edge_color='b')  
  18. #把节点的标签画出来  
  19. nx.draw_networkx_labels(G,pos,labels,font_size=16)  
  21. #把边权重画出来  
  22. nx.draw_networkx_edge_labels(G, pos, edge_labels)  
  24. #显示graph 
  25. plt.title('有权图',fontproperties=myfont) 
  26. plt.axis('on') 
  27. plt.xticks([]) 
  28. plt.yticks([]) 
  29. plt.show() 
  31. #使用johnson算法计算最短路径 
  32. paths = nx.johnson(G, weight='weight') 
  34. print(paths) 

约翰逊(Johnson)的算法使用示例

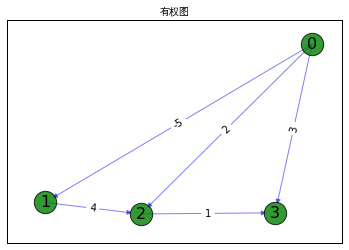
输出:

  1. {'2': {'2': ['2'], '3': ['2', '3']}, '3': {'3': ['3']}, '0': {'2': ['0', '1', '2'], '3': ['0', '1', '2', '3'], '0': ['0'], '1': ['0','1']}, '1': {'2': ['1', '2'], '3': ['1', '2', '3'], '1': ['1']}} 

11.1.7弗洛伊德算法(Floyd-Warshall)

  1. #使用Floyd算法找到所有对最短路径长度。 
  2. G = nx.DiGraph() 
  3. G.add_weighted_edges_from([('0', '3', 3), ('0', '1', -5),('0', '2', 2), ('1', '2', 4), ('2', '3', 1)]) 
  5. #边和节点信息 
  6. edge_labels = nx.get_edge_attributes(G,'weight')  
  7. labels={'0':'0','1':'1','2':'2','3':'3'} 
  9. #生成节点位置  
  10. pos=nx.spring_layout(G)  
  12. #把节点画出来  
  13. nx.draw_networkx_nodes(G,pos,node_color='g',node_size=500,alpha=0.8)  
  15. #把边画出来  
  16. nx.draw_networkx_edges(G,pos,width=1.0,alpha=0.5,edge_color='b')  
  18. #把节点的标签画出来  
  19. nx.draw_networkx_labels(G,pos,labels,font_size=16)  
  21. #把边权重画出来  
  22. nx.draw_networkx_edge_labels(G, pos, edge_labels)  
  24. #显示graph 
  25. plt.title('有权图',fontproperties=myfont) 
  26. plt.axis('on') 
  27. plt.xticks([]) 
  28. plt.yticks([]) 
  29. plt.show() 
  31. #计算最短路径长度 
  32. lenght=nx.floyd_warshall(G, weight='weight') 
  34. #计算最短路径上的前驱与路径长度 
  35. predecessor,distance1=nx.floyd_warshall_predecessor_and_distance(G, weight='weight') 
  37. #计算两两节点之间的最短距离,并以numpy矩阵形式返回 
  38. distance2=nx.floyd_warshall_numpy(G, weight='weight') 
  40. print(list(lenght)) 
  41. print(predecessor) 
  42. print(list(distance1)) 
  43. print(distance2) 

弗洛伊德算法(Floyd-Warshall)使用示例

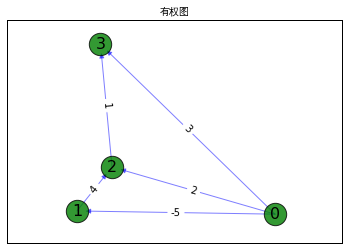
输出:

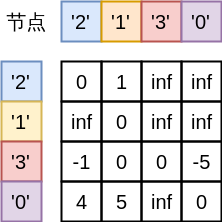
  1. ['2', '3', '0', '1'] 
  2. {'2': {'3': '2'}, '0': {'2': '1', '3': '2', '1': '0'}, '1': {'2': '1', '3': '2'}} 
  3. ['2', '3', '0', '1'] 
  4. [[ 0. 1. inf inf] 
  5. [inf 0. inf inf] 
  6. [-1. 0. 0. -5.] 
  7. [ 4. 5. inf 0.]] 

注:输出中的矩阵不是按照节点0,1,2,3排序,而是2,1,3,0,即如图:


两点之间的最短距离

11.1.8A*算法

  1. G = nx.path_graph(5) 
  3. #显示graph 
  4. nx.draw(G,with_labels=True) 
  5. plt.title('有x向图',fontproperties=myfont) 
  6. plt.axis('on') 
  7. plt.xticks([]) 
  8. plt.yticks([]) 
  9. plt.show() 
  11. #直接输出路径和长度 
  12. print(nx.astar_path(G, 0, 4)) 
  13. print(nx.astar_path_length(G, 0, 4)) 

A*算法

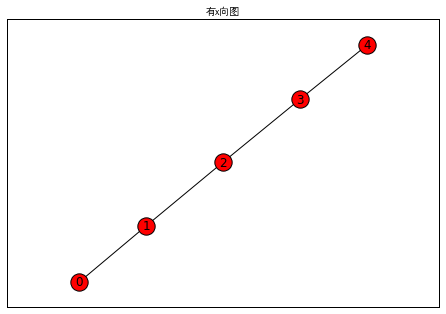
输出:

  1. [0, 1, 2, 3, 4] 
  2. 4 

NetworkX系列教程(10)-算法之一:最短路径问题的更多相关文章

  1. NetworkX系列教程(10)-算法之五:广度优先与深度优先

    小书匠Graph图论 重头戏部分来了,写到这里我感觉得仔细认真点了,可能在NetworkX中,实现某些算法就一句话的事,但是这个算法是做什么的,用在什么地方,原理是怎么样的,不清除,所以,我决定先把图 ...

  2. NetworkX系列教程(10)-算法之四:拓扑排序与最大流问题

    小书匠Graph图论 重头戏部分来了,写到这里我感觉得仔细认真点了,可能在NetworkX中,实现某些算法就一句话的事,但是这个算法是做什么的,用在什么地方,原理是怎么样的,不清除,所以,我决定先把图 ...

  3. NetworkX系列教程(10)-算法之三:关键路径问题

    小书匠Graph图论 重头戏部分来了,写到这里我感觉得仔细认真点了,可能在NetworkX中,实现某些算法就一句话的事,但是这个算法是做什么的,用在什么地方,原理是怎么样的,不清除,所以,我决定先把图 ...

  4. NetworkX系列教程(10)-算法之二:最小/大生成树问题

    小书匠 Graph 图论  重头戏部分来了,写到这里我感觉得仔细认真点了,可能在NetworkX中,实现某些算法就一句话的事,但是这个算法是做什么的,用在什么地方,原理是怎么样的,不清除,所以,我决定 ...

  5. NetworkX系列教程(9)-线性代数相关

    小书匠 Graph 图论  学过线性代数的都了解矩阵,在矩阵上的文章可做的很多,什么特征矩阵,单位矩阵等.grpah存储可以使用矩阵,比如graph的邻接矩阵,权重矩阵等,这节主要是在等到graph后 ...

  6. NetworkX系列教程(2)-graph生成器

    小书匠Graph图论 本节主要讲解如何快速使用内置的方法生成graph,官方的文档在这里,里面包含了networkX的所有graph生成器,下面的内容只是我节选的内容,并将graph画出来而已. 声明 ...

  7. NetworkX系列教程(1)-创建graph

    小书匠Graph图论 研究中经常涉及到图论的相关知识,而且常常面对某些术语时,根本不知道在说什么.前不久接触了NetworkX这个graph处理工具,发现这个工具已经解决绝大部分的图论问题(也许只是我 ...

  8. HTML5游戏开发系列教程10(译)

    原文地址:http://www.script-tutorials.com/html5-game-development-lesson-10/ 最后我们将继续使用canvas来进行HTML5游戏开发系列 ...

  9. Python Twisted系列教程10：增强defer功能的客户端

    作者:dave@http://krondo.com/an-introduction-to-asynchronous-programming-and-twisted/ 译者:杨晓伟(采用意译) 可以从这 ...

随机推荐

  1. Scratch（三）剪刀石头布

    经过上一讲的突击训练,我们从门外汉开始走向编程的深坑,我们今天还要对上一讲的游戏进行加强. 上一个游戏还能演变成什么游戏呢? 我其实知道你们想到的是老hu机什么的,确实,上一个游戏改改可以变成老hu机 ...

  2. Spring AOP日志实现（二）--获取访问者IP及访问路径

    获取类及方法上的@RequestMapping注解: 应该是不等于: 获取访问者的ip地址,首先配置一个监听器: 配置完监听器后,就可以在类中注入一个HttpServletRequest: 获取ip:

  3. HttpClient 远程接口调用方式

    远程接口调用方式HttpClient 问题:现在我们已经开发好了接口了,那该如何调用这个接口呢? 答:使用Httpclient客户端.   Httpclient简介 什么是httpclient Htt ...

  4. 文件流FileStream的读写

    1.FileStream文件流的概念: FileStream 类对文件系统上的文件进行读取.写入.打开和关闭操作,并对其他与文件相关的操作系统句柄进行操作,如管道.标准输入和标准输出.读写操作可以指定 ...

  5. 在Eclipse配置Tomcat服务器+JSP实例创建

    欢迎任何形式的转载,但请务必注明出处. 1.jdk安装及环境配置 点击进入教程 2.Eclipse安装 点击进入官网下载 注意下载完成打开.exe后,出现的界面,有很多版本供选择.选择下图版本 3.T ...

  6. 关于lock和synchronized的选择

    这里不介绍具体用法,介绍lock和synchronized的不同从而做出选择 1.lock是一个接口,而synchronized是java中的一个关键字,synchronized是内置的语言实现. 2 ...

  7. Oracle表空间满处理方式

    一.查询表空间常规语句 1.查询表空间使用情况 SELECT Upper(F.TABLESPACE_NAME)         "表空间名", D.TOT_GROOTTE_MB   ...

  8. C#-FileHelper

    using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.T ...

  9. JAVA 判断给定目录的大小

    题目:给定一个目录,判断该目录的大小,单位为G 思路: 递归拿到目录的子文件,然后取长度,累加 public class FileDemo02 { public static void main(St ...

  10. jmeter+jenkins 配置过程（很详细）

    一.安装jmeter 第一步  安装JDK,配置JDK路径.注:jdk下载地址,推荐使用jdk1.8版本 http://www.oracle.com/technetwork/java/javase/d ...