简析P和NP问题的概念

简析P和NP问题的概念

本文系作者学习笔记，内容均来源于网络，如有侵权，请联系删除

1. P类问题：所有能用多项式时间算法计算得到结果的问题，称为多项式问题，也就是P(polynomial)。

   多项式时间举例：

   

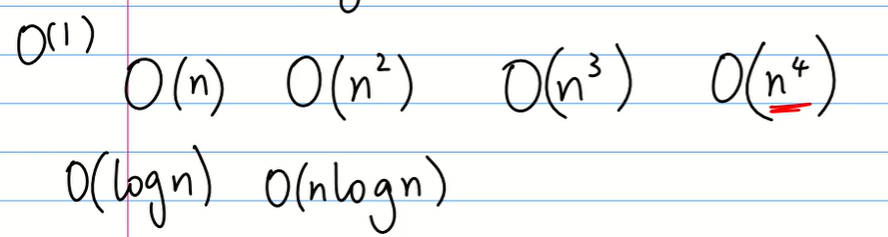
2. NP类问题(Non-Deterministic Polynomial Problems)：NP问题是指存在多项式算法能够验证的非决定性问题

   NP概念的奥妙在于，它躲开了求解到底需要多少时间这样的问题，而仅仅只是强调验证需要多少时间

   显然，P肯定是NP，因为你既然能用多项式求解，就肯定能用多项式验证（难不成我再算一遍就好了嘛！）

   所以，一个问题很有可能同时是P类问题，也是NP类问题（因为P问题就是NP问题的子集啊）

3. NP完全(NP Complete)问题，也叫做NPC问题：一个属于NP类的问题，但目前为止没办法在P时间内解决（也就是说目前只能在P时间内判断解的正确性）

   • 一个经典的NP完全问题：3-SAT问题

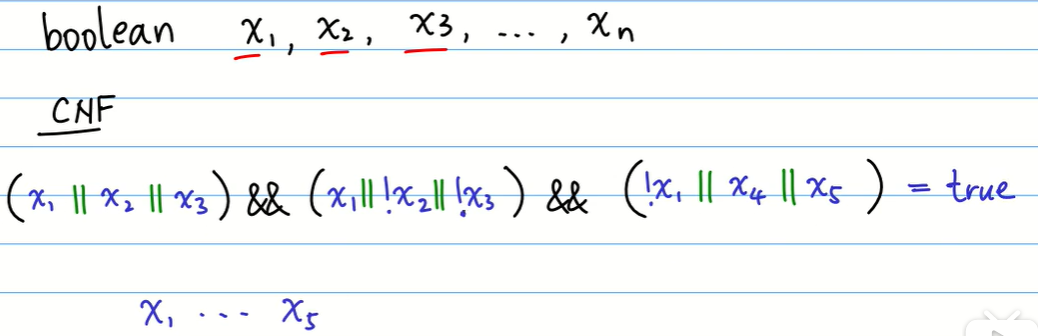
是否存在一种组合，使得结果最终等于True

需要注意的是，所有的NP完全问题是可以互相转换的。

• 一个经典的NP完全问题：完全图问题：

从图中找到k个节点组成的完全子图。也是只能在多项式时间内验证，目前还没办法证明。

拿到这个问题之后，我们可以试着将这个问题转换为3-SAT问题，这样就能说明它就是NP完全问题了（就可能偷懒不去试着解决问题了23333）

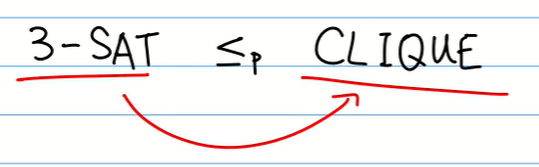
图中这个符号表示3-SAT问题可以在多项式时间内转换为CLIQUE问题（也就是我们所说的完全图问题），当然谁转谁都行的····

1. 这里所用的3-SAT问题场景
   

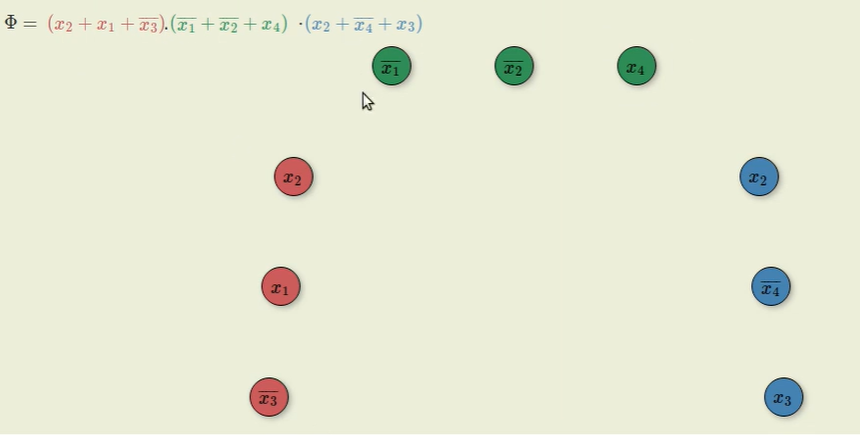
下面节点的颜色代表括号的分组

1. 将每个点连接到其他组中除了和自己相反的变量之外所有的变量，自己组内的也不连

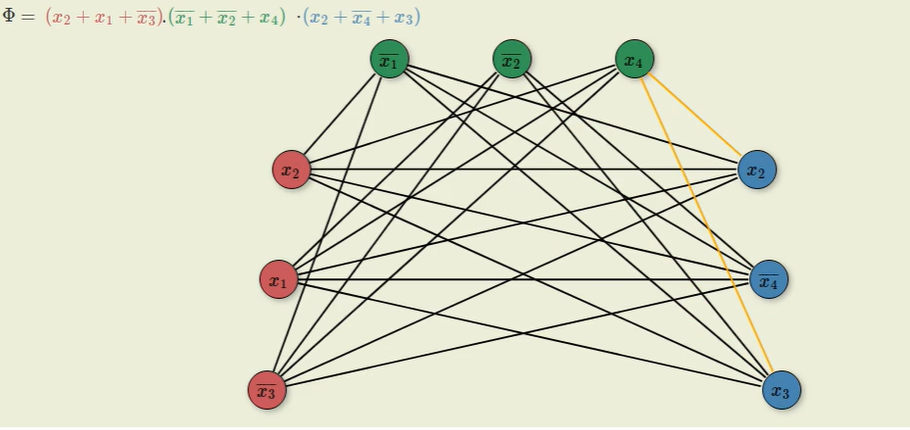
1. 设置k等于3-SAT问题中括号的数量

如果这里能找到这样一个有k个节点的回路，就表示上面的3-SAT问题是有解的。

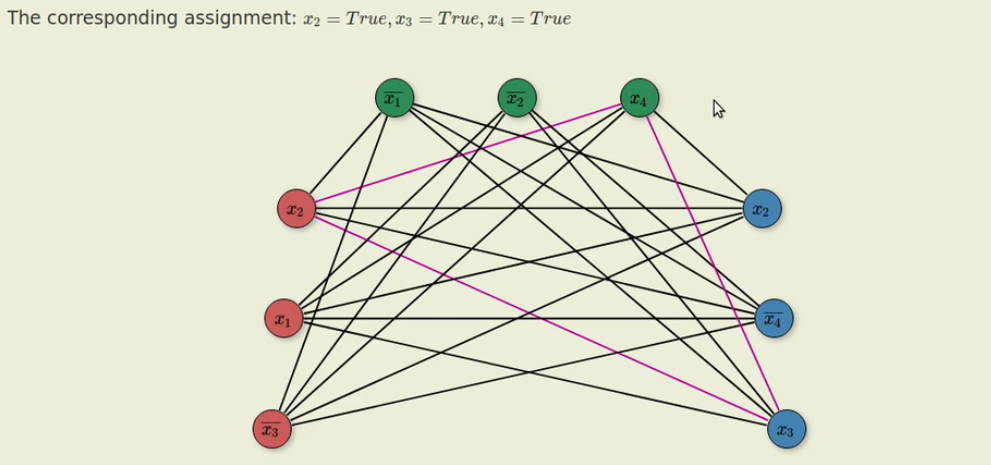
如图，只要把X2\X4\X3设为True，则原3-SAT问题有解为什么这种方式是合理的呢？因为原来的3-SAT问题最核心的问题所在就是设置变量为True时会导致这个变量的反值为False，这样就有可能造成某一个括号中为False。而由于我们在连接各个节点时没有连接1. 本身集合中的值2.该变量的反值。使得连接成的回路中的节点一定是来自不同的集合中且不会同时存在某一个变量和其反值的。那么将这样的回路中的节点值设为True就一定能解决问题了。

1. 目前没有解决的命题:P是否等于NP，也就是是否存在一个问题，只能用P时间检验，不能用P时间求解。目前大家倾向于P不等于NP，但是并没有证明出来

2. NP难问题(NP-hardness problem):如果所有NP问题都可以多项式时间归约到某个问题，则称该问题为NP困难。

   NP难问题的特征是至少和NP问题一样难

   这里涉及一个概念，不妨称为问题之间的归约。可以认为各个问题的难度是不同的，表现形式为，如果我可以把问题A中的一个实例转化为问题B中的一个实例，然后通过解决问题B间接解决问题A，那么就认为B比A更难。

   通过对归约过程做出限制可以得到不同类型的归约。复杂度理论里经常用到的规约叫polynomial-time Karp' reduction。其要求是转化问题的过程必须是多项式时间内可计算的。

   称问题L是NP-hard，如果任意一个NP的问题都可以多项式规约到L。如果一个NP-hard的问题L本身就是NP的，则称L是NP-complete。这个定义可以推广到所有复杂度类。所以NPcompleness的直观解释就是，我能解决这个问题就相当于具备了用相同级别的计算资源解决这个复杂度类里所有问题的能力。

   一个NP问题可以在多项式时间内规约到问题L中，说明L的难度是要高于原问题的，由于是“任意一个NP问题都可以规约”，所以说L的难度是不低于所有NP问题的。而如果这个L依然是NP问题，而不是连NP的程度都达不到的话，我们就可以说它应该是NP中最难的那一种了，也就是NP完全问题了。由于NP完全问题算是NP问题中最难的那一种了，而且搁目前也没办法在P时间内解决，所以可以说NP完全问题之间的难度是一样的了，NP完全问题之间可以互相转化也验证了这一点。

Reference

1. https://blog.csdn.net/bitcarmanlee/article/details/51935400
2. https://www.bilibili.com/video/av16446193?from=search&seid=1193870537063836496
3. http://www.voidcn.com/article/p-yfvjdvmq-nh.html