bzoj 1001狼抓兔子（对偶图+最短路）最大流

推荐文章：《浅析最大最小定理在信息学竞赛中的应用》--周冬

题目

现在小朋友们最喜欢的"喜羊羊与灰太狼",话说灰太狼抓羊不到，但抓兔子还是比较在行的，
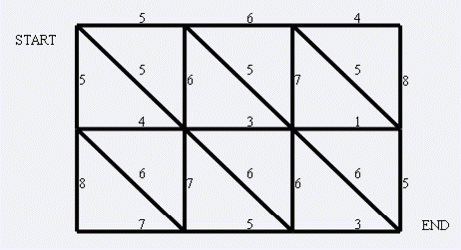
而且现在的兔子还比较笨，它们只有两个窝，现在你做为狼王，面对下面这样一个网格的地形：
 
左上角点为(,),右下角点为(N,M)(上图中N=,M=).有以下三种类型的道路
:(x,y)<==>(x+,y)
:(x,y)<==>(x,y+)
:(x,y)<==>(x+,y+)
道路上的权值表示这条路上最多能够通过的兔子数，道路是无向的. 左上角和右下角为兔子的两个窝，
开始时所有的兔子都聚集在左上角(,)的窝里，现在它们要跑到右下解(N,M)的窝中去，狼王开始伏击
这些兔子.当然为了保险起见，如果一条道路上最多通过的兔子数为K，狼王需要安排同样数量的K只狼，
才能完全封锁这条道路，你需要帮助狼王安排一个伏击方案，使得在将兔子一网打尽的前提下，参与的
狼的数量要最小。因为狼还要去找喜羊羊麻烦.
Input
 
第一行为N,M.表示网格的大小，N,M均小于等于1000.
接下来分三部分
第一部分共N行，每行M-1个数，表示横向道路的权值.
第二部分共N-1行，每行M个数，表示纵向道路的权值.
第三部分共N-1行，每行M-1个数，表示斜向道路的权值.
输入文件保证不超过10M
Output
 
输出一个整数，表示参与伏击的狼的最小数量.
 
Sample Input
 
Sample Output

题目图片

讲这部分之前，请先阅读以上的文章（讲得十分好%%%）（当然阅读到27页就好了）

读完后，我们发现这道题完全可以用其对偶图来跑最短路。

原图                                 对偶图

面数 x                              面数 y

点数 y   那么其对偶图中      点数 x

边数 z                               边数 z

面数和点数正好相反。

将原图的起点和终点连接起来，建立一个新的面（这是必须的）。

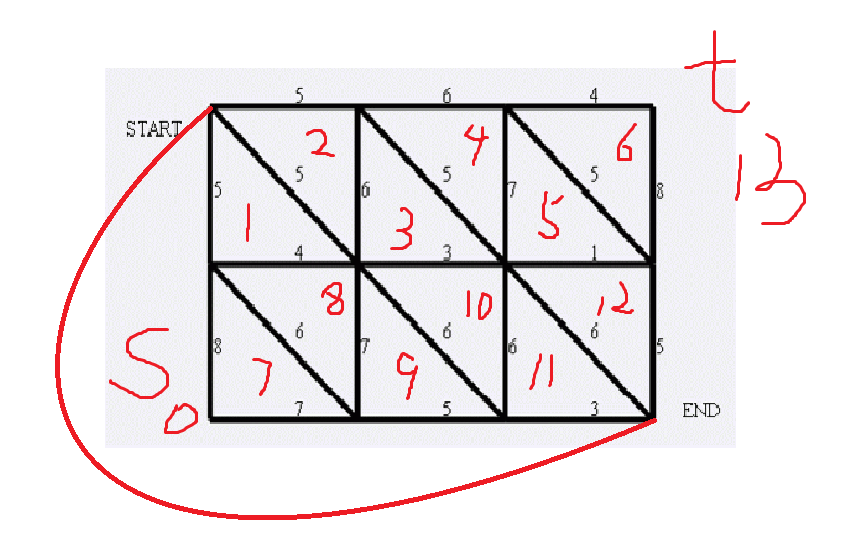
当然s点和t点之间是没有边的。

s和1,7,9,11之间有边。

t和2,4,6,12之间有边。

上面是我们建好的对偶图，从左至右依次编号，关于对偶图中面的编号，因为我们是按照横边，纵边，斜边的顺序读入的，所以我们一定要按照一定的方法对这些图编号

我采用的是从左至右依次编号，因为我们可以很清楚当前边连接的两个点（原图中的两个面）所在的位置，因为这是平面图，所以可以用欧拉公式来求出之前有多少点（

原图中的面）。再加上这个点（原图中的面（重要的事说三遍））在当前行中的位置就是它的编号。

只要原图中的两个面之间存在边，那么它的对偶图中的两个点就存在边。

#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
int cnt, i, j, x, xx, xxx, h, t, s, hh[], n, m, w;
bool dd[];
int e, l[], d[], hhh, ww;
struct node
{
    int v, next, z;
} b[];
inline void add(int aa, int bb, int cc)//邻接表，建双向边
{
    b[++cnt].v = bb;
    b[cnt].next = hh[aa];
    b[cnt].z = cc;
    hh[aa] = cnt;
    b[++cnt].v = aa;
    b[cnt].next = hh[bb];
    b[cnt].z = cc;
    hh[bb] = cnt;
}
void add1()
{
    for(i = ; i < m; ++i)
    {
        scanf("%d", &x);
        add(i * , t, x);
    }
    for(i = ; i < n; ++i)
    {
        for(j = ; j < m; ++j)
        {
            scanf("%d", &x);
            add((i - ) * (m - ) *  + j * , (i - ) * (m - ) *  + j *  - m *  + , x);//利用欧拉公式确定编号并建边(下面的add函数也是如此)
        }
    }
    for(j = ; j < m; ++j)
    {
        scanf("%d", &x);
        add(s, (n - ) *  * (m - ) + j *  - , x);
    }
}
void add2()
{
    for(i = ; i < n; ++i)
    {
        scanf("%d", &x);
        xx = (i - ) * (m - ) *  + ;
        add(s, xx, x);
        for(j = ; j < m; ++j)
        {
            scanf("%d", &x);
            xx += ;
            add(xx - , xx, x);
        }
        scanf("%d", &x);
        add(xx + , t, x);
    }
}
inline void add3()
{
 
    for(i = ; i < n; ++i)
    {
        for(j = ; j < m; ++j)
        {
            scanf("%d", &x);
            add((i - ) * (m - ) *  + j * , (i - ) * (m - ) *  + j *  - , x);
        }
    }
}
//下面的spfa中一定要用循环队列，省空间。不用的话空间开小（这很有可能毕竟1百万个点）可能会被卡。
void spfa()
{
    dd[s] = true;
    h = ;
    w = ;
    memset(l,0x3f,sizeof(l));//将l数组赋成最大值
    //hhh记录的是我们用的是队列中第几个元素（实际上）
    //ww记录的是队列中总共有几个元素
    l[s] = ;
    while()
    {
        if(hhh > ww)break;
        h = hhh % ;
        w = ww % ;
        for(i = hh[s]; i; i = b[i].next)
        {
            e = b[i].v;
            if(l[s] + b[i].z < l[e])
            {
                l[e] = l[s] + b[i].z;
                if(!dd[e])w = ww % , d[++w] = e, ww++, dd[e] = true;
            }
        }
        dd[s] = false;
        h = hhh % ;
        s = d[++h];
        hhh++;
    }
}
int main()
{
    scanf("%d %d", &n, &m);
    if(n == m && n == )//特判
    {
        printf("");
        return ;
    }
    s = ;
    t =  * (n - ) * (m - ) + ;
    add1();//读入横边
    add2();//读入纵边
    add3();//读入斜边
    spfa();//对其对偶图求s————t的最短路
    printf("%d", l[t]);
    return ;
}