LG P2822 NOIP2016D2T1 组合数问题

一句话题意

给定n、m和k，求对于所有的i(0<=i<=n)和j(0<=j<=min(i,m))，有多少对(i,j)使\(C_i^j\)使k的倍数

数据范围

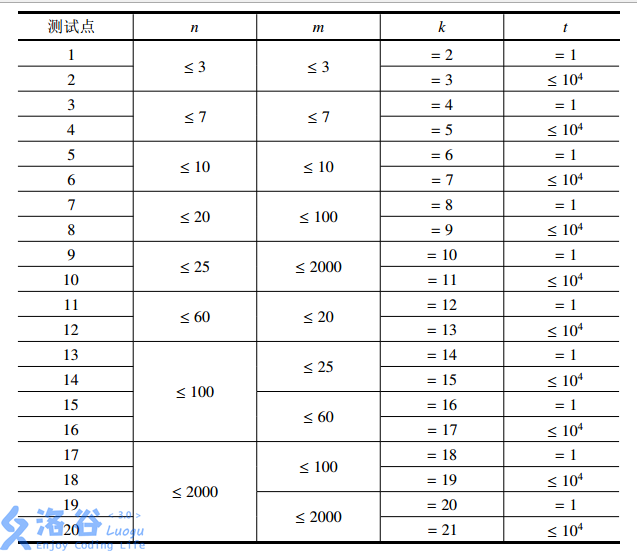
部分分、满分做法和思路

30pts

直接暴力套公式（不用杨辉三角）

90pts

杨辉三角+二分。

具体实现：用vectorv[2005],v[i]中的元素j都是使得(i,j)可以满足要求的j。那么给定n、m后，枚举n，二分m即可。

代码：

#include<bits/stdc++.h>
using namespace std;
int T,k,c[2005][2005];
vector<int>v[2005];
int main()
{
	scanf("%d %d",&T,&k);
	c[0][0]=c[1][0]=c[1][1]=1;
	for(int i=2;i<=2000;i++)
	{
		for(int j=0;j<=2000;j++)
		{
			c[i][j]=(c[i-1][j]+c[i-1][j-1])%k;
			if(c[i][j]%k==0) v[i].push_back(j);
		}
	}
	while(T--)
	{
		int n,m;
		scanf("%d %d",&n,&m);
		int ans=0;
		for(int i=2;i<=n;i++)
		{
			if(v[i].size()==0) continue;
			int endd=min(m,i);
			int l=0,r=v[i].size()-1,mid,tans=-1;
			while(l<=r)
			{
				mid=(l+r)/2;
				if(v[i][mid]>endd) r=mid-1;
				else l=mid+1,tans=mid;
			}
			ans+=tans+1;
		}
		printf("%d\n",ans);
	}
	return 0;
}

100pts

(其实上面那种做法在我的电脑上能A。。但洛谷上T了两个点。不知道CCF少爷机会怎么样）

二分仍然太慢。让我们考虑预处理+O(1)回答每个询问的方法：前缀和（二维的）

用qian[i][j]表示n=i,m=j时有多少组解满足要求。很好实现。(r数组是辅助数组，r[i][j]表示n=i时的一维前缀和)

#include<bits/stdc++.h>
using namespace std;
int T,k,c[2005][2005],qian[2005][2005],r[2005][2005];
bool ok[2005][2005];
//vector<int>v[2005];
int main()
{
	scanf("%d %d",&T,&k);
	c[0][0]=c[1][0]=c[1][1]=1;
	for(int i=2;i<=2000;i++)
	{
		for(int j=0;j<=i;j++)
		{
			c[i][j]=(c[i-1][j]+c[i-1][j-1])%k;
			if(c[i][j]%k==0) ok[i][j]=1;
		}
	}
	for(int i=1;i<=2000;i++)
	{
		r[i][0]=ok[i][0];
		for(int j=1;j<=2000;j++)
		{
			r[i][j]=r[i][j-1]+ok[i][j];
		}
	}
	for(int i=1;i<=2000;i++)
	{
		for(int j=0;j<=2000;j++)
		{
			qian[i][j]=qian[i-1][j]+r[i][j];
		}
	}
	while(T--)
	{
		int n,m;
		scanf("%d %d",&n,&m);
		/*int ans=0;
		for(int i=2;i<=n;i++)
		{
			if(v[i].size()==0) continue;
			int endd=min(m,i);
			int l=0,r=v[i].size()-1,mid,tans=-1;
			while(l<=r)
			{
				mid=(l+r)/2;
				if(v[i][mid]>endd) r=mid-1;
				else l=mid+1,tans=mid;
			}
			ans+=tans+1;
		}*/
		printf("%d\n",qian[n][m>n?n:m]);
	}
	return 0;
}