Mathematically Hard LightOJ-1007（欧拉定理+前缀和）

Description

Mathematically some problems look hard. But with the help of the computer, some problems can be easily solvable.

In this problem, you will be given two integers a and b. You have to find the summation of the scores of the numbers from a to b (inclusive).

The score of a number is defined as the following function.score (x) = n², where n is the number of relatively prime numbers with x, which are smaller than x

For example,

For 6, the relatively prime numbers with 6 are 1 and 5. So, score (6) = 2² = 4.

For 8, the relatively prime numbers with 8 are 1, 3, 5 and 7. So, score (8) = 4² = 16.

Now you have to solve this task.

Input

Input starts with an integer T (≤ 10⁵), denoting the number of test cases.Each case will contain two integers a and b (2 ≤ a ≤ b ≤ 5 * 10⁶).

Output

For each case, print the case number and the summation of all the scores from a to b.

Sample Input

6

8 8

2

Sample Output

Case 1: 4

Case 2: 16

Case 3: 1237

Note

Euler's totient function  applied to a positive integer ø(n) is defined to be the number of positive integers less than or equal to ø(n) that

are relatively prime to ø(n).  is read "phi of n."Given the general prime factorization of 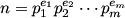 , one can compute ø(n)using the formula

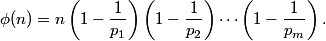
在数论中，对正整数n，欧拉函数  是小于或等于n的正整数中与n互质的数的数目,对欧拉函数打表;

注意 ：long long 需要用无符号型；

代码如下：

#include<iostream>
#include<cstdio>
using namespace std;
typedef unsigned long long ll;
const int maxx=;
ll a[maxx];
void init()
{
    for(int i=; i<maxx; i++)
        a[i]=i;
    for(int i=; i<maxx; i++)
    {
        if(a[i]==i)
        {
            for(int j=i; j<maxx; j+=i)
                a[j]=a[j]/i*(i-);
        }
    }
    for(int i=; i<maxx; i++)
        a[i]=a[i]*a[i]+a[i-];
}
int main()
{
    init();
    int t,Case=;
    cin>>t;
    while(t--)
    {
        int n,m;
        cin>>n>>m;
        printf("Case %d: ",++Case);
        cout<<a[m]-a[n-]<<endl;
    }
    return ;
}