ACM课内练习_1

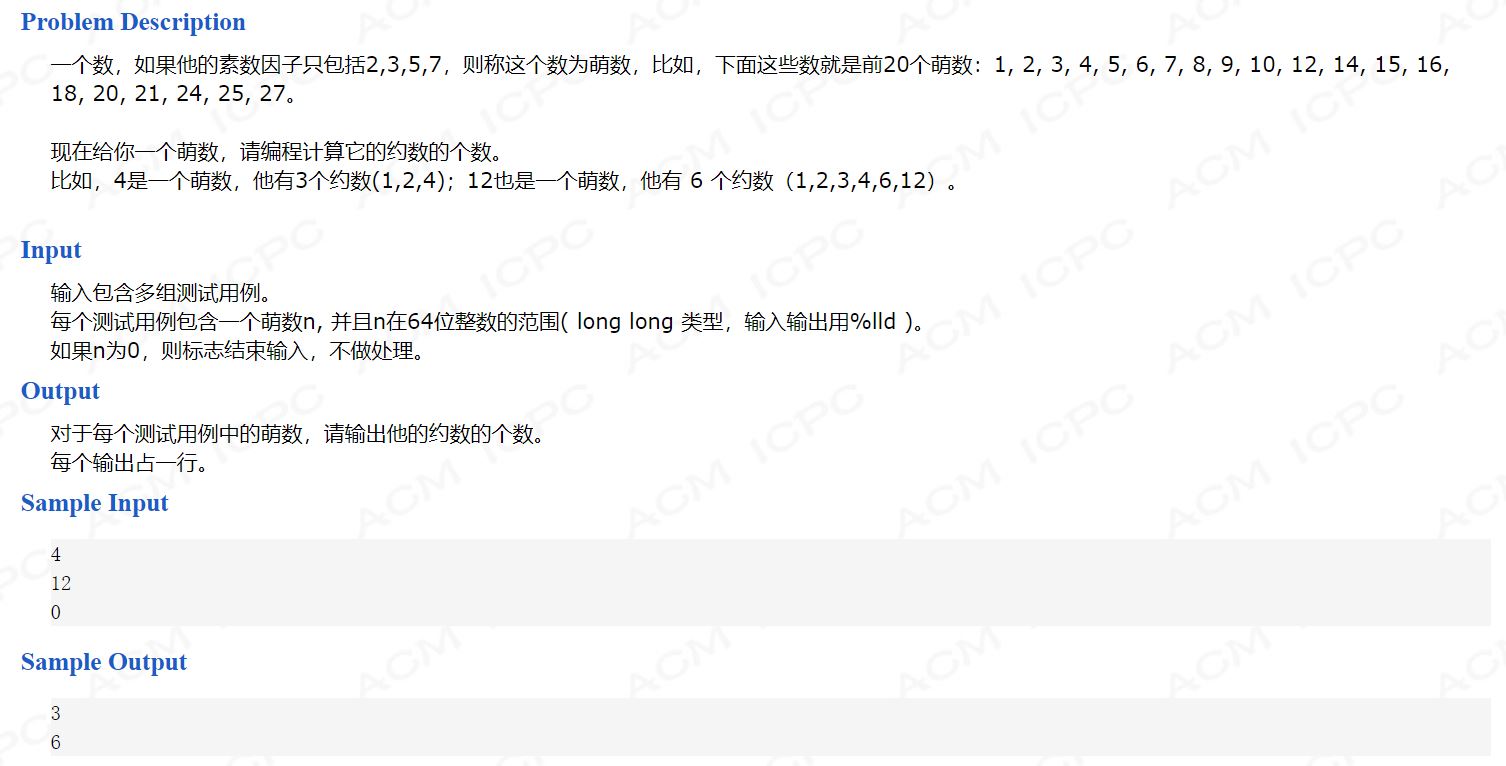
题意很简单就是一个一个素数因子只有2,3,5,7的整数,让你求它的约束的个数(暴力会超时),一开始的思路是先计算2,3,5,7这四个素数因子的个数,求出来之后想了很久没有想出他们个数和约束个数之间的数学关系,后来看了别人的代码,自己画了张图分析了一下,将2,3,5,7的个数全部加上1之后的四个数的乘积就是约数的个数(可以画棵树分析一下)

例如:12=2*2*3

1.从根部1出发,两个素因数2,所以有三种可能

一个二都不乘: 1

乘一个二: 2

乘两个二: 4

2.然后从 1,2,4 出发 ,有6种可能

1,2,4每个两种,要么保持原来的值不变,要么乘以3

也就是1,3 2,6 4,12 这六种情况

  while (scanf("%I64d", &n), n)
     {
         Int num[] = {, , , };
         int ans[] = {, , , };//由在算的时候没有把0个2，0个3，0个5或者0个7的情况计算进去，所以一开始就加上
         for (int i = ; i < n; i++)
         {
             while (n !=  && n % num[i] == )//算出2，3，5，7的个数
             {
                 ans[i]++;
                 n /= num[i];
             }
         }
         printf("%d\n", ans[] * ans[] * ans[] * ans[]);
     }

链接:https://blog.csdn.net/weixin_42165786/article/details/80318236