转：解释lsh

Locality sensitive hashing — LSH explained

The problem of finding duplicate documents in a list may look like a simple task — use a hash table, and the job is done quickly and the algorithm is fast. However, if we need to find not only exact duplicates, but also documents with differences such as typos or different words, the problem becomes much more complex. In my case, I’ve had to find duplicates in a very long list of given questions.

Jaccard index

First, we need to define a method of determining whether a question is a duplicate of another. After experimenting with string distance metrics (Levenshtein, Jaro-Winkler, Jaccard index) I’ve come to the conclusion that the Jaccard index performs sufficiently for this use case. The Jaccard index is an intersection over a union. We count the amount of common elements from two sets, and divide by the number of elements that belong to either the first set, the second set, or both. Let’s have a look at the example:

Assuming that we have two following questions:

“Who was the first ruler of Poland”

“Who was the first king of Poland”

We can visualize it in the following sets:

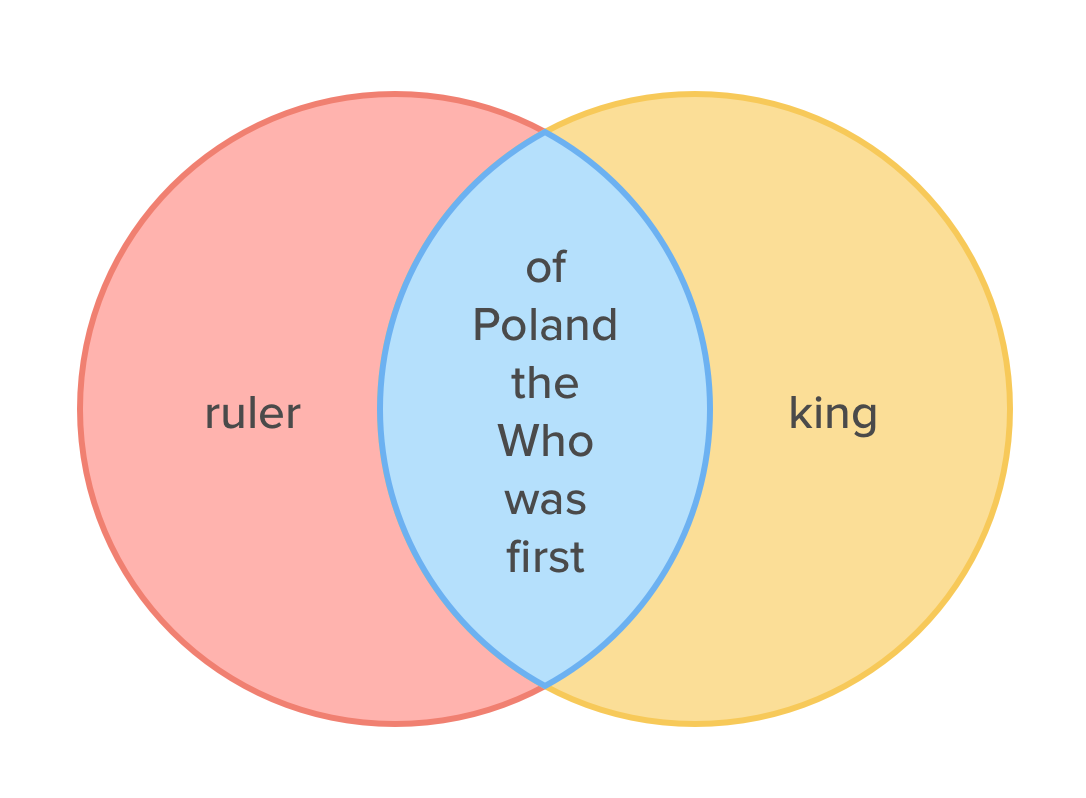
The size of the intersection is 6, while the size of the union is 6 + 1 + 1 = 8, thus the Jaccard index is equal to 6 / 8 = 0.75

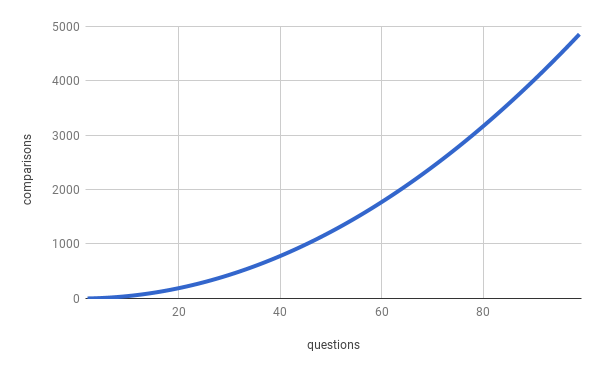
We can conclude — the more common words, the bigger the Jaccard index, the more probable it is that two questions are a duplicate. So where we can set a threshold above which pairs would be marked as a duplicate? For now, let’s assume 0.5 as a threshold, but in a real life, we need to get this value by experiment. We could stop here, but current solution makes a number of comparisons growing quadratically (It’s 0.5*(n²-n) where n is the number of questions).

Min part of MinHash

It’s been shown earlier that the Jaccard can be a good string metric, however, we need to split each question into the words, then, compare the two sets, and repeat for every pair. The amount of pairs will grow rapidly. What if we somehow created a simple fixed-size numeric fingerprint for each sentence and then just compare the fingerprints?

In this section I will use following questions:

“Who was the first king of Poland”

“Who was the first ruler of Poland”

“Who was the last pharaoh of Egypt”

And their Jaccard indexes:

J(“Who was the first king of Poland”, “Who was the first ruler of Poland”) = 0.75

J(“Who was the first king of Poland”,“Who was the last pharaoh of Egypt”) = 0.4

J(“Who was the first ruler of Poland”, “Who was the last pharaoh of Egypt”)=0.4

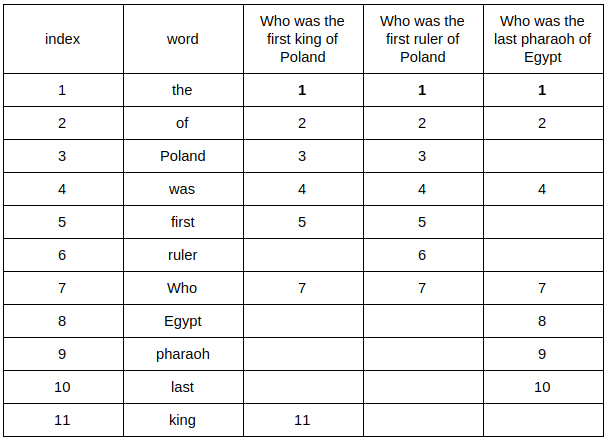
To calculate MinHash we need to create the dictionary (a set of all words) from all our questions. Then, create a random permutation:

(“last”, “Who”, “Egypt”, “king”, “ruler”, “was”, “of”, “Poland”, “pharaoh”, “the”, “first”)

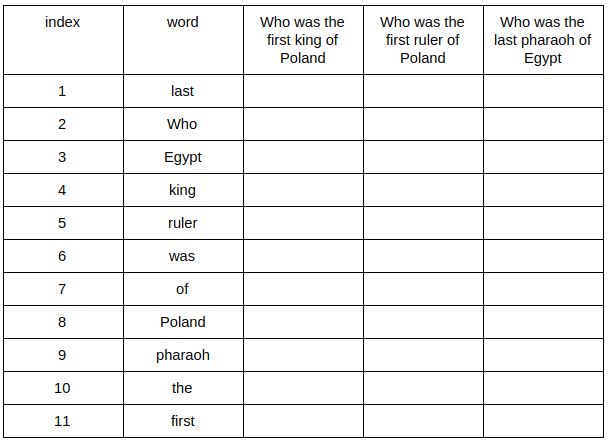
We have to iterate over the rows, writing the index in the respective cell, if the word being checked is present in the sentence.

Now the second row:

And the rest:

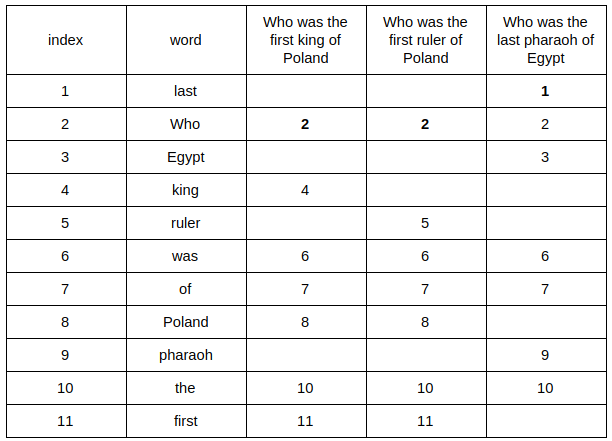
Only the first word occurrence is relevant (giving a minimal index — hence the name MinHash). We have a minimum value for all our questions and the first part of the fingerprint. To get the second one we need to create another random permutation and retrace our steps: /////只有出现的第一个单词是相关的(给出最小索引，因此命名为MinHash)。我们对所有的问题和指纹的第一部分都有一个最小值。为了得到第二个，我们需要创建另一个随机排列，并返回我们的步骤

Then, we repeat permuting and searching as many times as big we want our fingerprint. For the purpose of example my consists of 6 items. We’ve already had 2, so let’s create 4 more permutations:

(“first”, “king”, “Egypt”, “was”, “Who”, “of”, “pharaoh”, “last”, “Poland”, “ruler”, “the”)

(“ruler”, “king”, “Poland”, “Who”, “the”, “pharaoh”, “of”, “first”, “Egypt”, “last”, “was”)

(“king”, “Poland”, “ruler”, “last”, “pharaoh”, “the”, “Who”, “Egypt”, “first”, “of”, “was”)

(“the”, “pharaoh”, “Who”, “ruler”, “Poland”, “Egypt”, “king”, “last”, “was”, “first”, “of”)

Our complete MinHashes are:

MinHash(“Who was the first king of Poland”) = [2, 1, 1, 2, 1, 1]

MinHash(“Who was the first ruler of Poland”) = [2, 1, 1, 1, 1, 1]

MinHash(“Who was the last pharaoh of Egypt”) = [1, 1, 3, 4, 4, 1]

Now we can check how similar are two MinHashes by calculating their Jaccard indexes:

MinHashSimilarity(“Who was the first king of Poland”, “Who was the first ruler of Poland”) = 5/6 ≈ 0.83

MinHashSimilarity(“Who was the first king of Poland”, “Who was the last pharaoh of Egypt”) = 2/6 ≈ 0.33

MinHashSimilarity(“Who was the first ruler of Poland”, “Who was the last pharaoh of Egypt”) = 2/6 ≈ 0.33

Well, that’s really close to their Jaccard indexes, and the more permutations we do, the closer the approximations get. How’s that possible?

Let’s analyze how we calculate the Jaccard index. We need to look at our table. Considering only two questions, we can create a table like the following:

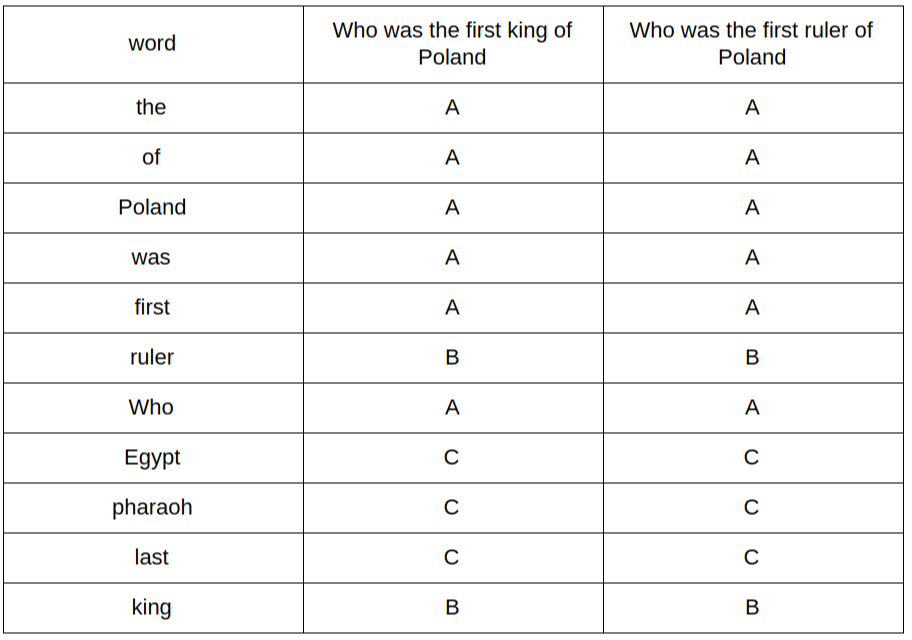
A — where the word is present in both questions

B —it’s present in one of them

C — it’s in the dictionary, but in neither of the questions

We can write the formula for the Jaccard index as a/(a+b) where a is a number of rows of type A and b of type B

Now since we have random permutations, let’s count a probability that two questions will have an equal fingerprint component. We can skip type C rows since they do not interfere in any way with a component value calculation (If we consider only two questions). So what is the probability that we will take type A row, from the set of A and B rows? P = a/(a + b) which is exactly the same as Jaccard index! That explains why our approximations were close and why more permutations mean better approximations.

Hash part of MinHash

We now have an algorithm which could potentially perform better, but the more documents the bigger the dictionary, and thus the higher the cost of creating permutations, both in time and hardware. Instead of creating n permutations we can take a hash function (like md5, sha256 etc.) use it on every word in the question and find a minimal hash value. It will be the first element of the fingerprint, then we will take another hash function, and so on until we have our n elements in the fingerprint. Wait, but why does it work?

Let’s wonder what permutation does — it basically maps each word from dictionary to a different number. The fact that mapped numbers are integers increased by one is not important to us.

What are hash functions doing? Simplifying — they map string to a number, so basically the same as the permutation! How is that better? We don’t need the whole dictionary before — if the new question appears we can easily calculate its MinHash. Also, we don’t need to scan the whole dictionary for each question and create a permutation of the whole dictionary. Both of these operations are pretty costly. We just saved a lot of our and our’s computer time.

So now we can compute a fingerprint and compare it easily, but still we need to compare every fingerprint with all others. This is bad. Exponentially bad.

LSH

Let’s look back at our MinHashes:

MinHash(“Who was the first king of Poland”) = [2, 1, 1, 2, 1, 1]

MinHash(“Who was the first ruler of Poland”) = [2, 1, 1, 1, 1, 1]

MinHash(“Who was the last pharaoh of Egypt”) = [1, 1, 3, 4, 4, 1]

Now group them by three elements:

MinHash(“Who was the first king of Poland”) =[2, 1, 1, 2, 1, 1] => [211, 211]

MinHash(“Who was the first ruler of Poland”) =[2, 1, 1, 1, 1, 1] => [211, 111]

MinHash(“Who was the last pharaoh of Egypt”)=[1, 1, 3, 4, 4, 1]=>[113,441]

What can we see? Our duplicates have one common group (first) where unique has no common groups. Since still, we’re talking about probability influenced issue let’s calculate what is the probability of at least one common group for duplicates:

• Probability of one specific element common in fingerprint = Jaccard index = P1 = 0.75
• Probability that all elements in one group are identical = Jaccard index to number of elements in group power = P2 = 0.75³ = 0.421875
• Probability that group will be different = P3 = 1-P2 = 0.578125
• Probability that all groups will be different = P4 to number of groups power = P3² = 0.334228516
• And finally — Probability that at least one group will be common = P5 = 1 — P4 = 0.665771484

So general equation will look like this: P5 = 1 — (1 — Jⁿ⁾b

Where:

J — Jaccard index

n — number of elements in group

b — number of groups

And probability for our unique question is 1 — (1–0.4³)² = 0.123904 — much lower. We could also make 3 groups 2 elements each. Here is plot:

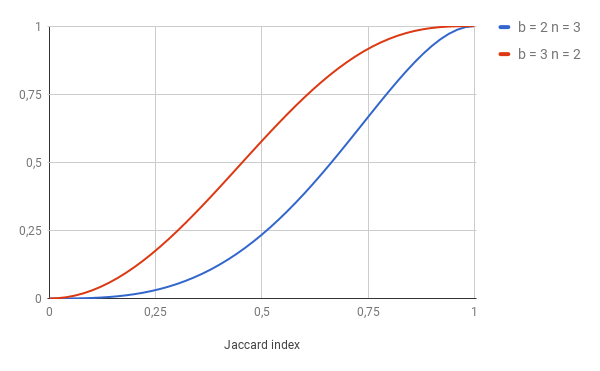
Let’s analyze it: For the pair with J = 0.5 and b = 3, there is only 0.25 probability that we would find it as a duplicate. However, with b = 3 there is about 0.6 probability that we would mark it as a duplicate. What does it mean in practice? — More false positives for b = 3 and more false negatives for b = 2. We need to choose carefully our parameters, but more on that later.

Now we do not need to count anything — if there is a common group we can mark it as duplicates. We can just create lists with single groups:

[211, 211]

[211, 111]

[113, 441]

↓

[

211 => “Who was the first king of Poland”,

211 => “Who was the first ruler of Poland”,

113 => “Who was the last pharaoh of Egypt”

]

And

[

211 => “Who was the first king of Poland”,

111 => “Who was the first ruler of Poland”,

441 => “Who was the last pharaoh of Egypt”

]

It looks familiar to Hashtable! We can put columns of groups in the hash table and check for collision. Collision means that we hit a duplicate. And operations on the hash table have worst case scenario complexity of O(n), so our algorithm (of course depends on implementation) have potential to be also O(n) complex. Way better than O(n²) we had at the beginning.

Tweaking

After what we’ve learned so far we know that LSH takes, 3 arguments:

k — number of elements in MinHash

n — number of elements in groups (or buckets)

b — number of buckets and b*n must equal k

Our goal is to mark as duplicate every pair, or more, that have Jaccard index >= 0.17, so our probability chart should look like this:

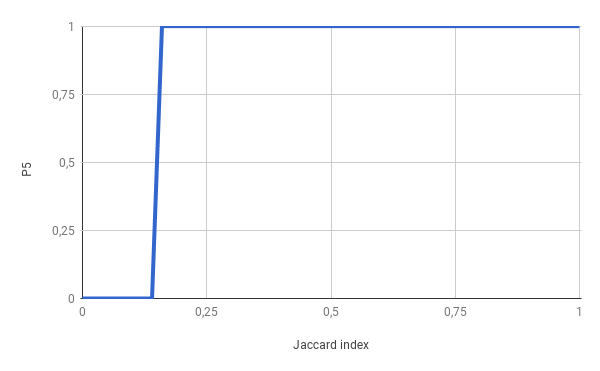
Achieving step function is impossible in our case, so by manipulating our 3 parameters we need to approximate this as close as possible having in mind that bigger the k, more computing power we need (more hashes to calculate). After experiments, I’ve found that 200 for k is good starting value and it also has many divisors. Although 240 has more, so it would be my next shot.

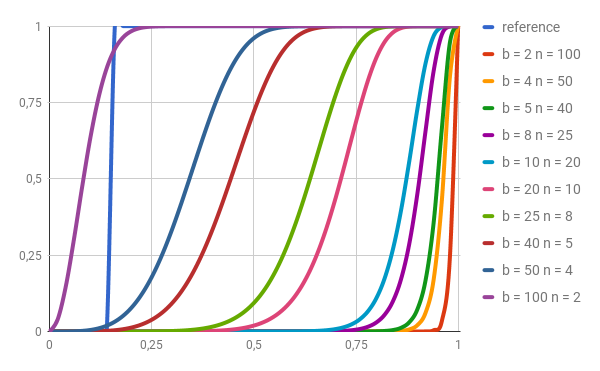
As we can see b = 100 n = 2 or b = 50 n = 4 are the ones closest to reference. We should use both and then compare results.

One thing left — where to get 200 hash functions? Two example solutions:

• use MurmurHash with 200 different seeds
• create our own hash function by taking the output of md5 or another hash function and making XOR with some random number. Example python code:

def myFirstHash(string):

return md5(hash) ^ 636192

def mySecondHash(string):

return md5(hash) ^ 8217622

# And so on.

# But do it in a loop!

Warning — LSH can, and sometimes will produce accidental collisions, so at the end, we still need to compare all questions in given collision but it will be much much fewer operations than comparing all to each other.

And that would be all for now. In next article, I will show example implementation and some benchmarks.

转自：

---

https://medium.com/engineering-brainly/locality-sensitive-hashing-explained-304eb39291e4

Hubert Bryłkowski