python应用 曲线拟合 02

前情提要

---

CsI 闪烁体晶体+PD+前放输出信号满足：

$U(t) = \frac{N_f\tau_p}{\tau_p-\tau_f} \left[ e^{-\frac{t}{\tau_p}}-e^{-\frac{t}{\tau_f}} \right] + \frac{N_s\tau_p}{\tau_p-\tau_s} \left[ e^{-\frac{t}{\tau_p}}-e^{-\frac{t}{\tau_s}} \right] $

其中，U(t) 表示信号输出，电压单位，N 表示闪烁体晶体发出的光中快慢成分的强度，$\tau$ 表示快慢成分的衰减时间，$\tau_p$ 表示前放衰减时间，即前放 RC 常数。

现已有 U(t) 数据，需要拟合给出快慢成分的衰减时间 $\tau$。

实现代码

---

# -*- coding: utf-8 -*-
"""
Created on Mon Jun 15 15:28:17 2020

@author: kurrrr
"""

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit

'''
t_pre :     preamplifier tau
b:     number of fast photons
c:     number of slow photons
p:     tau of fast photons
q:     tau of slow photons
u:     x offset
v:     y offset
'''

t_pre = 26.0

def pre_func_1(x, v):
    return v

def pre_func_2(x, b, c, p, q, u, v):
    global t_pre
    return (b*t_pre/(t_pre-p) *
            (np.exp(-(x-u)/t_pre)-np.exp(-(x-u)/p))
            + c*t_pre/(t_pre-q) *
            (np.exp(-(x-u)/t_pre)-np.exp(-(x-u)/q))
            + v)

def pre_func(x, b, c, p, q, u, v):
    return np.piecewise(x, [x < u, x >= u], [lambda x: pre_func_1(x, v),
                        lambda x: pre_func_2(x, b, c, p, q, u, v)])

alpha_file = open("./gamma_csi.txt", "r")
data_str = alpha_file.read()
data_str = data_str.split()
data = list(map(float, data_str))
x = data[0::2]
y = data[1::2]

popt, pcov = curve_fit(pre_func, x, y, [0.6, 1.2, 1, 1, 2, 0], maxfev=5000)
print(popt)

plt.scatter(x, y, marker='.', label="original data")
y_fit = ([pre_func(xx, popt[0], popt[1], popt[2], popt[3], popt[4], popt[5])
          for xx in x])
plt.plot(x, y_fit, label="Fitted Curve", color='red')
plt.legend(loc='upper right')
plt.show()

# show the fit result
p_str = "Tf = " + str(min(popt[2], popt[3])+0.0005)[:5]
q_str = "Ts = " + str(max(popt[2], popt[3])+0.0005)[:5]
plt.text(60, 0.8, "fit result", fontdict={'size': 16, 'color': 'b'})
plt.text(60, 0.7, p_str, fontdict={'size': 16, 'color': 'b'})
plt.text(60, 0.6, q_str, fontdict={'size': 16, 'color': 'b'})

• 使用global全局变量。
• numpy 库的 piecewise() 函数写分段函数。注意这里的函数输入 x 是数组，输出也是数组。
• 从 txt 文件中读取，去空格，去换行符，转数字，切片。
• 在 curve_fit() 函数设置拟合的迭代次数。
• y_fit 列表生成器初始化列表。
• 在图片中加入文字。

$\alpha$ 信号拟合结果：

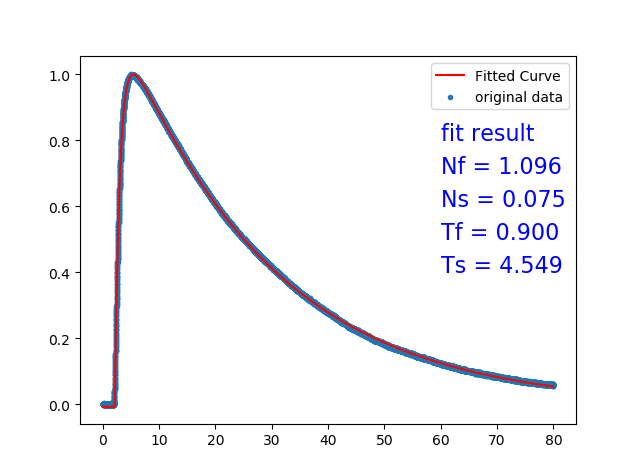
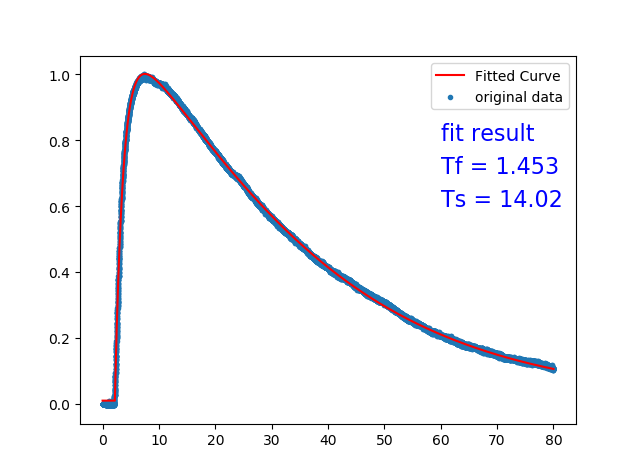
$\gamma$ 信号拟合结果：