D. Numbers on Tree（构造）【CF 1287】

传送门

思路：

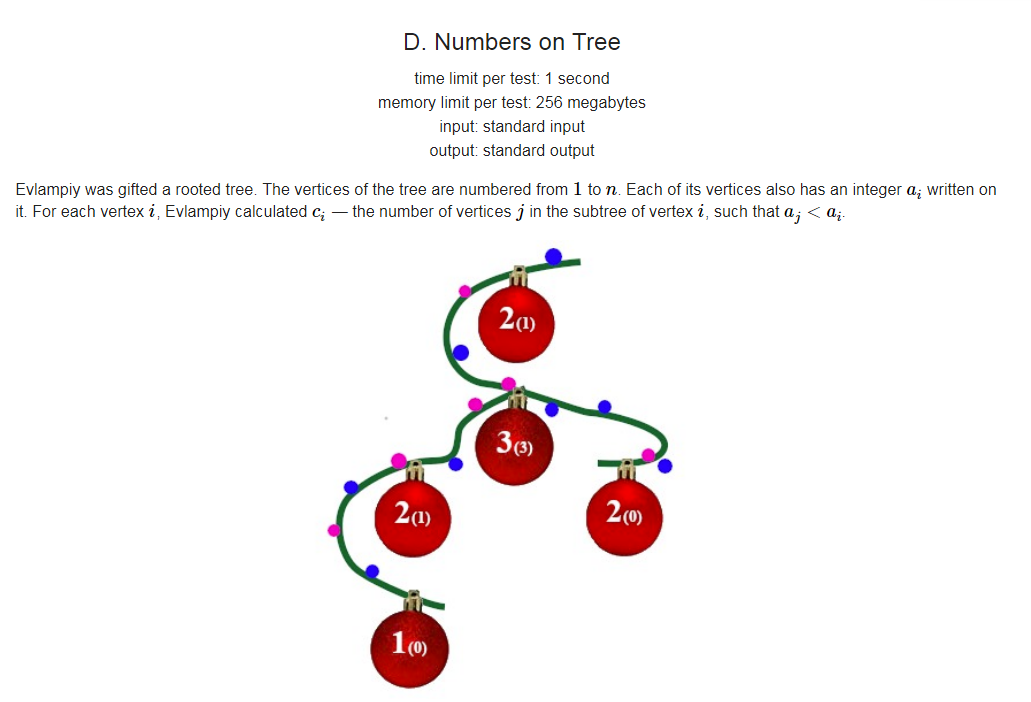
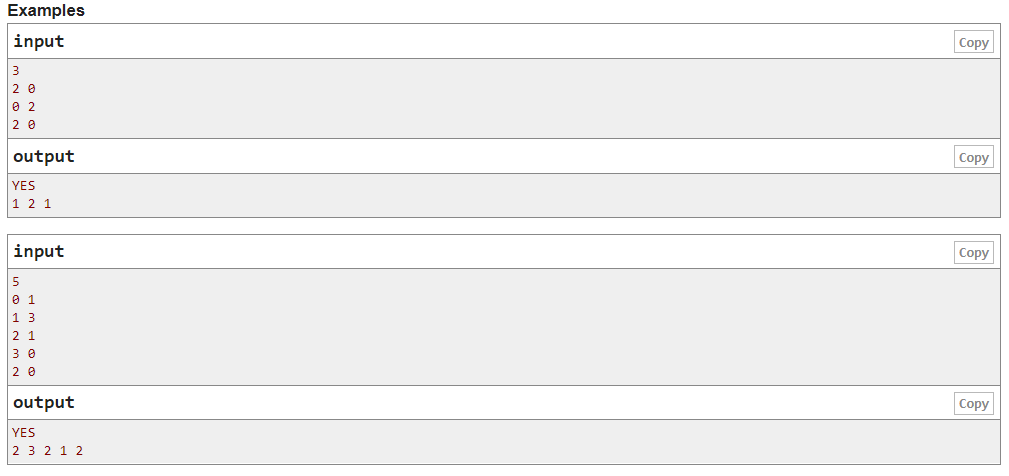
我们需要抓住唯一的重要信息点"ci"，我的做法也是在猜想和尝试中得出的，之后再验证算法的正确性。

我们在构造中发现，如果树上出现了相同的数字，则会让树的构造变得不清晰。

我们尝试用不同的数值a[1]~a[n]去构造树，我们唯一知道的信息就是"ci"，如果a[1]~a[n] = 1~n（从小到大排序），则我们容易确定root的数值id[root] = a[c[root] + 1]。为什么？因为我们有1~n这n个数字，如果我们id[root] = a[c[root] + 1]，则root下面的点，无论怎么放置这n-1个数字都满足c[root]。如果该root的左边第一个son节点的c[x] = t，则id[x]为第c[x] + 1个数字（因为id[root]被使用了）好像也行的通（红字带入也行得通），然后我按着从左开始的dfs序模拟，发现问题就解决了，这样的方法是行的通的。为什么？模拟了之后才发现，因为我们选的是不同的数字，我们如果按着从左的dfs序一个个的解决子树，只要有足够的不同数字，则该方法一定是可以构造出当前子树的信息（带入红字理解），即子树之间独立不影响。用这个构造方法之前只需要先判断下所有的ci是不是合法，即该点下面如果只有x个数字，c[now]>x就是不合法的。代码下面有个样例，模拟下就理解了。

  1 #include <iostream>
  2 #include <algorithm>
  3 #include <cstdio>
  4 #include <cstring>
  5 #include <queue>
  6 #include <string>
  7 #include <map>
  8 #include <set>
  9
 10 using namespace std;
 11
 12 const int N = 2e3 + 10;
 13 vector<int > E[N];
 14 set<int > hav;
 15 int son[N], id[N];
 16 int error;
 17
 18 int fun (int now, int pre)
 19 {
 20     int sn = 0;
 21     for(auto to : E[now]) {
 22         if(to == pre) continue;
 23         sn += fun(to, now);
 24     }
 25
 26     if(son[now] - 1 > sn) error = 1;
 27     return sn + 1;
 28 }
 29
 30 void dfs (int now, int pre)
 31 {
 32     if(son[now] > hav.size()) { error = 1; return; }
 33     else {
 34         int tot = 0;
 35         for(auto& x: hav) {
 36             ++tot;
 37             if(tot == son[now]) {
 38                 id[now] = x;
 39                // cout << x << endl;
 40                 hav.erase(x);
 41                 break;
 42             }
 43         }
 44     }
 45
 46     for(auto to : E[now]) {
 47         if(to == pre) continue;
 48         dfs(to, now);
 49         if(error) return;
 50     }
 51 }
 52
 53 void solve()
 54 {
 55     int n, root;
 56     scanf("%d", &n);
 57     for(int i = 1; i <= n; ++i) {
 58         int x, cnt;
 59         scanf("%d%d", &x, &cnt);
 60         if(x != 0) {
 61             E[i].push_back(x);
 62             E[x].push_back(i);
 63         } else root = i;
 64         son[i] = cnt + 1;
 65     }
 66
 67     for(int i = 1; i <= n; ++i) { hav.insert(i); }
 68
 69     error = 0;
 70     fun(root, 0);
 71     if(error) {
 72         printf("NO\n");
 73         return;
 74     }
 75     dfs(root, 0);
 76     if(error) { printf("NO\n"); }
 77     else {
 78         printf("YES\n");
 79         for(int i = 1; i <= n; ++i) { printf("%d ", id[i]); }
 80         printf("\n");
 81     }
 82 }
 83
 84 int main()
 85 {
 86
 87     solve();
 88
 89     return 0;
 90 }
 91 /*
 92 13
 93 0 5
 94 1 2
 95 2 0
 96 2 1
 97 4 0
 98 4 1
 99 6 0
100 6 0
101 1 1
102 9 0
103 9 2
104 11 0
105 11 0
106
107 */