Educational Codeforces Round 89 (Rated for Div. 2) D. Two Divisors (数学)

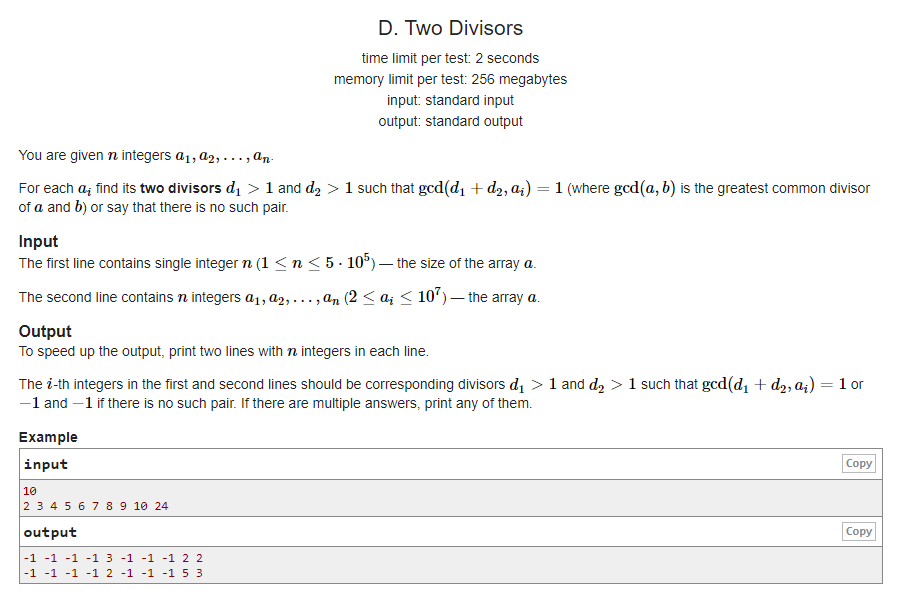
• 题意:有\(n\)组数,对于每组数,问是否能找到两个因子\(d_{1},d{2}\),使得\(gcd(d_{1}+d_{2},a_{i}=1)\),如果有,输出它们,否则输出\(-1\).

• 题解:对于这题,首先我们要推两个gcd的公式:

  ​ 1) $gcd(a,b)=gcd(a+b,b) $.

  ​ 2) 若\(gcd(a,c)=1 \ => gcd(a,bc)=gcd(a,b)\).

  这两个公式应该都很容易证明.

  因此我们推出:若\(gcd(x,y)=1\),则:\(gcd(x+y,xy)=1\).

  所以我们就可以对\(a_{i}\)质因数分解,得到:\(p_{1}^{k1},p_{2}^{k2}.....p_{n}^{kn}\).

  我们令\(d_{1}=p_{1}^{k1}\),\(d_{2}=\frac{a_{i}}{d_{1}}\)即可.

  下面给出公式的证明过程:

  

• 代码: (用到了欧拉线性筛)

  #include <iostream>
  #include <cstdio>
  #include <cstring>
  #include <cmath>
  #include <algorithm>
  #include <stack>
  #include <queue>
  #include <vector>
  #include <map>
  #include <set>
  #include <unordered_set>
  #include <unordered_map>
  #define ll long long
  #define fi first
  #define se second
  #define pb push_back
  #define me memset
  const int N = 1e7 + 10;
  const int mod = 1e9 + 7;
  const int INF = 0x3f3f3f3f;
  using namespace std;
  typedef pair<int,int> PII;
  typedef pair<ll,ll> PLL;
  
  int n;
  int prime[N];
  int cnt;
  bool st[N];
  int a[N];
  vector<int> v;
  vector<PII> ans;
  
  void get_prime(){
  	for(int i=2;i<=N;++i){
  		if(!st[i]) prime[++cnt]=i;
  		for(int j=1;j<=cnt && prime[j]<=n/i;++j){
  			st[i*prime[j]]=true;
  			if(i%prime[j]==0) break;
  		}
  	}
  }
  
  void divide(int x){
  	 int tmp=x;
       for(int i=1;i<=cnt;++i){
       	if((ll)prime[i]*(ll)prime[i]>(ll)x) break;
       	if(x%prime[i]==0){
       	  int t=1;
       	  while(x%prime[i]==0){
       		x/=prime[i];
       		t*=prime[i];
       	  }
       	  v.pb(t);
       	}
       }
       if(x>1) v.pb(x);
       if(v.size()<2) ans.pb({-1,-1});
       else ans.pb({v[0],tmp/v[0]});
       v.clear();
  }
  
  int main() {
      ios::sync_with_stdio(false);cin.tie(0);
  	cin>>n;
  	 for(int i=1;i<=n;++i){
  	 	cin>>a[i];
  	 }
  	 get_prime();
  	 for(int i=1;i<=n;++i){
  	 	divide(a[i]);
  	 }
  	 for(auto w:ans) printf("%d ",w.fi);
  	 printf("\n");
  	 for(auto w:ans) printf("%d ",w.se);
  
      return 0;
  }