EM算法——Expectation-Maximization
最大似然估计
一个栗子:假如去赌场,但是不知道能不能赚钱,你就在门口堵着出来一个人就问一个赚了还是赔了,如果问了5个人都说赚了,那么你就会认为,赚钱的概率肯定是非常大的。
已知:(1)样本服从分部的模型,(2)观测到的样本
求解:模型的参数
总的来说:极大似然估计就是用来估计模型参数的统计学方法
最大似然的数学问题(100名学生的身高问题)
样本集X = {x1, x2 ,...,xN} N = 100
概率密度:p(xi|θ)抽到男生i(的身高)的概率
θ是服从分部的参数
独立同分布:同时抽到这100个男生的概率就是他们各自概率的乘积
最大似然函数:
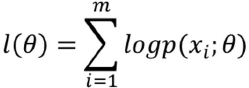 (对数是为了乘法转加法)
(对数是为了乘法转加法)
什么样的参数θ能够使得出现当前这批样本的概率最大
已知某个随机样本满足某种概率分布,但是其中具体的参数不清楚,参数估计就是通过若干次试验,观察其结果,利用结果推出参数的大概值。
问题又难了一步
现在这100个人中,不光有男生,还有女生(2个类别,2种参数)
男生和女生的身高都服从高斯分布,但是参数不同(均值,方差)
用数学的语言描述:抽取得到的每个样本都不知道是从哪个分布抽取的
求解目标:男生和女生对应的身高的高斯分布的参数是多少
加入隐变量
用Z = 0或Z = 1标记样本来自哪个分部,则Z就是隐变量
最大似然函数:
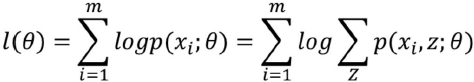
求解:在给定初始值情况下进行迭代求解
EM算法
EM算法推导:
问题:样本集{x(1),...,x(m)},包含m个独立的样本。其中每个样本i对应的类别z(i)是未知的,所以很难用最大似然求解。
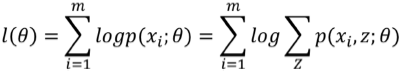
上式中,要考虑每个样本在各个分布中的情况。本来正常求偏导就可以了,但是现在log后面还有求和,这就难解了!
右式分子分母同时乘:
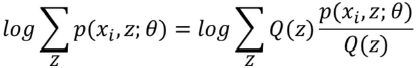
这么做就是为了凑Jensen不等式(Q(z)是Z的分布函数)
Jensen不等式
设f是定义域为实数的函数,如果对于所有的实数x。
如果对于所有的实数x,f(x)的二次导数大于等于0,那么f是凸函数。
如果f是凸函数,X是随机变量,那么:E[f(X)] > = f(E[X])
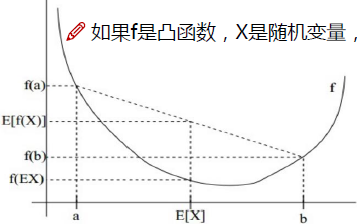
实线f是凸函数,X有0.5的概率是a,有0.5的概率是b,X的期望值就是a和b的中值了
Jensen不等式应用于凹函数时,不等号方向反向
由于:
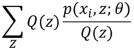 是
是 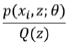 的期望
的期望
假设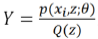 则:
则: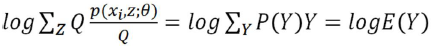
可得:
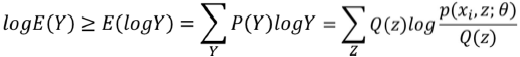
结论:
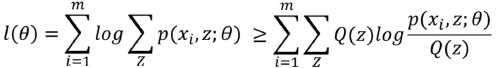
下届比较好求,所以我们要优化这个下界来使得似然函数最大
优化下届,迭代到收敛
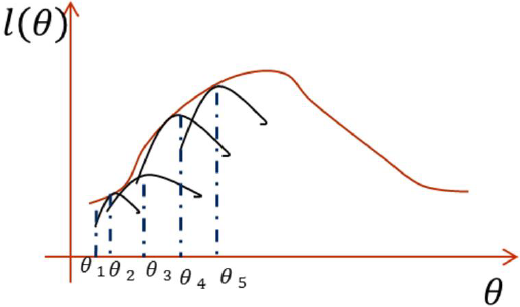
Jensen中等式成立的条件是随机变量是常数:
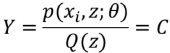
Q(z)是z的分部函数:
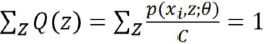
所有的分子和等于常数C(分母相同)
Q(z)求解

由上式可得C就是p(xi,z)对z求和
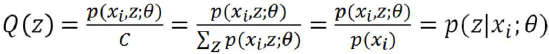
Q(z)代表第i个数据是来自zi的概率
EM算法流程
初始化分布参数Θ
E-step:根据参数Θ计算每个样本属于zi的概率(也就是Q)
M-step:根据Q,求出含有Θ的似然函数的下界并最大化它,得到新的参数Θ
不断的迭代更新
GMM(高斯混合模型)
数据可以看作是从数个Gaussian Distribution中生成出来的
GMM由K个Gaussian分布组成,每个Gaussian称为一个“Component”
类似k-means方法,求解方式跟EM一样
不断的迭代更新
EM算法——Expectation-Maximization的更多相关文章
- EM算法(Expectation Maximization Algorithm)
EM算法(Expectation Maximization Algorithm) 1. 前言 这是本人写的第一篇博客(2013年4月5日发在cnblogs上,现在迁移过来),是学习李航老师的< ...
- EM算法(Expectation Maximization)
1 极大似然估计 假设有如图1的X所示的抽取的n个学生某门课程的成绩,又知学生的成绩符合高斯分布f(x|μ,σ2),求学生的成绩最符合哪种高斯分布,即μ和σ2最优值是什么? 图1 学生成绩的分 ...
- EM算法(Expectation Maximization Algorithm)初探
1. 通过一个简单的例子直观上理解EM的核心思想 0x1: 问题背景 假设现在有两枚硬币Coin_a和Coin_b,随机抛掷后正面朝上/反面朝上的概率分别是 Coin_a:P1:-P1 Coin_b: ...
- 简单理解EM算法Expectation Maximization
1.EM算法概念 EM 算法,全称 Expectation Maximization Algorithm.期望最大算法是一种迭代算法,用于含有隐变量(Hidden Variable)的概率参数模型的最 ...
- EM 算法 Expectation Maximization
- EM(Expectation Maximization)算法
EM(Expectation Maximization)算法 参考资料: [1]. 从最大似然到EM算法浅解 [2]. 简单的EM算法例子 [3]. EM算法)The EM Algorithm(详尽 ...
- 最大期望算法 Expectation Maximization概念
在统计计算中,最大期望(EM,Expectation–Maximization)算法是在概率(probabilistic)模型中寻找参数最大似然估计的算法,其中概率模型依赖于无法观测的隐藏变量(Lat ...
- 机器学习-EM算法
最大期望算法 EM算法的正式提出来自美国数学家Arthur Dempster.Nan Laird和Donald Rubin,其在1977年发表的研究对先前出现的作为特例的EM算法进行了总结并给出了标准 ...
- 数据挖掘十大经典算法(5) 最大期望(EM)算法
在统计计算中,最大期望(EM,Expectation–Maximization)算法是在概率(probabilistic)模型中寻找参数最大似然估计的算法,其中概率模型依赖于无法观测的隐藏变量(Lat ...
- EM算法及其推广
概述 EM算法是一种迭代算法,用于含有隐变量(hidden variable)的概率模型参数的极大似然估计,或极大后验概率估计. EM算法的每次迭代由两步组成:E步,求期望(expectation): ...
随机推荐
- selenium-grid 分布式 实现同一脚本在不同pc上运行
1.使用版本:selenium 3.11.0chrome 65phantomjs 2.1.1selenium-server selenium-server-standalone-2.46.0.jar ...
- USB接口案例——多态和转型
其中,为传递和使用的匿名对象,即创建了对象,但是没有引用类和对象名来接收: 电脑类中的操作usb的成员方法中,要向下转型,毛主席讲的具体问题具体分析,不同的设备有不同的操作:
- nginx FastCGI错误Primary script unknown解决办法
在centos上成功编译安装nginx 1.4.php 5.4并成功启动nginx和php-fpm后,访问php提示"File not found.",同时在错误日志中看到: 复制 ...
- 课堂测试代码(未完全实现,部分代码有bug,仅供参考)
//信1705-3 20173507 周龙海package account; public class account { private String accountID; private Stri ...
- ubuntu16.04 无法连接wifi和校园宽带问题的解决办法
我遇到的问题是在ubuntu16.04系统下无法进行上海大学校园宽带连接或者校园wifi连接,我一个一个来解决这两个问题. 1.无法连接校园宽带的问题:输入校园账号和密码后,宽带始终连接不上.(上海大 ...
- jquery easyui datagrid 空白条处理 自适应宽高 格式化函数formmater 初始化时会报错 cannot read property 'width'||'length' of null|undefined
1---表格定义好之后右侧可能会有一个空白条 这个空白条是留给滚动条的,当表格中的一页的数据在页面中不能全显示时会自动出现滚动条,网上有很多事要改源码才可以修改这个,但是当项目中多处用到时,有的需要滚 ...
- GoldenGate实时投递数据到大数据平台(5) - Kafka
Oracle GoldenGate是Oracle公司的实时数据复制软件,支持关系型数据库和多种大数据平台.从GoldenGate 12.2开始,GoldenGate支持直接投递数据到Kafka等平台, ...
- java提供的线程池的使用
应用场景,比如你有个业务模块,非常耗时,并且还需要重复调用5次. 如果你写个for循环调用5次,调用一次3秒,那么5次就15秒,不是很友好. 这时,如果你用线程池就方便了,多线程跑,都跑完,收集到结果 ...
- sync—WaitGroup
用途:阻塞主线程的执行,直到所有的goroutine执行完成 WaitGroup总共有三个方法:Add(delta int),Done(),Wait().简单的说一下这三个方法的作用. Add:添加或 ...
- go开发工具及安装使用(Liteide)Liteide-centos6.8 安装
开发工具介绍 LiteIDE https://github.com/visualfc/liteide/blob/master/liteidex/deploy/welcome/zh_CN/readme. ...
