Beta分布深入理解

一些公式

Gamma函数

（1）

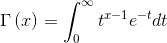
贝叶斯公式

（2）

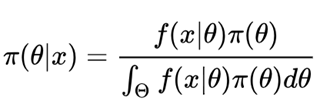
贝叶斯公式计算二项分布概率

现在有一枚未知硬币，我们想要计算抛出后出现正面的概率。我们使用贝叶斯公式计算硬币出现正面的概率。硬币出现正反率的概率和硬币两面的质量有较大关系，由于硬币未知，我们不知道是否会有人做手脚，于是在实验之前我们认为硬币出现正面的概率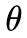服从均匀分布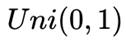，即

（3）

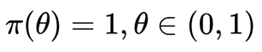
抛硬币是一个二项试验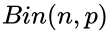，所以n次实验中出现x次正面的似然概率为

（4）

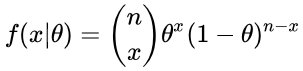
把（3）（4）式带入（2）式中，得到

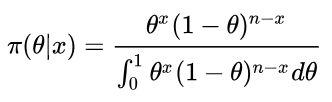
考虑到Gamma函数，进一步推算有

（5）

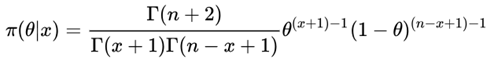
这个分布就是大名鼎鼎的Beta分布。我们记Beta函数为

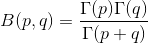
记Beta分布为

实际上，抛硬币的例子中，x为正整数，所以抛n次硬币，出现x次正面的后验概率分布为

（6）

可以看到，当a、b为整数时，Beta(a, b)与二项分布Bin(n, p)的表达式有点神似。正是因为这点神似，才让Beta分布与二项分布成为共轭分布。共轭分布我们在后续会详细讲。

Beta分布特性

我们先看看Beta分布有什么特性。

1、          Beta(1, 1)等于均匀分布。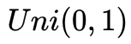

2、          作为概率的概率分布，Beta(a, b)在(0, 1)上对θ积分必定为1。

3、          Beta(a, b)同时能作为先验分布和后验分布，必定能够模拟各种概率分布情况。

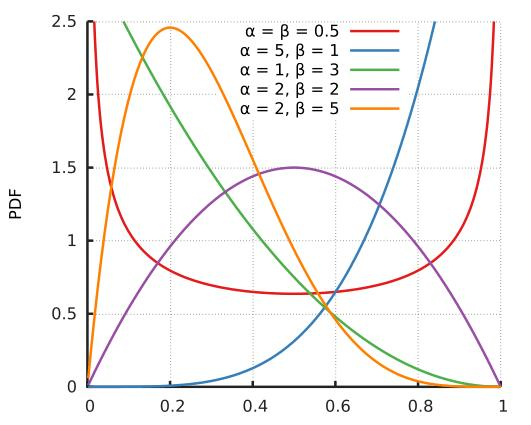
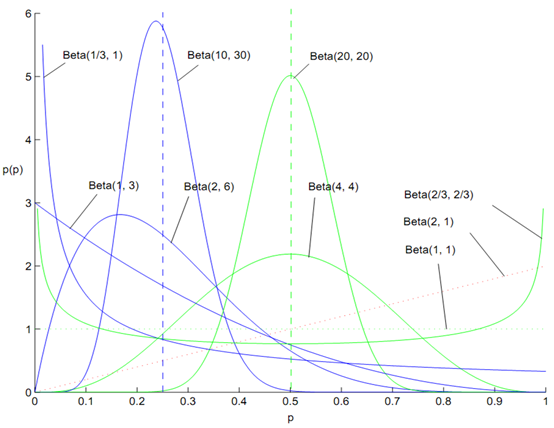
如上图，Beta分布可以模拟出以(0, 1)上任意点为峰值的曲线，这表明Beta分布可以模拟极大似然法求出的任意最大值点概率值。

Beta分布的统计例子

问题：随机变量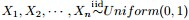，把这n个随机变量排序后得到顺序统计量，然后请问的分布是什么。

为解决这个问题，可以尝试计算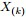落在区间[x, x+Δx]的概率。即求下述式子的值：

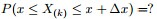
首先，把 [0,1] 区间分成三段 [0, x)，[x, x+Δx]，(x+Δx, 1]，然后考虑下简单的情形：即假设n 个数中只有1个落在了区间 [x, x+Δx]内，由于这个区间内的数X(k)是第k大的，所以[0, x)中应该有 k - 1 个数，(x+Δx, 1] 这个区间中应该有n - k 个数。如下图所示：

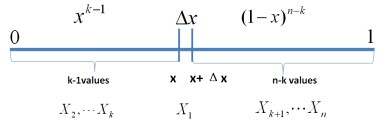
从而问题转换为下述事件E：

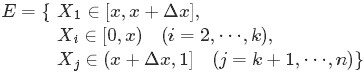
对于上述事件E，有：

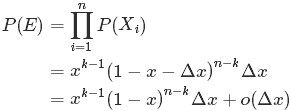
其中，o(Δx)表示Δx的高阶无穷小。显然，由于不同的排列组合，即n个数中有一个落在 [x, x+Δx]区间的有n种取法，余下n - 1个数中有k - 1个落在[0, x)的有种组合，所以和事件E等价的事件一共有个。

如果有2个数落在区间[x, x+Δx]呢？如下图所示：

类似于事件E，对于2个数落在区间[x, x+Δx]的事件E'：

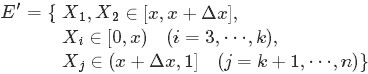
有：

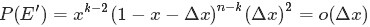
从上述的事件E、事件E'中，可以看出，只要落在[x, x+Δx]内的数字超过一个，则对应的事件的概率就是 o(Δx)。于是乎有：

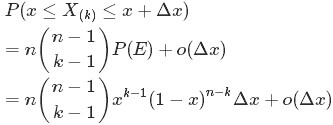
从而得到的概率密度函数为：

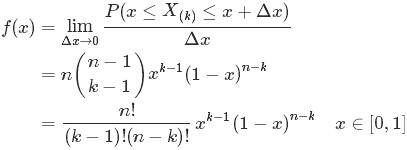
对比公式（6），可以看到上式正是a、b为整数状态下的Beta分布。

对于，我们很容易计算

共轭分布

在贝叶斯概率理论中，如果后验概率P(θ|x)和先验概率p(θ)满足同样的分布律，那么，先验分布和后验分布被叫做共轭分布，同时，先验分布叫做似然函数的共轭先验分布。

文章开头的演算中，我们已经知道使用Beta(1, 1)作为先验分布，结合贝叶斯公式和二项分布似然函数，计算出的后验分布也为Beta分布。

实际上，结合公式（2）（4）（5），我们很容易得到

Beta(a, b) + 实验数据(事件A m次，非事件A n次) ~ Beta(a + m, b + n)

参考：

https://blog.csdn.net/ccnt_2012/article/details/81113923

http://www.360doc.com/content/16/0428/10/478627_554452907.shtml#

https://www.zhihu.com/question/21134457