洛谷 P2498 [SDOI2012]拯救小云公主 解题报告

P2498 [SDOI2012]拯救小云公主

题目描述

英雄又即将踏上拯救公主的道路……

这次的拯救目标是——爱和正义的小云公主。

英雄来到\(boss\)的洞穴门口，他一下子就懵了，因为面前不只是一只\(boss\)，而是上千只\(boss\)。当英雄意识到自己还是等级1的时候，他明白这就是一个不可能完成的任务。

但他不死心，他在想，能不能避开\(boss\)去拯救公主呢，嘻嘻。

\(Boss\)的洞穴可以看成一个矩形，英雄在左下角\((1,1)\)，公主在右上角(row,line)\(。英雄为了避开\)boss\(，当然是离\)boss\(距离越远越好了，所以英雄决定找一条路径使到距离\)boss$的最短距离最远。

Ps:英雄走的方向是任意的。

你可以帮帮他吗？

当英雄找到了美丽漂亮的小云公主，立刻就被\(boss\)包围了！！！英雄缓闭双眼，举手轻挥，白光一闪后使用了回城卷轴，回到了城堡，但只有小云公主回去了……因为英雄忘了进入回城的法阵了。

输入输出格式

输入格式：

第一行，输入三个整数，\(n\)表示\(boss\)的数目，\(row\)，\(line\)表示矩形的大小；

接下来\(n\)行，每行分别两个整数表示\(boss\)的位置坐标。

输出格式：

输出一个小数，表示英雄的路径离\(boss\)的最远距离，精确到小数点后两位。

---

感觉这题好神，没见过模型的话。

70pts：

二分答案最远距离，并查集维护boss所在圆是否连通。

复杂度：\(O(log?N^2)\)

期望得分：70 实际得分：70~100

100pts：

(1) 最小生成树

这样去看，英雄通过这个平面图，实际上只有两种类型。

一是穿过个两个boss之间的地方，这时我们走两个boss之间最中间的地方是最划算的。

二是穿过边界和boss之间的地方，这时我们贴着边界走是最划算的。

我们有很多个这样的地方可以走，走哪些我们可以确定既可以穿过去所有的boss又能使它距离我们最远呢？

如果我们把这些点（包括边界抽象出来的点）连成一条链

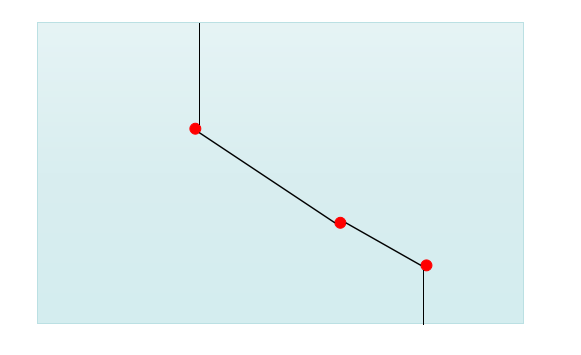
我们可以选择一个最优的方案，从中间穿过去

然而仔细想想，如果通过了另外的两点比最大距离还小的点，那不就废了吗？

换一种角度理解好了

按照\(kruskal\)的方法，我们一个一个从小到大加边

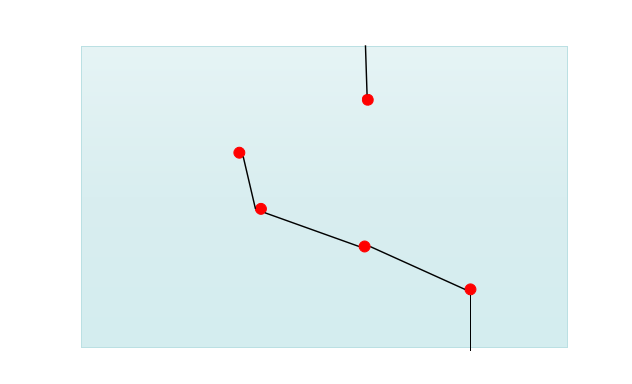
当上面的边和下面的边所代表的虚点（实际上有四种情况）连通时，我们就不得不对这条链（实际形态应该是树的连接两个虚点的链）上的某一边做出选择了，这时候我们选择之中最大的走，也不会遇到更小的两点距离了

注意如果是boss和Boss之间的边权要除2（走中间）

然而这个题只可以用prim算法（稠密图）

复杂度：\(O(N^2)\)

期望得分：100 实际得分：100

(2) SPFA

实质上SPFA也只是求得了这条在最小生成树上的最大边的权值。

我们跑0点到n+1点（两个虚点）之间的每条路径上最长的边其中的最小值

注意松弛目的是最小值，但松弛时是从前面的边的最小值和当前边选出一个最大的

复杂度：\(O(N^2)\) (建图)

期望得分：100 实际得分：100

贴一下SPFA的代码吧

#include <cstdio>
#include <cmath>
#include <queue>
double min(double x,double y){return x<y?x:y;}
double max(double x,double y){return x>y?x:y;}
const int N=3050;
double g[N][N],dis[N],x[N],y[N],n,m;
int num,used[N];
double get(double x1,double y1,double x2,double y2)
{
    return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2))/2;
}
void init()
{
    scanf("%d%lf%lf",&num,&n,&m);
    for(int i=1;i<=num;i++)
        scanf("%lf%lf",x+i,y+i);
    for(int i=1;i<=num;i++)
        for(int j=i+1;j<=num;j++)
            g[i][j]=g[j][i]=get(x[i],y[i],x[j],y[j]);
    for(int i=1;i<=num;i++)
    {
        g[0][i]=g[i][0]=min(x[i]-1,m-y[i]);
        g[i][num+1]=g[num+1][i]=min((n-x[i]),y[i]-1);
    }
    g[0][num+1]=g[num+1][0]=1e233;
    dis[0]=0;
    for(int i=1;i<=num+1;i++)
        dis[i]=1e233;
}
void spfa()
{
    std::queue <int > q;
    q.push(0);
    while(!q.empty())
    {
        int u=q.front();
        q.pop();used[u]=0;
        for(int i=1;i<=num+1;i++)
        {
            if(i==u) continue;
            if(dis[i]>max(dis[u],g[u][i]))
            {
                dis[i]=max(dis[u],g[u][i]);
                if(!used[i])
                {
                    used[i]=1;
                    q.push(i);
                }
            }
        }
    }
}
int main()
{
    init();
    spfa();
    printf("%.2lf",dis[num+1]);
    return 0;
}

---

2018.7.12