关于后缀数组的倍增算法和height数组

自己看着大牛的论文学了一下后缀数组，看了好久好久，想了好久好久才懂了一点点皮毛TAT

然后就去刷传说中的后缀数组神题，poj3693是进化版的，需要那个相同情况下字典序最小，搞这个搞了超久的说。

先简单说一下后缀数组。首先有几个重要的数组：

·SA数组（后缀数组）：保存所有后缀排序后从小到大的序列。[即SA[i]=j表示排名第i的后缀编号为j]
        ·rank数组（名次数组）：记录后缀的名次。[即rank[i]=j表示编号为i的后缀排名第j]

用倍增算法可以在O(nlogn)时间内得出这两个数组。

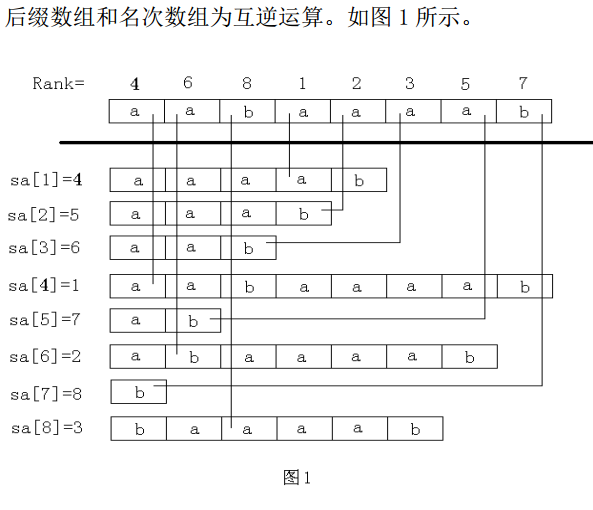
具体过程如下：

即每次长度增加一倍，直接用前面算出的排名作为关键字，问题转化为给有两个关键字的序列排序，这里可以用基数排序，每次排序时间为n，一共进行了logn次，所以总共时间复杂度为O(nlogn)。要注意如果一个字符串包含另一个字符串，长度小的较小，那就是说如果没有第二关键字，把第二关键字默认为0即可。具体如下：

数组y保存的是对第二关键字排序的结果

数组wr保存的是对第二关键字排序后的rank值

ln为当前子串的长度

rank值为排名，在这里即为关键字的值

排序时如果两个关键字相同即默认位置前的较小，那么我们先按照第二关键字排序，再按照第一关键字排序，最后排出来的就是第一第二关键字合并的结果（基数排序的方法）

    下一步是计算新的rank值。这里要注意的是，可能有多个字符串的rank值是相同的，所以必须比较两个字符串是否完全相同，wr数组的值已经没有必要保存，为了节省空间，这里用wr数组保存rank值。

一直做到所有后缀的排名不同结束，时间复杂度为O(nlogn)。

后缀数组的大部分应用都跟一个很重要的height数组有关。

height数组定义：定义height[i]=suffix(sa[i-1])和suffix(sa[i])的最长公共前缀，也就是排名相邻的两个后缀的最长公共前缀。

对于j和k，不妨设rank[j]<rank[k],则有以下性质：

　　　　suffix(j)和suffix(k)的最长公共前缀为:

　　　　height[rank[j]+1], height[rank[j]+2], height[rank[j]+3], …, height[rank[k]]中的最小值。

h数组有以下性质： h[i]≥h[i-1]-1

证明：

　　　　设suffix(k)是排在suffix(i-1)前一名的后缀，则它们的最长公共前缀是h[i-1]。那么suffix(k+1)将排在suffix(i)的前面（这里要求h[i-1]>1，如果h[i-1]≤1，原式显然成立）并且suffix(k+1)和suffix(i)的最长公共前缀是h[i-1]-1，所以suffix(i)和在它前一名的后缀的最长公共前缀至少是h[i-1]-1。因此得证。（如图）

　　按照h[1],h[2],……,h[n]的顺序计算,并利用h数组的性质，时间复杂度可以降为O(n)。

　  实现的时候其实没有必要保存h数组，只须按照h[1],h[2],……,h[n]的顺序计算即可。

标程如下：

 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<iostream>
 #define Maxn 11000
 using namespace std;
 
 int sa[Maxn],rank[Maxn],y[Maxn],Rsort[Maxn];
 int wr[Maxn],n,a[Maxn],height[Maxn];
 
 //cmp 第一关键字且第二关键字相同
 bool cmp(int k1,int k2,int ln){return wr[k1]==wr[k2] && wr[k1+ln]==wr[k2+ln];}
 int mymax(int x,int q) {return x>q?x:q;}
 
 void get_sa(int m) //构建SA后缀数组
 {
   int i,k,p,ln;
 
   memcpy(rank,a,sizeof(rank));
   //a数组:原字符串，rank名次数组
 
   for (i=;i<=m;i++) Rsort[i]=;
   for (i=;i<=n;i++) Rsort[rank[i]]++;
   for (i=;i<=m;i++) Rsort[i]+=Rsort[i-];
   for (i=n;i>=;i--) sa[Rsort[rank[i]]--]=i;
   //以上四句为基数排序，不懂的看flash
 
   ln=; p=;
   // ln为当前子串的长度,p表示有多少不相同的子串
   while (p<n)
   {
       for (k=,i=n-ln+;i<=n;i++) y[++k]=i;
       for (i=;i<=n;i++) if (sa[i]>ln) y[++k]=sa[i]-ln;
       for (i=;i<=n;i++) wr[i]=rank[y[i]];//在这里rank表示一个值
       //数组y保存的是对第二关键字排序的结果(2-sa)。
       //数组wr保存的是对第二关键字排序后的rank值(rank即第一关键字)
       //wr[i]->第二关键字排名为i的第一关键字的值
       //以下为对第一关键字排序
       for (i=;i<=m;i++) Rsort[i]=;
       for (i=;i<=n;i++) Rsort[wr[i]]++;
       for (i=;i<=m;i++) Rsort[i]+=Rsort[i-];
       for (i=n;i>=;i--) sa[Rsort[wr[i]]--]=y[i];
 
       memcpy(wr,rank,sizeof(wr));
       p=; rank[sa[]]=;
       for (i=;i<=n;i++)
       {
          if (!cmp(sa[i],sa[i-],ln)) p++;
          rank[sa[i]]=p;
       }
       //得到新的rank数组
       m=p; ln*=;//m个rank ln长度
   }
   a[]=; sa[]=;
 }
 
 void get_he()
 {
   int i,j,kk=;
   //height[i]表示排名为i的子串和比起前一位排名的子串的最长公共前缀
   for (i=;i<=n;i++) //目前求的是位置为i的子串的height值
   {
      j=sa[rank[i]-];
      if (kk) kk--;
 
      while (a[j+kk]==a[i+kk]) kk++;
      height[rank[i]]=kk;
   }
 }
 
 int main()
 {
     int i,m=-;
     char c;
     n=;
     while()
     {
         scanf("%c",&c);
         if(c=='\n') break;
         a[++n]=c-'a';
     }
     for (i=;i<=n;i++)
      m=mymax(m,a[i]);
     get_sa(m+);
     for(i=;i<=n;i++)
      printf("%d ",sa[i]);
 
 }

后缀数组

---

做poj3415的时候感觉上面那个代码有点小瑕疵诶~

还有一个地方：

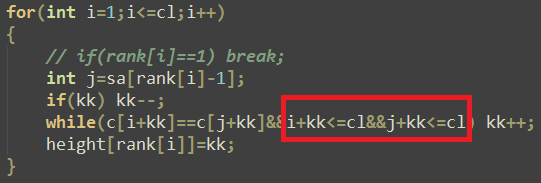
可以注意一下~~