【刷题笔记】LeetCode 222. Count Complete Tree Nodes

题意

给一棵 complete binary tree，数数看一共有多少个结点。做题链接

直观做法：递归

var countNodes = function(root) {
    if(root===null) return 0;
    return 1+countNodes(root.left)+countNodes(root.right);
};

老实说，一道难度为 medium 的题目，这么几秒钟的时间就做出来，我心中有一种不真实感。

所以，我看了一下 discuss 区其他人的解法，看是不是我自己想的不够深入。

结果发现，我这个做法没错，就是时间复杂度不够优化，如果这道题要真正成为一道难度为medium的题目，需要限制时间复杂度。

下面是一种据说是 O(log(n)^2) 的解法，很聪明，根据不同树结构选择计算左树结点数或右树节点数，可以省去访问大部分结点的时间。

优化做法：计算树高，观察树结构

var countNodes = function(root) {
    let h = height(root);
    return h === 0 ? 0 :
            height(root.right)=== h-1 ? (1 << (h-1)) + countNodes(root.right) :

                                        (1 << (h-2)) + countNodes(root.left) ;
};
function height(root){
    return root === null? 0 : 1+height(root.left);
}

首先，height 函数，没啥好说的，跟普通的计算树高度函数不同点在于，充分利用了 complete binary tree 的特点，更加省事。

其次，要理解根据 root 的高度 和 右子树高度的不同情况的选择。

情况一：

height(root) === 0

这个情况没啥好说的，就是边界情况，啥结点都没有，返回0；

情况二：

height(root.right) === h-1

这个情况就是下面图这种情况，右子树至少最左边有一个结点（这个结点把右子树的高度撑到 h-1）：

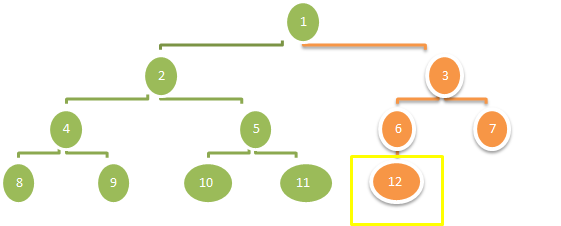
这种情况下，左子树是完整的，它的节点数是  2^(h-1)-1 ，加上根结点，等于  2^(h-1) ，也就是  1 << (h-1) （图中绿色结点总数）。

情况三：

height(root.right) === h-2

这种情况就是右子树最后一层没有任何结点，左子树至少最后一层最左边有一个结点：

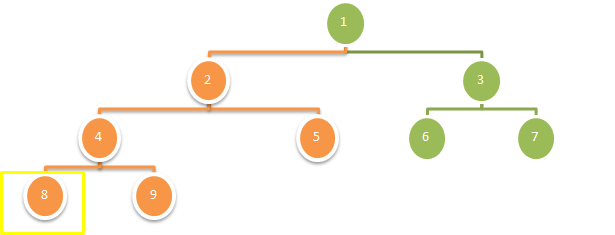
这种情况下，右子树是完整的，它的节点数是  2^(h-2)-1 ，加上根结点，等于  2^(h-2) ，也就是  1<<(h-2) （图中绿色结点总数）。

再次优化：用遍历取代递归

直接遍历所有的节点，可以省下反复计算 height 的不必要的时间。

因为很明显，子树的高度 跟 父树的高度 息息相关。如果通过递归，下一次还得重新计算高度值；而用遍历，直接  h--;  就得到子树高度值。（当然你也可以在递归函数中把高度当成参数传递进去，但是不够简洁，没必要）

var countNodes = function(root) {
    let h = height(root), nodes = 0;
    while(root!==null){
        if(height(root.right)===h-1){
            nodes += 1 << (h-1);
            root = root.right;
        }
        else{
            nodes += 1 << (h-2);
            root = root.left;
        }
        h--;
    }
    return nodes;
};
function height(root){
    return root===null? 0 : 1+height(root.left);
}

第一种简单方法的优化

最开始我用了一种最简单的方法：

var countNodes = function(root) {
    if(root===null) return 0;
    return 1+countNodes(root.left)+countNodes(root.right);
};

在 LeetCode 的 discuss 区看到 一种优化方法：

var countNodes = function(root) {
    if(root===null) return 0;
    let left = root.left, right = root.right, height = 1;
    while(right !== null){
        left = left.left;
        right = right.right;
        height++;
    }
    if(left === null) return (1 << height)-1;
    return 1 + countNodes(root.left) + countNodes(root.right);
};

这种方法其实也是利用了 Complete Binary Tree 的特点，如果一棵树是完整的（就是它所有树叶都处于同一层），那么在 右子树 为  null  之前， left = left.left; right = right.right; 最左最右两个分枝同时向下延伸，最后一定同时抵达树叶。

这种方法的优化之处在于，当遇到的子树的所有树叶都位于同一层时，它会直接返回该子树的结点数。像下面这样的树，当遇到结点 3， 5， 8 时，不会再调用函数递归，而是直接计算出整颗子树的结点数  (1 << height) - 1 。

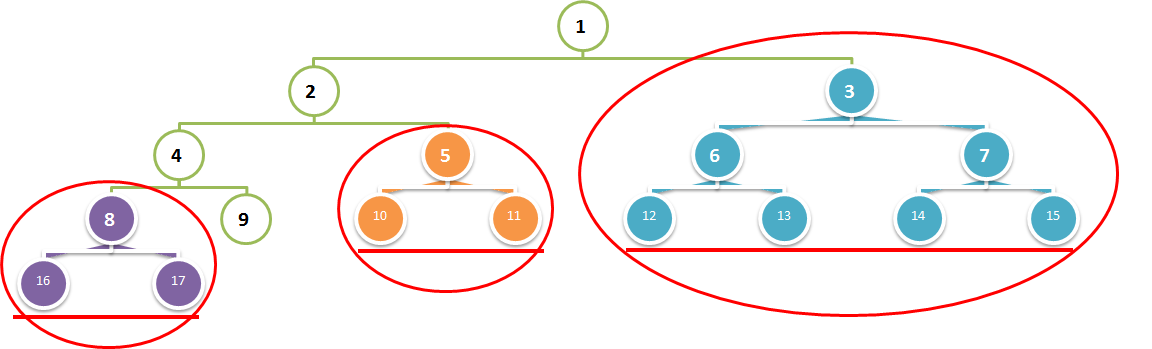
总结

要了解数据结构的特点，并且充分利用这些特点来省事。

PS：上面全部代码为 JavaScript