1x1卷积核作用

1. 实现跨通道的交互和信息整合

对于某个卷积层，无论输入图像有多少个通道，输出图像通道数总是等于卷积核数量！

对多通道图像做1x1卷积，其实就是将输入图像于每个通道乘以卷积系数后加在一起，即相当于把原图像中本来各个独立的通道“联通”在了一起。

2. 进行卷积核通道数的降维和升维

进行降维和升维引起人们重视的（可能）是在GoogleNet里。对于每一个inception模块（如下图），原始模块是左图，右图中是加入了1x1卷积核进行降维的。

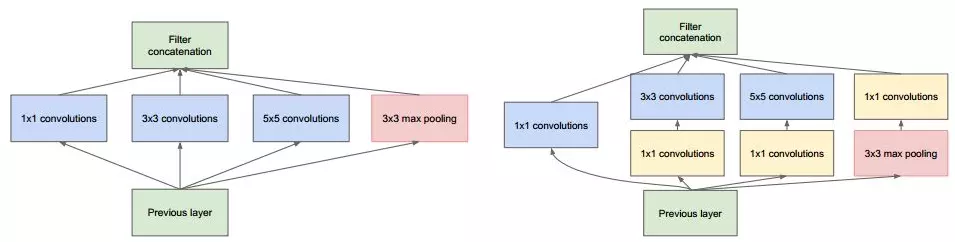
虽然左图中的卷积核都比较小，但是当输入和输出的通道数很大时，乘起来也会使得卷积核参数变很大，而右图加入1x1卷积后可以降低输入的通道数，卷积核参数、运算复杂度也就降下来了。