关于L'Hopital法则

1.首先需要使用 罗尔定理

函数f(x)在闭区间[a,b]连续在开区间（a,b)可微，如果f(a)=f(b)，那么至少存在一点c使函数导数f'(c)=0

注意需要再(a,b)可微，如果函数有角点，断点，尖点，那么就不一定存在c，使f'(c)=0成立，（当然也有可能成立，如果有其他可做水平切线的点0

涉及的图片参考http://www.cnblogs.com/wdfrog/p/5956840.html

注意f(a)=f(b)=0 等于0不是必需，因为只要f(a)=f(b)那么就可通过上下平移得到f(a)=0

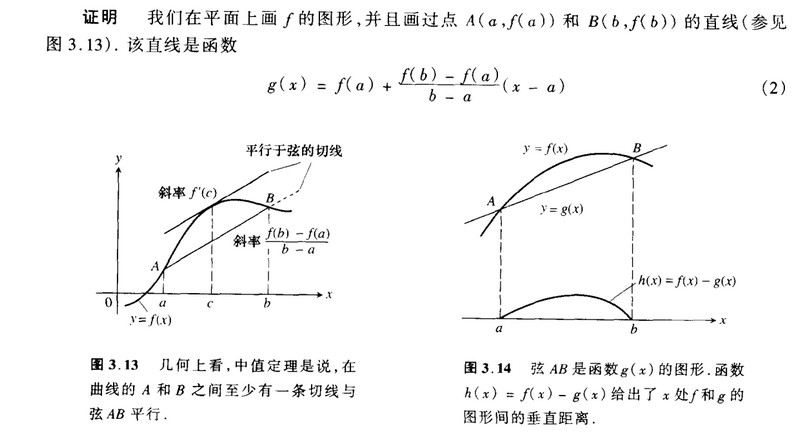
2.根据罗尔定理，可以导出拉格朗日中值定理即

符合上面条件并且 f(a)<>f(b)时

至少能找到一点使 f'(c)=[f(b)-f(a)] / (b-a)

柯西中值定理

条件：设函数 满足
⑴在闭区间 上连续；
⑵在开区间 内可导；
⑶对任意 x属于(a,b)，g'(x)<>0  ，
那么在 内至少有一点 ，使得[f(b)-f(a)]/[g(b)-g(a)]=f'(ξ)/g'(ξ)成立
与拉氏定理的联系
在柯西中值定理中，若取g(x)=x时，则其结论形式和拉格朗日中值定理的结论形式相同。
因此，拉格朗日中值定理为柯西中值定理的一个特例；反之，柯西中值定理可看作是拉格朗日中值定理的推广。

证明

可构造辅助函数F(x)=[g(b)-g(a)]f(x)-[f(b)-f(a)]g(x);

有F(a)=F(b);由罗尔定理，有

存在ξ∈(a,b),使得F'(ξ)=0,即

[g(b)-g(a)]f'(x)-[f(b)-f(a)]g'(x)=0;

又

  

，有

 

上面的构造的函数F(x)满足F(a)=F(b)所以求导后，在[a,b]区间里存在一点ξ，使F'(ξ)=0

 

洛必达法则与证明

注意在[x0,x]区间上，存在一点c使柯西中值定理成立，又因为f(x0)=g(x0)=0 所以两边同时取lim_(x->x0+)时等式成立

由于 lim_(x->x0) f'(x)/g'(x) 本质上还是lim_(x->x0) f(x)/g(x) （--都是关于x的有真函数之比 ） 所以强形式的洛必达法则可以迭代使用（连续使用）

上面的条件一表示当x->a时f(x),F(x)都趋于0,对应下面的辅助函数f1(a)=F1(a)=0

不支持迭代使用的洛必达法则

注意 lim_(x->a) f'(x)/g'(x) <> f'(x)/g'(x) 所以该形式是不支持迭代使用的,当碰到第一次求导后还是0/0的情况就要使用加强形式的定理