EM(Expectation Maximization )

概括

看李航老师的《统计学习方法》知道，EM是一个对于有隐含随机变量的概率模型的参数的估计方法，它是一种无监督的算法。

只是有些重要的点并没有给出， 比如没有三硬币例子中直接给出的 u(z), π ，p, q的公式，并没有推到过程， 让人使用起来有些迷惑。

通过浏览了一些网上一些优秀的文章，本文把三硬币问题和EM算法的细节重新阐述一下，以补充李航老师书中的内容，从而加深理解 。

三硬币问题

假设有3枚硬币，分别记作A,B,C。这些硬币正面出现的概率分别为  ,  和  。进行如下投掷实验：先投掷硬币A，根据其结果选出硬币B或者硬币C，正面选硬币B，反面选硬币C；然后投掷选出的硬币，投掷硬币的结果，出现正面记作1，出现反面记作0；独立地重复n次实验 （这里n=10)。观测结果如下：

1,1,0,1,0,0,1,0,1,1

假设只能观测到投掷硬币的结果，不能观测投掷硬币的过程。问如何估计三硬币正面出现的概率, 即三硬币模型的参数。

EM 算法 的数学推导

没办法，想要深刻理解EM 算法的原理， 必须理解下面的数学： 静下心来， 是可以看懂的。

如《统计学习方法》所述， 三硬币问题的观测数据不是完全数据， 因为无法看到A的数据，A在本问题里的隐藏事件，按惯例记作 z, 观测数据（结果）记作 y.

观测数据为 y1,y2,...,y10, (取值：1或0， 代表最终看到的硬币（B或C）的正反面)， 隐藏数据为z1,z2,...,z10(取值：1或0， 代表A硬币的正反面) .

如果用最大似然的方法估计y概率模型参数，似然函数 是 每个样本的联合概率， 即：

L (y:θ,π) = p(y1,y2,...,y10 :θ,π)

其中， z 和模型参数解释如下 ：

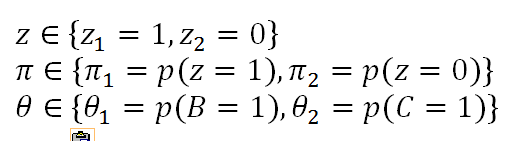
对于每一y样本的概率p(y_i) 是 A或B投掷结果为y_i 关于z 的数学期望， 表示如下：

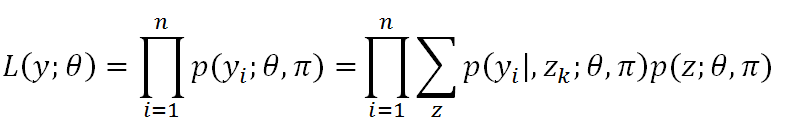
对于上面的三硬币式样结果， 展开式为：

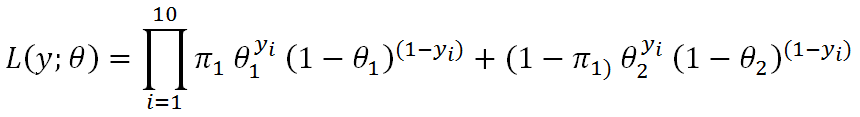
按照惯例， 对L (y:θ,π)求对数， 将乘法转换成加法。

上式展开后，无法通过求最大值（也就是最大似然）从而获取θ和π的值：所谓最大似然估计就是当似然函数达到最大值时的参数。

可是，因为在上式中，θ和π并不不互相独立 （有乘法关系）， 无法通过使偏导为0从而求得θ或π （比如将θ偏导函数置0后，θ依然依赖π）。

下面过程是利用Jensen不等式进行变形 。 引入R(Z;θ，π）， 它是z 的一个概率分布， 模型参数等同于L (y:θ,π) ，R(Z;θ，π）> 0 。将它带入 l(y:θ,π) 如下：

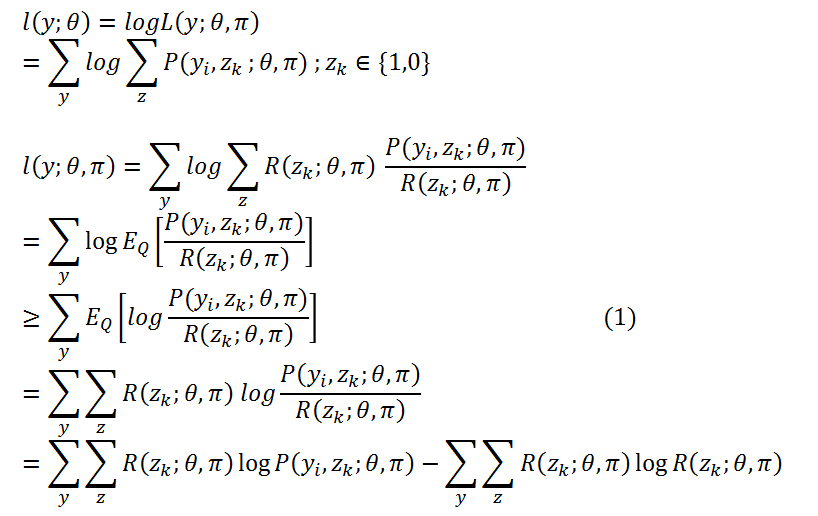
EM 算法 的步骤

第一步：选择参数的初始值

选择参数的初始值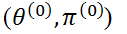 

E 步 ： 求Expectation 

M 步： Maximization

第四步：反复迭代，直到收敛

三硬币模型中的 EM

参数和z值：

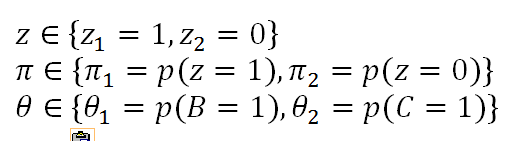
下面的步骤是推导出李航老师书中给出的公式。

E 步 ：

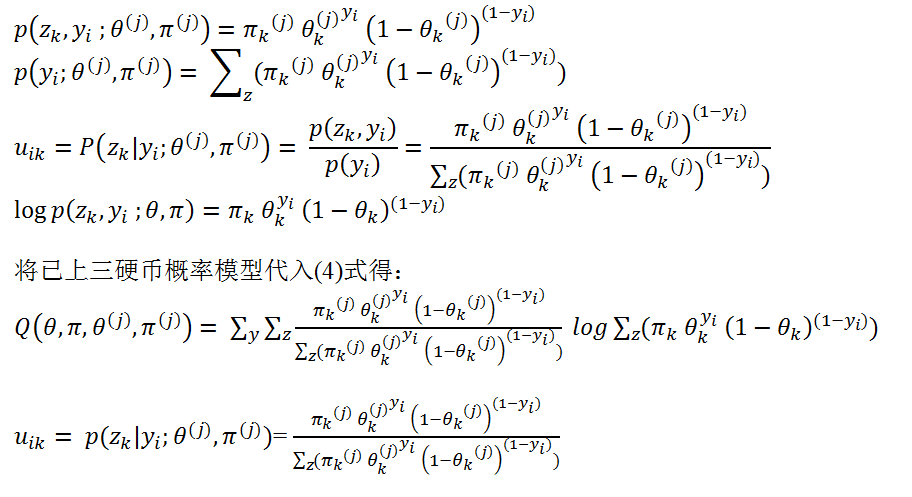
M 步：

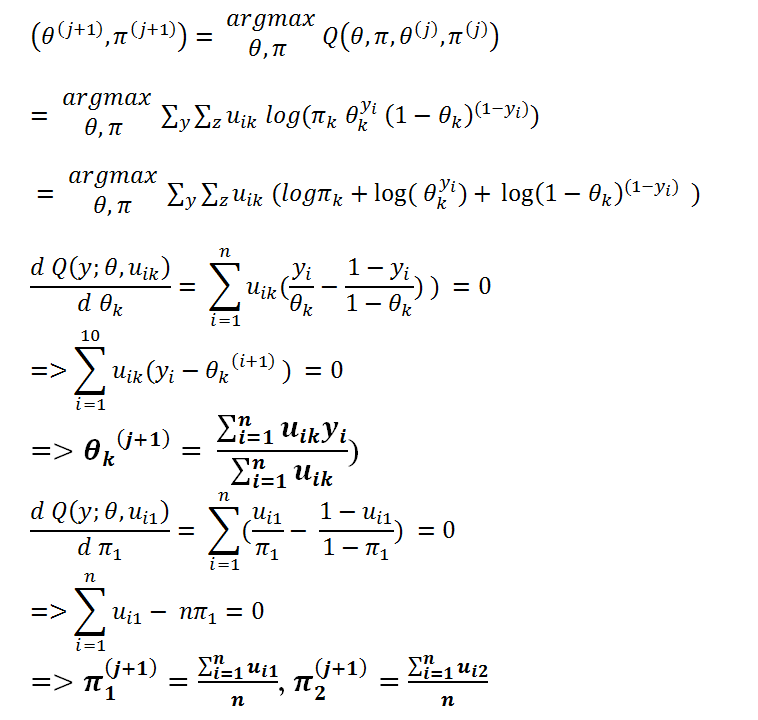
高斯混合模型中的EM

下图三个二元高斯分布组成的高斯混合模型的有lable观察值。我们可以用最大似然的方法求得三个高斯分布的各自的参数（υ_k，Σ_k），每一个分布根据（υ_k，Σ_k）都有一个椭圆型的范围， 因此就已对平面上的其他测试点进行分类。

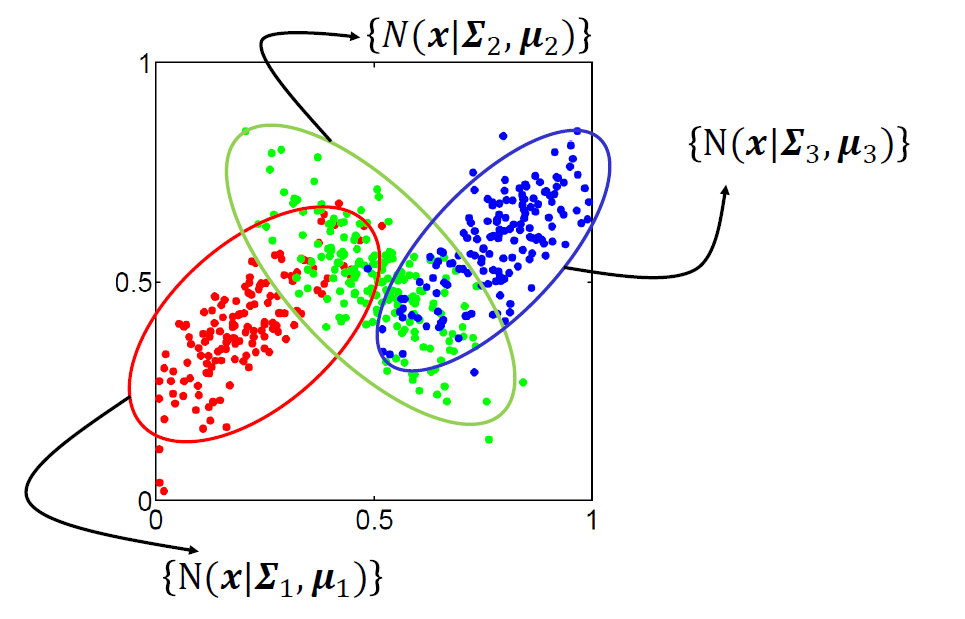
但是对于下面这种这种没有label 的观测数据怎么求得三个高斯分布的各自的参数（υ_k，Σ_k） ？ 答案是 EM 。

 

参数和z值 :

E 步 ：

M 步 ：

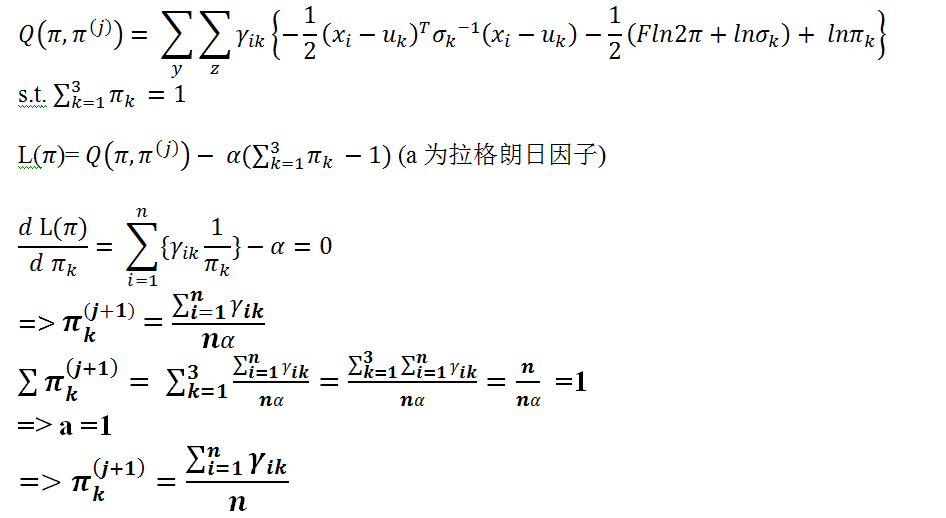
Jensen不等式：

如果f是凸函数，X是随机变量，那么：

当f为凹函数是：E[f(X)]>=f(E[X])

当f为凸函数是：E[f(X)]>=f(E[X])

特别地，如果f是严格凸(凹)函数，当且仅当X是常量时，上式取等号。

如果用图表示会很清晰：

下面证明为什么当 X常量时，二式相等。

E[f(X)] = ΣP(X)f(X) ; f(E[X]) = f(ΣP(X)X)

X常量， 则

E[f(X)] = ΣP(X)f(c) = f(c) ΣP(X) = f(c); f(E[X]) = f(ΣP(X)c) =f(cΣP(X)) = f(c)

故E[f(X)] =f(E[X])= f(c)

参考

《统计学习方法》 李航

https://ibug.doc.ic.ac.uk/media/uploads/documents/expectation_maximization-1.pdf

https://zhuanlan.zhihu.com/p/32049842

https://www.zhihu.com/question/27976634