[jzoj]3506.【NOIP2013模拟11.4A组】善良的精灵(fairy)（深度优先生成树）

Link

　　https://jzoj.net/senior/#main/show/3506

Description

　　从前有一个善良的精灵。
　　一天，一个年轻人B找到她并请他预言他的未来。这个精灵透过他的水晶球看到这个年轻人将要遇见一个非常美丽的公主并要娶她。。精灵在一张纸上画了N个点并用一些线段将他们连起来，每条线段两端连着不同的点。画完了之后，精灵让年轻人去除一条线段。然后精灵尝试将每个点用红色或者蓝色进行染色，同时使得那里没有一条线段的两端是相同的颜色。如果精灵能够成功染色，这个预言就能成真。
　　年轻人想要遇见那位公主，因此他请求你去帮助他，找到所有的删除之后能对图进行成功染色的线段。

Solution

0~99分

　　显然爆搜。

100分

　　题目大意就是“给你一个无向图，让你删去一条边，使得原图无奇环”

　　既然考虑到环的奇偶性，自然就得考虑到其个数。按照惯例，绘制一个深度优先生成树（DFS树）

　　怎么绘制呢？

　　选择一个点为根，按照DFS的顺序，连出一棵树。当一个点连向一个深度小与它的点，显然，就构成了一个环。

　　我们称这条边为返祖边，这个环的大小就是两点深度差+1。

　　然后在树上弄一个类似差分约束的思路，来求出当前边被多少个奇数，偶数环所包括。

　　

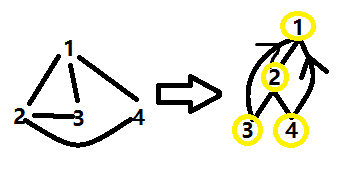
　　对于一条边

　　（1）全图无环或者只有一个偶环，当前边可以删　　

　　（2）如果不符合（1），可以删当前边，仅当当前边被这个图所有奇数环覆盖，且不被一个偶数环包括。

　　引理1易证

　　引理2：如果奇数和偶数环在一起，删完后一定不满足。如果不包括所有奇数环，那么在不被当前边包括的奇数环就不满足。

Code

{$inline on}
var
        n,m,i,x,y,tot,tot1,papa:longint;
        w:array[..] of longint;
        dis:array[..] of boolean;
        data:array[..] of longint;
        pre,tov,last:array[..] of longint;
        pre1,tov1,cos1,last1:array[..] of longint;
        ji,ou,numj,numo:array[..] of longint;
procedure insert(x,y:longint);  inline;
begin
        inc(tot);
        tov[tot]:=y;
        pre[tot]:=last[x];
        last[x]:=tot;
end;

procedure insert1(x,y,z:longint); inline;
begin
        inc(tot1);
        tov1[tot1]:=y;
        cos1[tot1]:=z;
        pre1[tot1]:=last1[x];
        last1[x]:=tot1;
end;

procedure dg(x,q,shen:longint); inline;
var
        k:longint;
begin
        dis[x]:=true;
        w[x]:=shen;

        k:=last[x];

        while k<> do
        begin
                if tov[k]<>q then
                begin
                        if not dis[tov[k]] then
                        begin
                                insert1(x,tov[k],(k+) shr );

                                dg(tov[k],x,shen+);
                        end
                        else
                        if w[tov[k]]<w[x] then
                        begin
                                if odd(w[tov[k]]-w[x]+) then
                                begin
                                        inc(ji[x]);
                                        dec(ji[tov[k]]);

                                        numj[(k+) shr ]:=;

                                        inc(papa);
                                end
                                else
                                begin
                                        inc(ou[x]);
                                        dec(ou[tov[k]]);

                                        numo[(k+) shr ]:=;
                                end;
                        end;
                end;

                k:=pre[k];
        end;
end;

procedure find(x:longint); inline;
var
        k:longint;
begin
        k:=last1[x];

        while k<> do
        begin
                find(tov1[k]);

                numj[cos1[k]]:=ji[tov1[k]];
                numo[cos1[k]]:=ou[tov1[k]];

                inc(ji[x],numj[cos1[k]]);
                inc(ou[x],numo[cos1[k]]);

                k:=pre1[k];
        end;
end;
begin
        assign(input,'fairy.in');reset(input);
        assign(output,'fairy.out');rewrite(output);

        readln(n,m);

        for i:= to m do
        begin
                readln(x,y);

                insert(x,y);
                insert(y,x);
        end;

        for i:= to n do
                if not dis[i] then
                begin
                        dg(i,,);

                        find(i);
                end;

        for i:= to m do
                if ((numj[i]=papa) and (numo[i]=)) or (papa=) then
                begin
                        inc(data[]);

                        data[data[]]:=i;
                end;

        writeln(data[]);

        for i:= to data[] do
                write(data[i],' ');
end.