关于WQS二分算法以及其一个细节证明

应用分析

　　它的作用就是题目给了一个选物品的限制条件，要求刚好选$m$个，让你最大化（最小化）权值，

　　然后其特点就是当选的物品越多的时候权值越大（越小）。

算法分析

　　我们先不考虑物品限制条件，

　　假定我们要最大化权值。

　　然后其中我们二分一个$C$，表示选一次物品的附加权值，

　　如果我们$C$越大，我们选的物品个数越多，权值越大，

　　于是当选的物品个数大于$m$时，减小$C$，否则增大$C$，

　　最后计算答案的时候去掉$C$值的影响即可。

　　Updata:这回还是讲一讲算法吧-->理论算法分析

　　首先我们拿到一个题，然后发现有一个重要的条件：一共有n个数(下面有时候会称为"点")，要求刚好选$m$个，有某种限制，以某种方式计算和(为了表示方便我暂且称$h(x)$表示选第$x$个点的收益)，选多少个和怎么选都会影响到答案

　　同时我们一般可以得到一个关于n和m的dp方程$dp[i][j] = ......$,其中的复杂度一般都是$O(nm)$及以上的，无法接受，但是经过打表发现：设选$j$的数所的到的dp最大值为$g(j)$，然后发现$g(j)$关于$j$的斜率单调不增，也就是一个上凸包

　　然后如果这题没有刚好选$m$个的限制的时候就可以dp降维的话，那么就可以考虑一下WQS二分

　　首先我们看一下$g$长什么样子(横坐标$x$表示我选多少个数,纵坐标$g(x)$表示我选$x$个数的情况下最大答案)。显然求出$g(m)$就好了。但是问题是你求不出$g(m)$(时间复杂度高)，也就是这个凸包暂时是求不出来的，但是我知道这个形状。

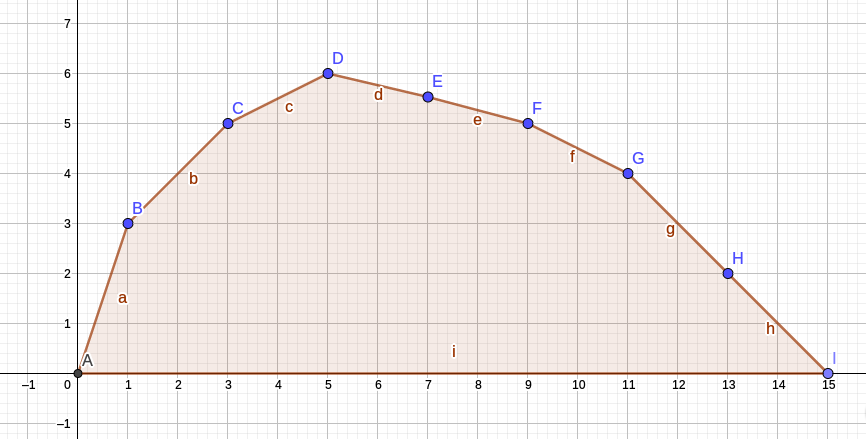
　　于是我们考虑通过用直线切这个凸包去求$g(m)$。然后构造一条直线,去切这个凸包，显然我可以得到一个最大值(切到的那个点就是当前$x$的最大值)，但是这个最大值不一定是取在题目要求的m的，例如我现在令m=7，然后我随便拿一条斜率=$k$的直线去切，但是不是每一条直线都可以使$x=m$：

(为了方便后面我移动了一下$x=7$的点)

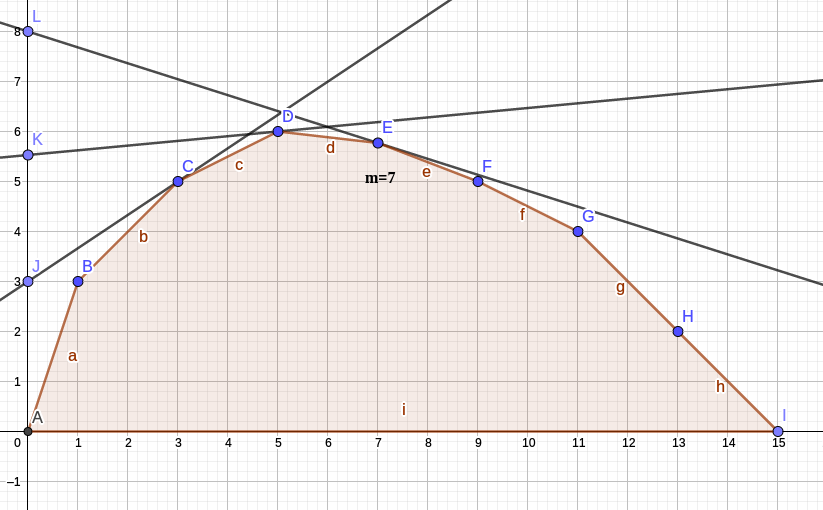
　　我们发现斜率为$k$的直线切这个凸包上的点会切到一些点，每次切到一个点都会切到它的最大值(因为凸包上每一个点都是在固定选多少个数的情况下)

　　然后我们就可以调整直线的斜率，然后直线就可以切到不同的位置，我们发现由于$g(x)$的斜率单调，所以直线斜率$k$切到的点的$x$同样单调，也就是斜率越大$x$越大。

　　我们首先假设去枚举一个斜率为$k$的直线，然后我们要求这个切到了凸包的哪个位置，也就是$x$和$g(x)$，我们如何去求这个东西呢?我们发现斜率为$k$直线切到的点在凸包上可以得到一条完整的直线$y=kx+b$，然后其中切到的点的$b$比其它点的$b$都要大，也就是下图：

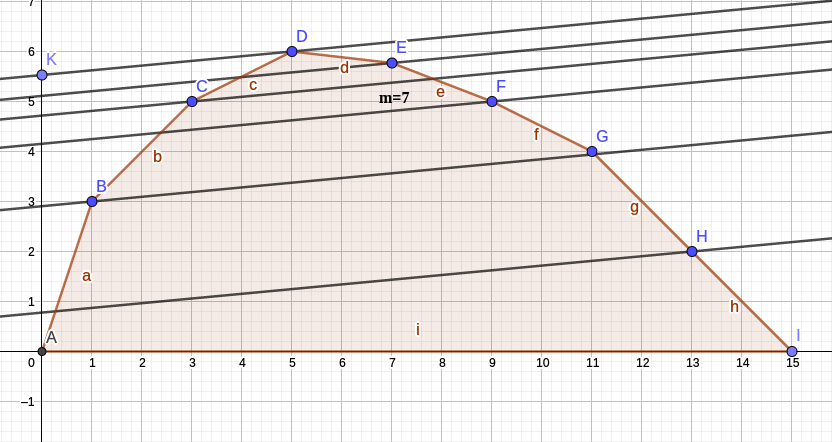
　　然后我们知道$b=y-kx$，换句话说$截距=g(x)-k*x$。怎么求出这个斜率呢？我们观察这个式子，式子等价于：设$f(x)$为我在没有固定选多少个点(但是我已经选了x个点)时的答案(也就是截距)，一开始不求截距的话$f(x)=g(x)$，如果求截距的话我每选一个点那么$f(x)$就$-=k$，最终的答案$f(x)=g(x)-k*x$，也就是我只要把每个数的$h(x)-=k$然后正常求一下在选任意个数的情况下最大$f(x)$是多少。这个东西用dp去做，一般可以做到$O(n)$，而且dp的同时我们还可以知道当$f(x)$最大的时候的$x$是多少。也就意味着我知道了$g(x)$和$x$了！！！

　　然后我现在拿着求出来的$g(x)$和$x$，于是就可以知道我二分大了还是小了，最后直到二分到$m$即可。

　　关于$g(x)$斜率相等，如果不在答案附近那就没有影响，如果在答案附近，那么当我二分出来的$x \geq m$的时候更新答案即可，因为你可以构造出一种合法的方案可以是$x=m$但是答案相等。

问题分析

　　这看起来是没什么问题的，然而我们考虑一件事情，就是如果我们最终要求$C$是个小数才能刚好选出m怎么办？

　　有人说：小数二分啊

　　然而结果是

　　所以小数二分会导致效率不高。

　　我们思考一个问题：我们真的需要得到精确的$C$吗？

　　其实是不需要的，我们只需要在一个那个正确的$C$下的方案即可，因为$C$在最后从答案中减去了。

　　然而可能出现一种情况，我假定二分到了$mid$,$mid$会使选的物品数为$m-1$,$mid+1$会使选的物品数为$m+1$......

　　于是我们思考：能不能不二分到小数？

　　答案是可以的：

　　我们二分，当$选的物品个数 \geq m$时我们更新答案，同时排序上做点手脚。

　　为什么？

　　理论的分析就是上面那张图由于$x$是一个整数，然后你切出来的直线的斜率$k$在一个范围内都是落在同一个$x$点上。

　　接下来可能是一个比较不理论的证明

基于bzoj2654 tree的证明

　　题意大概是：

　　给你一个N个点M条边无向带权连通图，每条边是黑色或白色。让你求一棵最小权的恰好有K条白色边的生成树。

　　解法就是WQS二分+MST

　　然而这题的二分就有上面的问题

　　反证：不存在没有白边黑边相等的情况会出现二分在$mid$和$mid+1$的C不确定

　　首先：如果没有白边黑边相等，我们假定白边权值为$w_1,w_2,w_3..w_x$，黑边$b_1,b_2,b_3...b_y$，两次枚举的C为为$C_1+1=C_2$，$w_1+C_2 \neq b_1 ...$（所以是$white \geq need$） ...

　　那么如果发生二分C值无解的情况，那么两个C1,C2（$C2=C1+1$）导致的至少选出来的白边数量至少差了2（need-1&&need+1），由于差距大于2的和二的情况在下面等价，所以我们先考虑差距为2

　　然后由于如果让两条白边与黑边的权值大小关系改变，那么我们至少需要让2条白边+1后的结果分别大于等于2条黑边

　　所以需要考虑的两种情况就是 有两条白边的权值=两条黑边的权值-1 或 两条白边的权值=两条黑边的权值（基于C1）

　　注意我们还没有考虑连通性，但是这是必要条件

　　由于第一种情况直接不符合题设，我们直接忽略，我们考虑第二种情况，这种情况下C可能在C1、C2中间。由于此时的白边权值在C1下等于黑边权值，那么我们可以发现其实C1状态下选黑边白边边权等价。选择导致的不满足K的答案是合法的，因为我们可能会先统计黑边，使得白边没有被统计然后导致不满足K。然而这个问题我们可以直接通过在排序的时候允许第二关键字（按照颜色（这题白色优先））排序使得这种情况合法化。

　　所以提出的两种无解情况均不存在或者是可以通过算法避免

如果有不严谨出请指正

然而我并没有写证明的经验