dijkstra算法解决单源最短路问题

简介

最近这段时间刚好做了最短路问题的算法报告，因此对dijkstra算法也有了更深的理解，下面和大家分享一下我的学习过程。

前言

呃呃呃，听起来也没那么难，其实，真的没那么难，只要弄清楚思路就很容易了。下面正经的跟大家说下解决问题的过程。

实现过程

我们先用一个d[i]数组表示起点到点i的直接距离，然后从d[i]数组中找最小的值所对应的点，然后看点与点i之间相连的点j,

然后比较d[j]和d[i]+w[i][j]（w[i][j]表示的是点i到点j之间的距离）之间的大小，然后把d[j]和d[i]+w[i][j之间较小的一个赋值给

d[j]，即d[j]=min(d[j],d[i]+w[i][j])。并把点i标记已访问。

然后我们不断的进行上面的操作，直到把所有的点全部访问完毕。

下面是操作过程的流程图

↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓

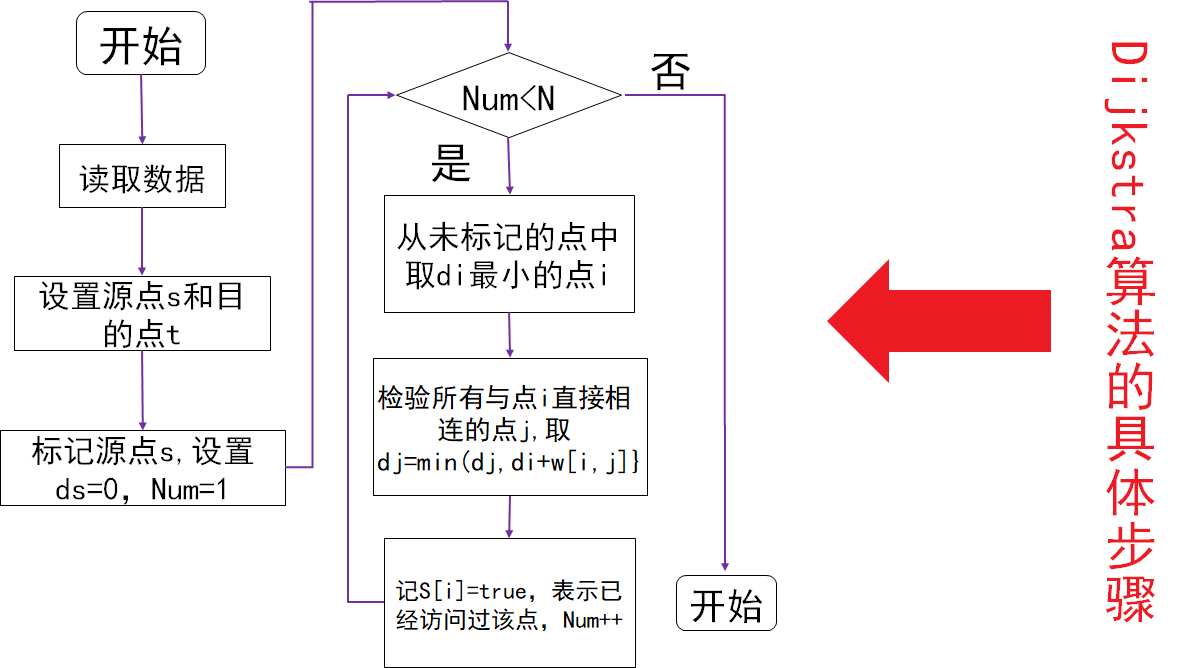
解决问题

题目大概意思：“比如说，在一张无向图中，给了结点数和边的数目让你求出起点到其他各点的最短距离。”

输入数据为：

下面是具体实现的代码：

/*dijkstra算法*/
#include<iostream>
const long long maxint = ;
using namespace std;
const int maxn = ;
int n, m;
int a, b, v, w[maxn][maxn];
int dis[maxn];   //记录起点到别的结点之间的距离
bool s[maxn];    //标记这个点是否在图中
//v0=1;
void dijkstra(int v0) {
    dis[] = ;
    dis[v0] = ;
    s[v0] = true;
    for (int i = ; i <= n; ++i) {    //将每个点到起点的距离更新一下
        dis[i] = w[v0][i];
        s[i] = false;
    }
    while () {
        int min = maxint;
        int u = -;     //标志变量
        for (int j = ; j <= n; ++j) {
            if ((!s[j]) && dis[j] < min) {    //找出不在图里面且权值最小的点
                u = j;                        //将这个点记录下来
                min = dis[j];
            }
        }
        if (u == -) break;
        s[u] = true;   //将这个点放入图中
        for (int j = ; j <= n; ++j) {
            if ((!s[j]) && dis[u] + w[u][j] < dis[j]) {
                dis[j] = dis[u] + w[u][j];   //松弛操作    更新起点到这个点的距离
            }
        }
    }
}
int main() {
    cout << "请输入结点数目和点数: ";
    while (cin >> n >> m && n&&m) {    //输入点的数目和边的数目
        for (int i = ; i <= n; ++i) {
            for (int j = ; j <= n; ++j) {
                w[i][j] = maxint;     //先将每条边的距离弄成很大，后面如果两条边的权值不等于这个很大的数，则说明两个数之间有边
            }
        }
        cout << "请输入两点之间的距离" << endl;
        for (int i = ; i < m; ++i) {
            cin >> a >> b >> v;
            w[a][b] = v;       //因为无向图
            w[b][a] = v;       //所以两个都赋值
        }
        dijkstra();
        for (int i = ; i <= n; ++i) {
            if(w[][i]!=maxint)
            cout << "起点1到点" << i << "的最短距离是" << dis[i] << endl;
            else cout << "起点1到点" << i << "没有路径"<< endl;
        }
    //    cout << dis[n] << endl;
    }
}

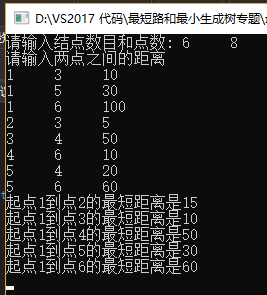
程序运行的结果就是这样的。。。。。。。

好了，到此为止，朴素版本的dijkstra算法就讲完了，感觉好low啊【嘤嘤嘤】

那个那个，估计下一篇博客会把堆优化版本的dijkstra算法更新一下，然后，，，下一次更新不知道是啥时候了，哈哈！