【HDU5306】【DTOJ2481】Gorgeous Sequence【线段树】

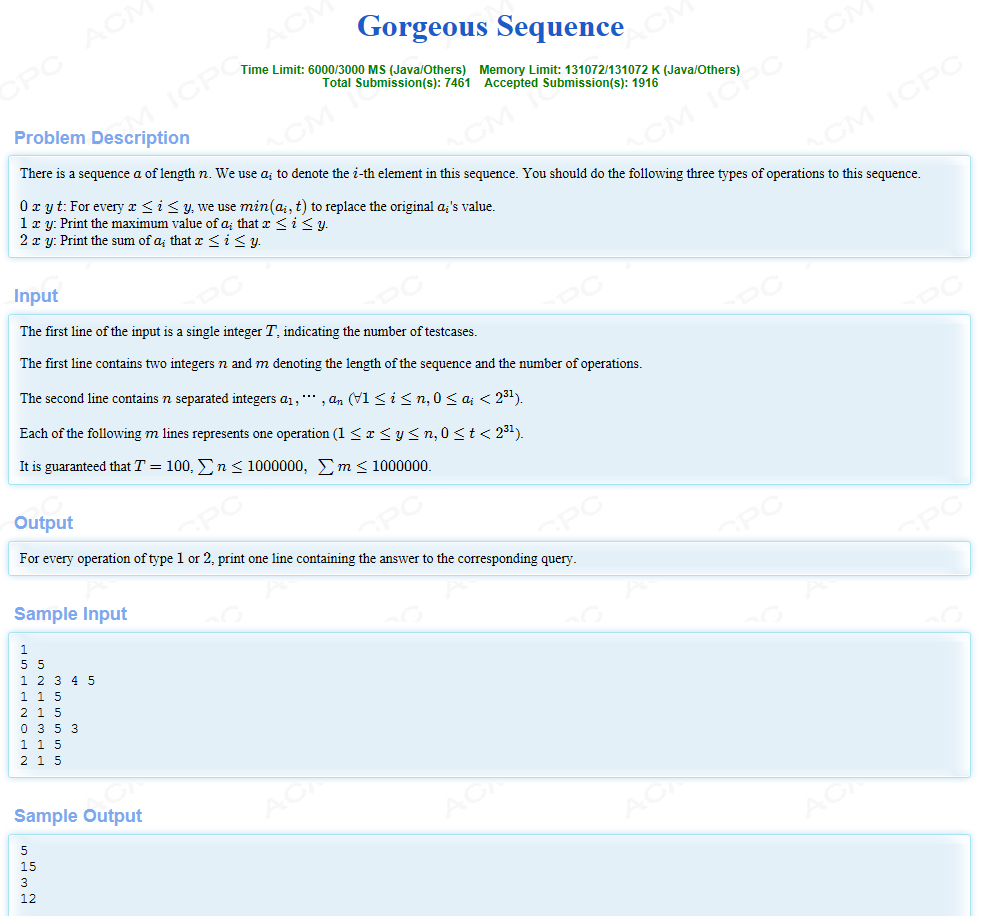
题目大意：给你一个序列a，你有三个操作，0: x y t将a[x,y]和t取min；1：x y求a[x,y]的最大值；2：x y求a[x,y]的sum

题解：首先很明显就是线段树裸题，那么考虑如何维护

区间最大值和区间sum很好维护，0操作不好做，那么考虑怎么快速解决0操作

很容易想到维护区间最大值和区间是否全部相同，这是一个做法，但是时间复杂度上却不正确，但也给了我们一个思路，可以通过维护最大值之类的数来加快操作

一个不行就两个，于是考虑维护次大值，那么每次0操作就有三种情况，一：比区间最大值还大，那么直接返回；二：大于区间次大值小于区间最大值，那么可以直接修改区间；三：小于区间次大值，那么继续递归下去；

这么做是可行的，在更新区间时因为要维护sum值，于是多维护一个区间max有多少个即可

证明略，时间复杂度o(nlog^2n)——来源：吉老师

代码：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<string>
#define ll long long
using namespace std;
int T,n,m;
ll a[];
class Segtree
{
public:
    ll sum[*],mx[*],smx[*],cnt[*],fl[*];

    void pushup(int pos)
    {
        sum[pos]=sum[pos<<]+sum[pos<<|];
        if(mx[pos<<]>mx[pos<<|])
        {
          mx[pos]=mx[pos<<];
          cnt[pos]=cnt[pos<<];
          if(mx[pos<<|]>smx[pos<<])smx[pos]=mx[pos<<|];
          else smx[pos]=smx[pos<<];
        }
        if(mx[pos<<]<mx[pos<<|])
        {
          mx[pos]=mx[pos<<|];
          cnt[pos]=cnt[pos<<|];
          if(mx[pos<<]>smx[pos<<|])smx[pos]=mx[pos<<];
          else smx[pos]=smx[pos<<|];
        }
        if(mx[pos<<]==mx[pos<<|])
        {
          mx[pos]=mx[pos<<];
          cnt[pos]=cnt[pos<<]+cnt[pos<<|];
          if(smx[pos<<]>smx[pos<<|])smx[pos]=smx[pos<<];
          else smx[pos]=smx[pos<<|];
        }
    }
    void pushdown(int pos)
    {
        if(fl[pos]>=)
        {
          if(mx[pos<<]>fl[pos])
          {
            sum[pos<<]-=(mx[pos<<]-fl[pos])*cnt[pos<<];
            fl[pos<<]=mx[pos<<]=fl[pos];
          }
          if(mx[pos<<|]>fl[pos])
          {
            sum[pos<<|]-=(mx[pos<<|]-fl[pos])*cnt[pos<<|];
            fl[pos<<|]=mx[pos<<|]=fl[pos];
          }
          fl[pos]=-;
        }
    }
    void build(int l,int r,int pos)
    {
        if(l==r)
        {
          sum[pos]=mx[pos]=a[l];
          cnt[pos]=;
          fl[pos]=smx[pos]=-;
          return;
        }
        int mid=l+r>>;
        build(l,mid,pos<<);
        build(mid+,r,pos<<|);
        pushup(pos);
        fl[pos]=-;
    }
    void change(int l,int r,int al,int ar,ll v,int pos)
    {
        int mid=l+r>>;
        if(l==al && r==ar)
        {
          if(v>=mx[pos])return;
          if(smx[pos]<v && v<mx[pos])
          {
              sum[pos]-=(mx[pos]-v)*cnt[pos];
              fl[pos]=mx[pos]=v;
              return;
          }
          change(l,mid,al,mid,v,pos<<);
          change(mid+,r,mid+,ar,v,pos<<|);
          pushup(pos);
          return;
        }
        pushdown(pos);
        if(ar<=mid)change(l,mid,al,ar,v,pos<<);
        if(al>mid)change(mid+,r,al,ar,v,pos<<|);
        if(al<=mid && ar>mid){change(l,mid,al,mid,v,pos<<);change(mid+,r,mid+,ar,v,pos<<|);}
        pushup(pos);
    }
    ll askmax(int l,int r,int al,int ar,int pos)
    {
        if(l==al && r==ar)return mx[pos];
        int mid=l+r>>;
        pushdown(pos);
        if(ar<=mid)return askmax(l,mid,al,ar,pos<<);
        if(al>mid)return askmax(mid+,r,al,ar,pos<<|);
        if(al<=mid && ar>mid)
        {
          ll t1=askmax(l,mid,al,mid,pos<<),t2=askmax(mid+,r,mid+,ar,pos<<|);
          return t1>t2?t1:t2;
        }
    }
    ll asksum(int l,int r,int al,int ar,int pos)
    {
        if(l==al && r==ar)return sum[pos];
        int mid=l+r>>;
        pushdown(pos);
        if(ar<=mid)return asksum(l,mid,al,ar,pos<<);
        if(al>mid)return asksum(mid+,r,al,ar,pos<<|);
        if(al<=mid && ar>mid)return asksum(l,mid,al,mid,pos<<)+asksum(mid+,r,mid+,ar,pos<<|);
    }
}segtree;
int main()
{
    scanf("%d",&T);
    while(T--)
    {
      scanf("%d%d",&n,&m);
      for(int i=;i<=n;i++)scanf("%lld",&a[i]);
      segtree.build(,n,);
      int mod,x,y;ll t;
      while(m--)
      {
        scanf("%d",&mod);
        if(mod==)
        {
          scanf("%d%d%lld",&x,&y,&t);
          segtree.change(,n,x,y,t,);
        }
        if(mod==)
        {
          scanf("%d%d",&x,&y);
          printf("%lld\n",segtree.askmax(,n,x,y,));
        }
        if(mod==)
        {
          scanf("%d%d",&x,&y);
          printf("%lld\n",segtree.asksum(,n,x,y,));
        }
      }
    }
    return ;
}

心得：有时候多维护一个次大值能解决很多问题，更多时候在不知道如何证明时间复杂度的情况下往往维护次大值是正确的