洛谷 P4151 BZOJ 2115 [WC2011]最大XOR和路径

//bzoj上的题面太丑了，导致VJ的题面也很丑，于是这题用洛谷的题面

题面描述

XOR（异或）是一种二元逻辑运算，其运算结果当且仅当两个输入的布尔值不相等时才为真，否则为假。 XOR 运算的真值表如下（$1$ 表示真， $0$ 表示假）：

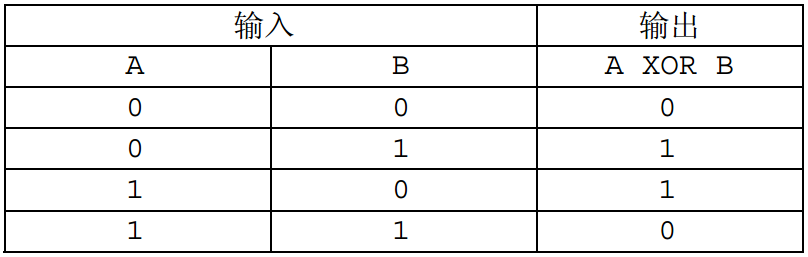
而两个非负整数的 XOR 是指将它们表示成二进制数，再在对应的二进制位进行 XOR 运算。

譬如 $12$ XOR $9$ 的计算过程如下：

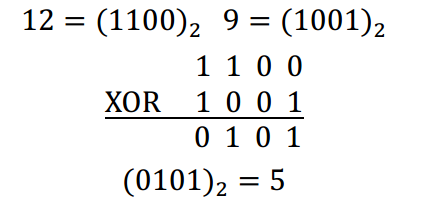
故 $12$ XOR $9$ = 5$。

容易验证， XOR 运算满足交换律与结合律，故计算若干个数的 XOR 时，不同的计算顺序不会对运算结果造成影响。从而，可以定义 $K$ 个非负整数 $A_1，A_2，……，A_{K-1}，A_K$的 XOR 和为

$A_1$ XOR $A_2$ XOR …… XOR $A_{K-1}$ XOR $A_K$

考虑一个边权为非负整数的无向连通图，节点编号为 $1$ 到 $N$，试求出一条从 $1$ 号节点到 $N$ 号节点的路径，使得路径上经过的边的权值的 XOR 和最大。

路径可以重复经过某些点或边，当一条边在路径中出现了多次时，其权值在计算 XOR 和时也要被计算相应多的次数，具体见样例。

输入格式

输入文件 xor.in 的第一行包含两个整数 $N$ 和 $M$，表示该无向图中点的数目与边的数目。

接下来 $M$ 行描述 $M$ 条边，每行三个整数 $S_i$， $T_i$ ， $D_i$，表示 $S_i$ 与 $T_i$ 之间存在一条权值为 $D_i$ 的无向边。

图中可能有重边或自环。

输出格式

输出文件 xor.out 仅包含一个整数，表示最大的 XOR 和（十进制结果）。

输入输出样例

输入 #1

输出 #1

说明/提示

【样例说明】

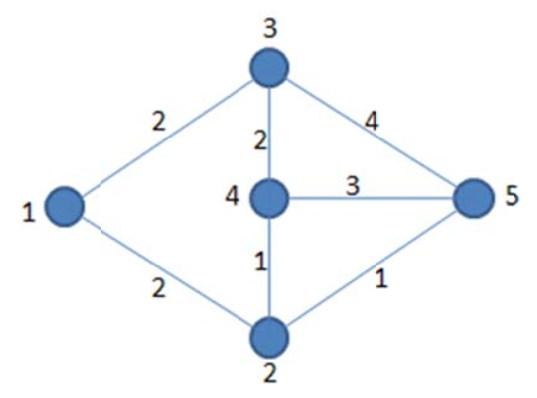
如图，路径$1 \rightarrow 2 \rightarrow 4 \rightarrow 3 \rightarrow 5 \rightarrow 2 \rightarrow 4 \rightarrow 5$对应的XOR和为

$2$ XOR $1$ XOR $2$ XOR $4$ XOR $1$ XOR $1$ XOR $3 = 6$

当然，一条边数更少的路径$1 \rightarrow 3 \rightarrow 5$对应的XOR和也是$2$ XOR $4 = 6$。

【数据规模】

对于 $20 \%$ 的数据，$N \leq 100，M \leq 1000，D_i \leq 10^{4}$；

对于 $50 \%$ 的数据，$N \leq 1000，M \leq 10000，D_i \leq 10^{18}$；

对于 $70 \%$ 的数据，$N \leq 5000，M \leq 50000，D_i \leq 10^{18}$；

对于 $100 \%$ 的数据，$N \leq 50000$， $M \leq 100000$，$D_i \leq 10^{18}$。

解题思路

看了题解可知，这题先dfs一遍图，随便找一条从起点到终点的路，求出路上的异或值，同时把所有搜索到的环的异或值全部加入线性基，然后把那条路上的异或值放到线性基里，找能够异或到的最大值，然后就是答案。敷衍

这题的思想有点像我这学期高数刚学的格林公式，不知道的就别管这个词了。我们从那条路起点$1$出发，到达路中间的一个点$x$，然后离开这条路，通过某一段 $x \rightarrow y$ 走到某个环上的一个点$y$，然后从点$y$开始绕环一周，回到点$y$，再从点$y$通过刚才那段$y \rightarrow x$ 回到点$x$，再接着走完那条路剩下的部分$x\rightarrow n$。由“异或两次同一个数相当于没有异或”的性质可以知道，$x\rightarrow y$和$y\rightarrow x$就互相抵消了，于是答案就是$1\rightarrow n$的异或值再异或上那个环的异或值。再多走几个环，就再多异或几个环就好。

那么为什么最开始随便选一条路就好呢？是这样：假设存在两条路可以从$1$到$n$，那么因为是无向图，这两条路就成了一个环，我们dfs过程中就会把这个环加入线性基。走了其中一条路，再走这个环，就相当于走了另一条路。

源代码

#include<stdio.h>

const int MAXN=5e5+5,MAXM=4e5+5;

typedef long long ull;

int n,m;

struct Edge{

	int nxt,to;

	ull w;

}e[MAXM<<1];

int cnt=1,head[MAXN];

inline void add(int u,int v,ull w)

{

	e[cnt]={head[u],v,w};

	head[u]=cnt++;

	e[cnt]={head[v],u,w};

	head[v]=cnt++;

}

ull b[64]={0};//线性基

inline void addb(ull a)

{

	for(int i=62;~i;i--)

	{

		if(a>>i)

		{

			if(b[i]) a^=b[i];

			else

			{

				b[i]=a;

				return;

			}

		}

	}

}

inline ull mx(ull ans)

{

	for(int i=62;~i;i--)

		if((ans^b[i])>ans) ans^=b[i];

	return ans;

}

bool vis[MAXN];

ull dis[MAXN];//从1搜过来的值

void dfs(int u)

{

	vis[u]=1;

	for(int i=head[u];i;i=e[i].nxt)

	{

		int v=e[i].to;

		if(vis[v])

			addb(dis[v]^dis[u]^e[i].w);

		else

		{

			dis[v]=dis[u]^e[i].w;

			dfs(v);

		}

	}

}

int main()

{

	//freopen("test.in","r",stdin);

	scanf("%d%d",&n,&m);

	while(m--)

	{

		int u,v;

		ull w;

		scanf("%d%d%lld",&u,&v,&w);

		add(u,v,w);

	}

	dfs(1);

	printf("%lld\n",mx(dis[n]));

	return 0;

}