2019 ACM/ICPC 全国邀请赛（西安）J And And And （树DP+贡献计算）

Then n - 1n−1 lines follow. ii-th line contains two integers f_{a_i}(1 \le f_{a_i} < i)fai​​(1≤fai​​<i), w_i(0 \le w_i \le 10^{18})wi​(0≤wi​≤1018) —The parent of the ii-th node and the edge weight between the ii-th node and f_{a_i} (ifai​​(istart from 2)2).

Output

Print a single integer — the answer of this problem, modulo 10000000071000000007.

样例输入1复制

2
12

样例输出1复制

0

样例输入2复制

5
1 0
2 0
3 0
4 0

样例输出2复制

35

题意：
给你一颗n个节点的有根树，让你求那个公式的值。

题解：
首先来看如何判定两个节点的路径权值异或起来为0，
我们借助异或的一个这样的性质 x^x=0
那么我们不妨维护出根节点到所有节点的异或值，
如果两个节点x，y，根节点到x的异或值和根节点到y的异或值相等，那么x异或到y的值就一定为0.

接下来我们考虑一对符合条件的节点x，y对答案的贡献。

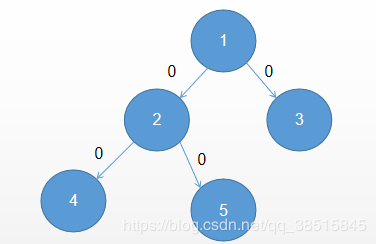
例如这个树中的2和4节点，
我们容易知道，2和4对答案的贡献数量就是4下面那一块（就4这一个节点，）和2右边那一块（2，1，3，5）这四个节点。
那么怎么计算具体的数量呢。

我们把总的贡献数量分为2类来分开求解。
1、计算两个节点在同一条链上。
例如上面说到的2，4就是在同一条链上（这里讲的同一条链上是其中一个节点在和根节点的路径上含有另一个节点。）
那么我们就可以在dfs过程中，在dfs一个节点的子节点之前，把当前节点的贡献加到map里，加的数量用一个变量tmp来维护。
它记录的是该整颗树的节点减去当前节点的子树节点数。那么数量也就是它的子树中的节点如果和它是有效的节点对，
该节点外面可以贡献的节点数量。
当dfs子节点结束后，就返回到之前的数值，对另外一个节点进行dfs，这样可以保证每一次的tmp是针对一个链的。

2、计算不在同一条链上的节点。
同样是dfs，不过这次我们是先dfs，然后更新信息，这样就是一种从下往上更新贡献信息的操作，
因为更新答案是进入dfs就更新的，进入当前节点更新ans的时候，他的子节点还没有加到贡献里，所以就不会重复计算
在同一条立链上的节点，只会计算在不同链上的节点。

本博客参考这个巨巨的博客：https://blog.csdn.net/qq_38515845/article/details/90582561
如果有描述不清楚的地方，可以上这个博客学习。

细节见代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <vector>
#include <iomanip>
#define ALL(x) (x).begin(), (x).end()
#define rt return
#define dll(x) scanf("%I64d",&x)
#define xll(x) printf("%I64d\n",x)
#define sz(a) int(a.size())
#define all(a) a.begin(), a.end()
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
#define pii pair<int,int>
#define pll pair<long long ,long long>
#define gbtb ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define MS0(X) memset((X), 0, sizeof((X)))
#define MSC0(X) memset((X), '\0', sizeof((X)))
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define eps 1e-6
#define gg(x) getInt(&x)
#define db(x) cout<<"== [ "<<x<<" ] =="<<endl;
using namespace std;
typedef long long ll;
ll gcd(ll a, ll b) {return b ? gcd(b, a % b) : a;}
ll lcm(ll a, ll b) {return a / gcd(a, b) * b;}
ll powmod(ll a, ll b, ll MOD) {ll ans = ; while (b) {if (b % )ans = ans * a % MOD; a = a * a % MOD; b /= ;} return ans;}
inline void getInt(int* p);
const int maxn = ;
const int inf = 0x3f3f3f3f;
/*** TEMPLATE CODE * * STARTS HERE ***/
int n;
struct node
{
    int next;
    ll x;
};
ll ans = 0ll;
std::vector<node> son[maxn];
const ll mod = 1e9 + ;
ll num[maxn];
void dfs_num(int x)
{
    // num[x] 代表x的子树的节点个数。
    //
    num[x]++;
    for (auto y : son[x])
    {
        dfs_num(y.next);
        num[x] += num[y.next];
    }
}
map<ll, int> m;
ll tmp = 0ll;
void dfs1(int id, ll s)
{
    // 同一条链
    ans = (ans + 1ll * num[id] * m[s]) % mod;
    for (auto y : son[id])
    {
        tmp = (tmp + 1ll * num[id] - num[y.next]) % mod;
        m[s] = (m[s] + tmp) % mod;
        dfs1(y.next, s ^ y.x);
        m[s] -= tmp;
        m[s] = (m[s] + mod) % mod;
        tmp -= 1ll * num[id] - num[y.next];
        tmp = (tmp + mod) % mod;
    }
}
void dfs2(int id, ll s)
{
    // 不同链
    ans = (ans + 1ll * num[id] * m[s]) % mod;
    for (auto y : son[id])
    {
        dfs2(y.next, s ^ y.x);
    }
    m[s] = (m[s] + num[id]) % mod;
}
int main()
{
    // freopen("D:\\common_text\\code_stream\\in.txt","r",stdin);
    //freopen("D:\\common_text\\code_stream\\out.txt","w",stdout);
    gbtb;
    cin >> n;
    int id; ll x; node temp;
    repd(i, , n)
    {
        cin >> id;
        cin >> x;
        temp.x = x;
        temp.next = i;
        son[id].push_back(temp);
    }
    dfs_num();
    // db(ans);
    dfs1(, 0ll);
    m.clear();
    dfs2(, 0ll);
    cout << (ans + mod) % mod;

    return ;
}

inline void getInt(int* p) {
    char ch;
    do {
        ch = getchar();
    } while (ch == ' ' || ch == '\n');
    if (ch == '-') {
        *p = -(getchar() - '');
        while ((ch = getchar()) >= '' && ch <= '') {
            *p = *p *  - ch + '';
        }
    }
    else {
        *p = ch - '';
        while ((ch = getchar()) >= '' && ch <= '') {
            *p = *p *  + ch - '';
        }
    }
}