平衡查找树之B树

转自：http://www.cnblogs.com/yangecnu/p/Introduce-B-Tree-and-B-Plus-Tree.html

定义

B 树可以看作是对2-3查找树的一种扩展，即他允许每个节点有M-1个子节点。

• 根节点至少有两个子节点
• 每个节点有M-1个key，并且以升序排列
• 位于M-1和M key的子节点的值位于M-1 和M key对应的Value之间
• 其它节点至少有M/2个子节点

下图是一个M=4 阶的B树:

可以看到B树是2-3树的一种扩展，他允许一个节点有多于2个的元素。

B树的插入及平衡化操作和2-3树很相似，这里就不介绍了。下面是往B树中依次插入

6 10 4 14 5 11 15 3 2 12 1 7 8 8 6 3 6 21 5 15 15 6 32 23 45 65 7 8 6 5 4

的演示动画：

B+树是对B树的一种变形树，它与B树的差异在于：

• 有k个子结点的结点必然有k个关键码；
• 非叶结点仅具有索引作用，跟记录有关的信息均存放在叶结点中。
• 树的所有叶结点构成一个有序链表，可以按照关键码排序的次序遍历全部记录。

如下图，是一个B+树:

下图是B+树的插入动画：

B和B+树的区别在于，B+树的非叶子结点只包含导航信息，不包含实际的值，所有的叶子结点和相连的节点使用链表相连，便于区间查找和遍历。

B+ 树的优点在于：

• 由于B+树在内部节点上不好含数据信息，因此在内存页中能够存放更多的key。 数据存放的更加紧密，具有更好的空间局部性。因此访问叶子几点上关联的数据也具有更好的缓存命中率。
• B+树的叶子结点都是相链的，因此对整棵树的便利只需要一次线性遍历叶子结点即可。而且由于数据顺序排列并且相连，所以便于区间查找和搜索。而B树则需要进行每一层的递归遍历。相邻的元素可能在内存中不相邻，所以缓存命中性没有B+树好。

但是B树也有优点，其优点在于，由于B树的每一个节点都包含key和value，因此经常访问的元素可能离根节点更近，因此访问也更迅速。下面是B 树和B+树的区别图：

分析

对于一颗节点为N度为M的子树，查找和插入需要log_M-1N ~ log_M/2N次比较。这个很好证明，对于度为M的B树，每一个节点的子节点个数为M/2 到 M-1之间，所以树的高度在log_M-1N至log_M/2N之间。

这种效率是很高的，对于N=62*1000000000个节点，如果度为1024，则log_M/2N <=4，即在620亿个元素中，如果这棵树的度为1024，则只需要小于4次即可定位到该节点，然后再采用二分查找即可找到要找的值。

应用

B树和B+广泛应用于文件存储系统以及数据库系统中！

如上图，磁盘用读/写头来读写存储在磁性表面的位，而读写头连接到一个传动臂的一端。通过沿着半径轴前后移动传动臂，驱动器可以将读写头定位到任何磁道上，这称之为寻道操作。一旦定位到磁道后，盘片转动，磁道上的每个位经过磁头时，读写磁头就可以感知到位的值，也可以修改值。对磁盘的访问时间分为 寻道时间，旋转时间，以及传送时间。

由于存储介质的特性，磁盘本身存取就比主存慢很多，再加上机械运动耗费，因此为了提高效率，要尽量减少磁盘I/O，减少读写操作。为了达到这个目的，磁盘往往不是严格按需读取，而是每次都会预读，即使只需要一个字节，磁盘也会从这个位置开始，顺序向后读取一定长度的数据放入内存。这样做的理论依据是计算机科学中著名的局部性原理：

当一个数据被用到时，其附近的数据也通常会马上被使用。

程序运行期间所需要的数据通常比较集中。

由于磁盘顺序读取的效率很高（不需要寻道时间，只需很少的旋转时间），因此对于具有局部性的程序来说，预读可以提高I/O效率。

预读的长度一般为页（page）的整倍数。页是计算机管理存储器的逻辑块，硬件及操作系统往往将主存和磁盘存储区分割为连续的大小相等的块，每个存储块称为一页（在许多操作系统中，页得大小通常为4k），主存和磁盘以页为单位交换数据。当程序要读取的数据不在主存中时，会触发一个缺页异常，此时系统会向磁盘发出读盘信号，磁盘会找到数据的起始位置并向后连续读取一页或几页载入内存中，然后异常返回，程序继续运行。

文件系统及数据库系统的设计者利用了磁盘预读原理，将一个节点的大小设为等于一个页，这样每个节点只需要一次I/O就可以完全载入。为了达到这个目的，在实际实现B-Tree还需要使用如下技巧：

每次新建一个节点的同时，直接申请一个页的空间( 512或者1024)，这样就保证一个节点物理上也存储在一个页里，加之计算机存储分配都是按页对齐的，就实现了一个node只需一次I/O。如，将B树的度M设置为1024，这样在前面的例子中，600亿个元素中只需要小于4次查找即可定位到某一存储位置。

同时在B+树中，内节点只存储导航用到的key，并不存储具体值，这样内节点个数较少，能够全部读取到主存中，外接点存储key及值，并且顺序排列，具有良好的空间局部性。所以B及B+树比较适合与文件系统的数据结构。

带有顺序访问指针的B+Tree

一般在数据库系统或文件系统中使用的B+Tree结构都在经典B+Tree的基础上进行了优化，增加了顺序访问指针。

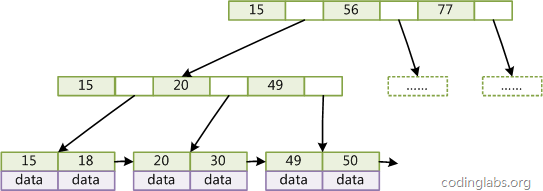
如图4所示，在B+Tree的每个叶子节点增加一个指向相邻叶子节点的指针，就形成了带有顺序访问指针的B+Tree。做这个优化的目的是为了提高区间访问的性能，例如图4中如果要查询key为从18到49的所有数据记录，当找到18后，只需顺着节点和指针顺序遍历就可以一次性访问到所有数据节点，极大提到了区间查询效率。