二叉树之AVL树的平衡实现(递归与非递归)

这篇文章用来复习AVL的平衡操作,分别会介绍其旋转操作的递归与非递归实现,但是最终带有插入示例的版本会以递归呈现.

下面这张图绘制了需要旋转操作的8种情况.(我要给做这张图的兄弟一个赞)后面会给出这八种情况对应平衡实现.

[1]

---

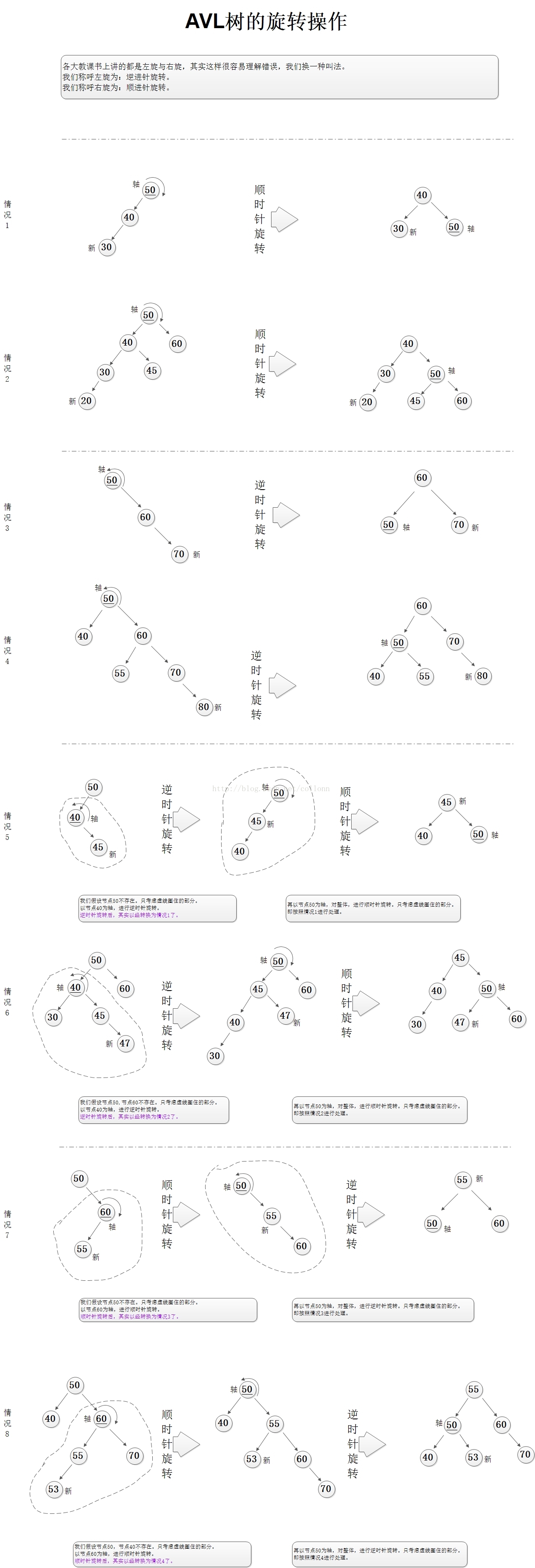
情况1-2:

　　这种需要旋转的结构一般称之为LL型,需要右旋 (顺时针旋转).

　　我用一个图来抽象一下这两个情况,画的不好,我尽量表达吧.

　　

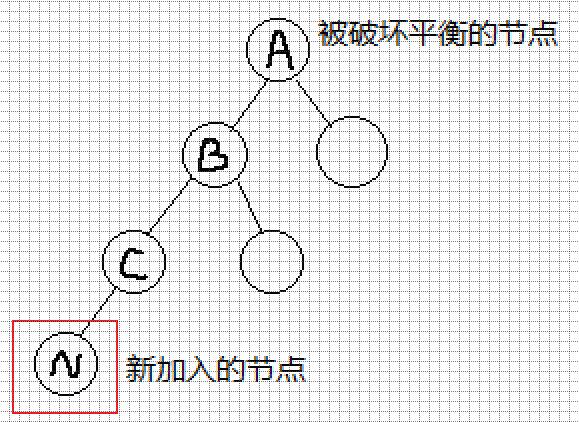
　　此时需要对A进行平衡操作,方法为:

1. 　将A的左子树换为B的右子树.
2. 　　B的右子树换为A.

• 　　非递归实现的代码为:

 void rotate_right(AVLTree &A){

 　　AVLTree leftChild = A->left;

 　　A->left = leftChild->right;

 　　leftChild->right = A;

 　　// 别忘了让父节点建立平衡后的连接

 　　A = leftChild;

 }

　　非递归的操作在旋转前会充分考虑所有的旋转情况,目的是提早调整A下面各节点的高度.

　　之后再进行旋转操作,这一点与递归的不同,可见递归是平衡完后再进行的高度调整.

• 　　递归实现代码为:

 Position CAVLTree::singleRotateWithLeft(Position _K){
     Position K0;
     K0 = _K->left;
     _K->left = K0->right;
     K0->right = _K;

     _K->Height = max(getHeight(_K->left),getHeight(_K->right)) + ;
     K0->Height = max(getHeight(K0->left),getHeight(K0->right)) + ;

     // 返回新的节点以替换
     return K0;
 }

情况3-4:

　　这种需要旋转的结构一般称之为RR型,需要左旋(逆时针旋转).

　　需要对A进行平衡操作,方法为:

1. 　　将A的右子树换为B的左子树;
2. 　　B的左子树换为A

　　

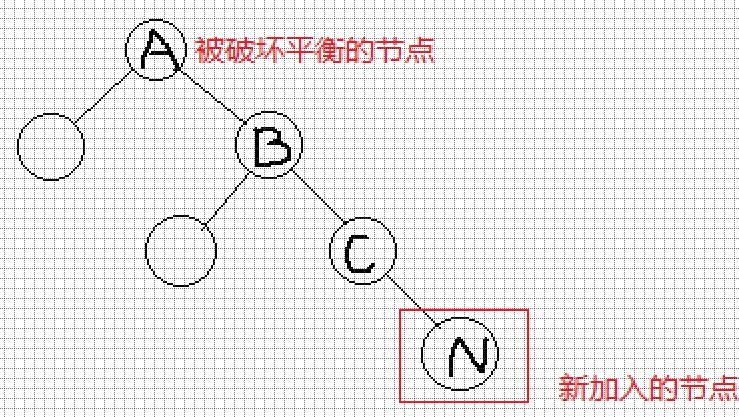
• 　　非递归的实现为:

void rotate_left(AVLTree &A){

    AVLTree rightChild = A->right;

    A->right = rightChild ->left;

    rightChild->left = A;

    A = rightChild;

}

• 　　递归实现为:

Position CAVLTree::singleRotateWithRight(Position _K){
    Position K0;
    K0 = _K->right;
    _K->right = K0->left;
    K0->left = _K;

    _K->Height = max(getHeight(_K->left),getHeight(_K->right)) + ;
    K0->Height = max(getHeight(K0->left),getHeight(K0->right)) + ;
    return K0;
}

情况5-6:　

　　这种需要旋转的结构一般称之为LR型,需要双旋转,即两次单旋.分别为左旋和右旋.

　　需要对A进行平衡操作,方法为:

1. 　　对B(A->left)做左旋
2. 　　对A做右旋

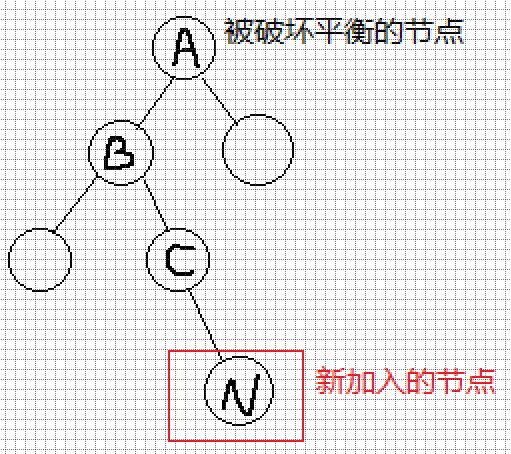
　　这个递归与非递归的方式都是一样的.

• 　　非递归:

rotate_left(A->left);

rotate_right(A);

• 　　递归:

Position CAVLTree::doubleRotateWithLeft(Position _K){
    _K->left = singleRotateWithRight(_K->left);
    return singleRotateWithLeft(_K);
}

　　但是有没有一次性到位的方法呢?有的

　　我把非递归的两个函数展开:

　　发现最后一步都是确定与父节点的关系,并不是旋转中的具体过程,于是可以简化为这样:

AVLTree leftChild = A->left;

AVLTree leftRightChild = leftChild->left;

// 左旋

leftChild->right = leftRightChild->left;

leftRightChild->left = leftChild;

// 右旋

A->left = leftRightChild->right;

leftChild->right = A;

情况7-8:

　　这种需要旋转的结构一般称之为RL型,需要双旋转,即两次单旋.分别为右旋和左旋.

　　需要对A进行平衡操作,方法为:

1. 　　对B进行右旋
2. 　　对A进行左旋

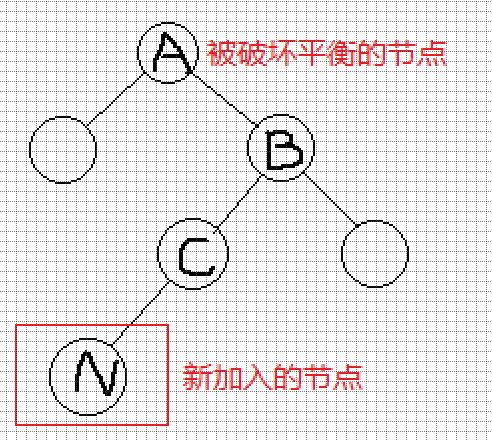
　　同样,递归与非递归版本是一样的.

• 　　非递归:

rotate_right(A->left);

rotate_left(A);

• 　　递归:

Position  CAVLTree::doubleRotateWithRight(Position _K){
    _K->right = singleRotateWithLeft(_K->right);

    return singleRotateWithRight(_K);
}

　　同样,也有一次性到位的方法:

AVLTree rightChild = A->right;

AVLTree rightLeftChild = rightChild->left;

// 右旋

rightChild->left = rightLeftChild->right;

rightLeftChild->right = rightChild;

// 左旋

A->right = rightLeftChild->left;

rightLeftChild->left = A;

---

下面是实现部分:

0.结构声明^[2]:

struct AvlNode;
typedef AvlNode * AvlTree;
typedef AvlNode * Position;

typedef int ELEMENT;

struct AvlNode
{
    AvlNode():data(),left(nullptr),right(nullptr),Height(){}
    ELEMENT data;
    AvlTree left;
    AvlTree right;
    int Height;
};

1.类中提供的API

class CAVLTree
{
public:
    CAVLTree(void);

    ~CAVLTree(void);

    size_t _insert_(ELEMENT &_data);

    int getTreeHeight();

    void showThisTree();

private:

    size_t size;

    AvlTree AvlTreeRoot;
private:

    Position insert_specific(ELEMENT &_data,AvlTree &_T);

    void showThisTree_specific(AvlTree _T);

    int getTreeHeight_specific(AvlTree _T);

    int max(int _a,int _b);

    int getHeight(Position _K);

    // 对于左左的分支,采用右旋
    Position singleRotateWithLeft(Position _K);

    //对于右右的分支,采用左旋
    Position singleRotateWithRight(Position _K);

    // 对于左右的分支,采用先左旋后右旋
    Position doubleRotateWithLeft(Position _K);

    // 对于右左的分支,采用先右旋后左旋
    Position  doubleRotateWithRight(Position _K);
};

2.获取高度:
　　因为在max()函数获取结束后需要+1,所以这里的目的是将叶节点的Height想办法为0.

int CAVLTree::getHeight(Position _K){
    return (_K == nullptr )?-:_K->Height;
}

3.插入操作:

• 　　递归

　　通过回溯的方式找到插入的位置,先平衡后调整高度;

　　哈哈,有一个很有趣的细节为什么同时判断高度差一个是

　　if(getHeight(_T->left) - getHeight(_T->right) == 2)

　　而另一个是

　　if (getHeight(_T->right) - getHeight(_T->left) == 2)

　　因为这里已经知道了插入发生在哪边了,所以肯定是插入的那边会有破坏平衡的可能,不会造成尴尬的(小-大)的局面.

Position CAVLTree::insert_specific(ELEMENT &_data,AvlTree &_T){
    if (!_T)
    {
        _T = new AvlNode;
        _T->data = _data;
        _T->Height = ;
        size++;
    }
    else if(_data < _T->data)
    {
        _T->left = insert_specific(_data,_T->left);
        if(getHeight(_T->left) - getHeight(_T->right) == )
        {
            // 根据新插入的节点所在位置来判断使用什么旋转
            if(_data < _T->left->data)
            {
                // 需要右旋
                _T = singleRotateWithLeft(_T);
            }
            else
            {
                // 需要先左旋后右旋
                _T = doubleRotateWithLeft(_T);
            }
        }
    }
    else if (_data > _T->data)
    {
        _T->right = insert_specific(_data,_T->right);
        if (getHeight(_T->right) - getHeight(_T->left) == )
        {
            if (_data > _T->right->data)
            {
                // 需要左旋
                _T = singleRotateWithRight(_T);
            }
            else
            {
                // 需要先右旋再左旋
                _T = doubleRotateWithRight(_T);
            }
        }
    }

    _T->Height = max(getHeight(_T->left) , getHeight(_T->right)) +  ;

    return _T;
}

　　

• 　　非递归^[3]:

　　可以发现,非递归的实现是先调整高度再平衡,但是要提前考虑所有情况.

　　考虑左子树的情况:

void leftBalance(AVLNode* &t)
{
    AVLNode* lc = NULL;
    AVLNode* rd = NULL;
    lc = t->lchild;
    switch(lc->bf)
    {
        case LH:                    //顺时针旋转(即右旋)
            t->bf = EH;
            lc->bf = EH;
            R_Rotate(t);
            break;

        case EH:                    //删除节点时会发生,插入不会发生
            t->bf = LH;
            lc->bf = RH;
            R_Rotate(t);
            break;

        case RH:                    //先左旋后右旋
            rd = lc->rchild;
            switch(rd->bf)
            {
                case LH:
                    t->bf = RH;
                    lc->bf = EH;
                    break;
                case EH:
                    t->bf = EH;
                    lc->bf = EH;
                    break;
                case RH:
                    t->bf = EH;
                    lc->bf = LH;
                    break;
            }
            rd->bf = EH;
            L_Rotate(t->lchild);//不能写L_Rotate(lc);采用的是引用参数
            R_Rotate(t);
            break;
    }
}

　　考虑右子树的情况:

void rightBalance(AVLNode* &t)
{
    AVLNode* rc = NULL;
    AVLNode *ld = NULL;

    rc = t->rchild;
    switch(rc->bf)
    {
    case RH:                //逆时针旋转(即左旋)
        t->bf = EH;
        rc->bf = EH;
        L_Rotate(t);
        break;
    case EH:                //删除节点时会发生,插入不会发生
        t->bf = RH;
        rc->bf = LH;
        L_Rotate(t);
        break;
    case LH:                //先右旋后左旋
        ld = rc->lchild;
        switch(ld->bf)
        {
        case LH:
            t->bf = EH;
            rc->bf = RH;
            break;
        case EH:
            t->bf = EH;
            rc->bf = EH;
            break;
        case RH:
            t->bf = LH;
            rc->bf = EH;
            break;
        }
        ld->bf = EH;
        R_Rotate(t->rchild);//不能写R_Rotate(rc);采用的是引用参数
        L_Rotate(t);
        break;
    }
}

 总结:

　　递归真是神奇啊,对子树的处理递归的很漂亮,代码量是一方面,代码逻辑的清晰性也是非递归程序鲜有的.

　　用这个来学习递归算法真是好工具,希望对于我后面复习图论有帮助.

　　这篇文章中所述的非递归程序我并没有实现,肯定有疏忽的地方,欢迎大家指正.

完整示例中还有一个showThisTree(),它可以打印出漂亮的平衡二叉树.

相关代码请见我的github

[1]   AVL树的旋转操作 图解 最详细

[2]　left 等价 leftChild,同理,right 也等价 rightChild.

[3]   平衡二叉树(AVL)的插入和删除详解(上)

[4]  参考教材 数据结构与算法分析：C语言描述（原书第2版）[美] MarkAllenWeiss 著