类欧几里德算法（洛谷 P5170

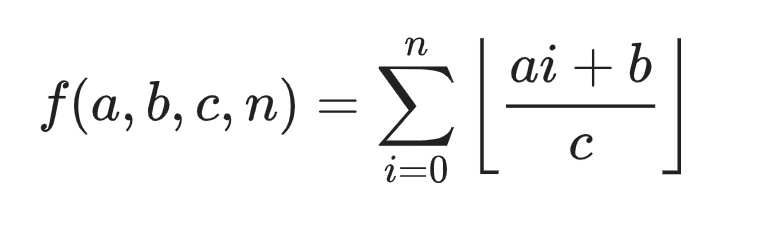
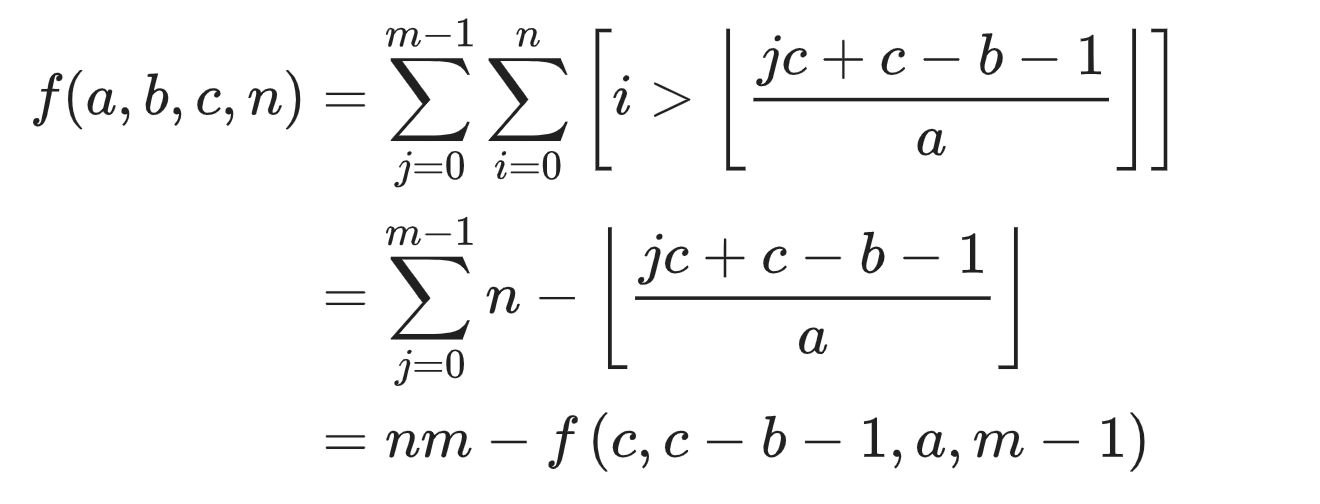
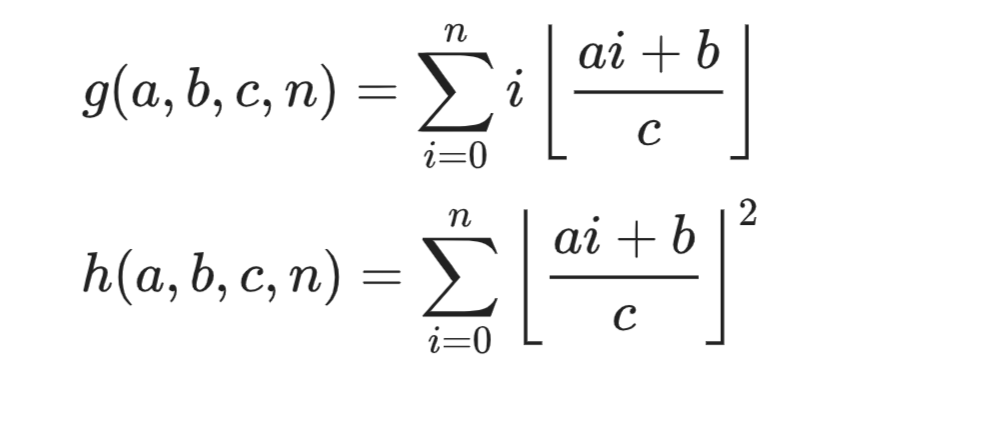
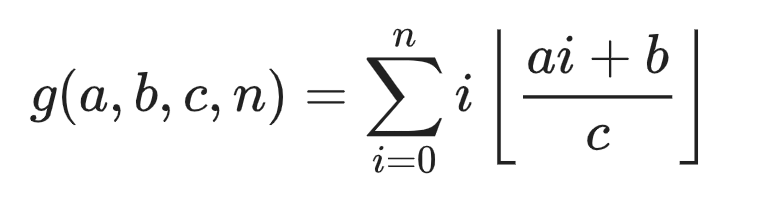
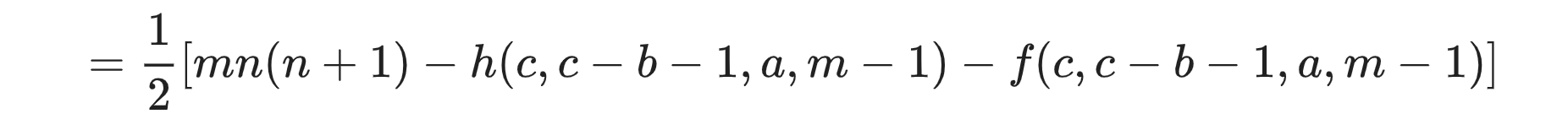
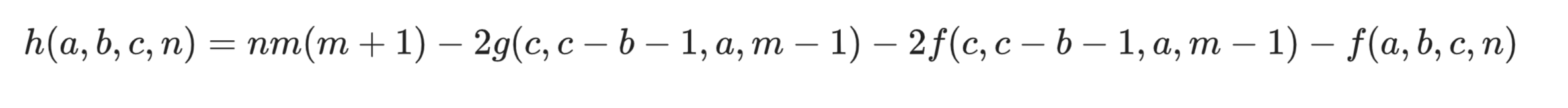
#include <iostream>
#include <cstdio>
#include <queue>
#include <algorithm>
#include <cmath>
#include <cstring>
#define inf 2147483647
#define P 998244353
#define p(a) putchar(a)
#define For(i,a,b) for(long long i=a;i<=b;++i)

using namespace std;
long long T;
long long n,a,b,c;
long long i2 = , i6 = ;//这是2，6在%P意义下的逆元
struct data{
    long long f,g,h;
    data calc(long long n,long long a,long long b,long long c){
         long long ac = a / c, bc = b / c, m = (a * n + b) / c, n1 = n + , n21 = n *  + ;
         data d;
         if (a == ) {
            d.f = bc * n1 % P;
            d.g = bc * n % P * n1 % P * i2 % P;
            d.h = bc * bc % P * n1 % P;
                return d;
        }

        if (a >= c || b >= c){
            d.f = n * n1 % P * i2 % P * ac % P + bc * n1 % P;
            d.g = ac * n % P * n1 % P * n21 % P * i6 % P + bc * n % P * n1 % P * i2 % P;
            d.h = ac * ac % P * n % P * n1 % P * n21 % P * i6 % P +
            bc * bc % P * n1 % P + ac * bc % P * n % P * n1 % P;
            d.f %= P, d.g %= P, d.h %= P;

            data e = calc(n, a % c, b % c, c);

            d.h += e.h +  * bc % P * e.f % P +  * ac % P * e.g % P;
            d.g += e.g, d.f += e.f;
            d.f %= P, d.g %= P, d.h %= P;
                return d;
        }

        data e = calc(m - , c, c - b - , a);
        d.f = n * m % P - e.f, d.f = (d.f % P + P) % P;
        d.g = m * n % P * n1 % P - e.h - e.f, d.g = (d.g * i2 % P + P) % P;
        d.h = n * m % P * (m + ) % P -  * e.g -  * e.f - d.f;
        d.h = (d.h % P + P) % P;
        return d;
    }
}ans;

void in(long long &x){
    long long y=;char c=getchar();x=;
    while(c<''||c>''){if(c=='-')y=-;c=getchar();}
    while(c<=''&&c>=''){ x=(x<<)+(x<<)+c-'';c=getchar();}
    x*=y;
}
void o(long long x){
    if(x<){p('-');x=-x;}
    if(x>)o(x/);
    p(x%+'');
}

signed main(){
    in(T);
    while(T--){
        in(n);in(a);in(b);in(c);
        ans=ans.calc(n,a,b,c);
        o(ans.f);p(' ');o(ans.h);p(' ');o(ans.g);p('\n');
    }
    return ;
}