NOIP模拟测试25「字符串·乌鸦喝水·所陀门王的宝藏（陀螺王）」

字符串

题解

没看出catalan怎么办

dp打表啊!

考虑大力dp拿到30分好成绩!顺便收获一张表

打表发现$C_{n+m}^{m}-C_{n+m}^{m-1}$

仔细观察然后发现其实就是之前的网格那个题

那么我们回顾一下网格那个题

先看最简单的n==m情况

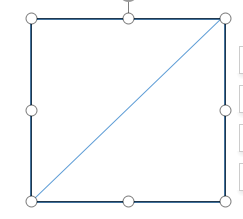
求左下角走到右上角方案数,不能经过中间那条线

考虑大力容斥,首先总方案数$C_{2*n}^{n}$很好求,那么我们现在任务就是求不合法的

我们考虑到如果经过中间那条线我们至少要经过红色那条线,考虑求从左下角超过那条蓝线(不合法)方案数,

如果有红线限制我们好像仍然难以求出,我们怎么消除红线影响

方法非常简单:考虑将正方形翻折,那么我们经过绿线走到右上角就转变为了沿绿线走再沿蓝线走方案,这样我们就摆脱了红线的控制

那么我们就转化为了从左下角走到翻折后多边形所在角在位置

得到$C_{(n+1)+(n-1)}^{n-1}$即$C_{2*n}^{n-1}$

相减即可

那么如果$n!=m$类似$C_{n+m}^{m}-C_{n+m}^{m-1}$,自己画画即可

代码

我不想放了

乌鸦喝水

题解

$55分算法$

先预处理出来能喝多少次

$n*m$ 复杂度,

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define A 1010101
ll cishu,maxn,n,m,all=0;
ll a[A],he[A],xiajiang[A];
int main(){
    scanf("%lld%lld%lld",&n,&m,&maxn);
    for(ll i=1;i<=n;i++){
        scanf("%lld",&a[i]);
    }
    for(ll i=1;i<=n;i++){
        scanf("%lld",&xiajiang[i]);
        he[i]=(maxn-a[i])/xiajiang[i];
    }
    for(ll i=1;i<=m;i++){
        all=1;
        for(ll j=1;j<=n;j++){
            if(he[j]>=cishu){
                cishu++;
                all=0;
            }
        }
        if(all) break;
    }
    printf("%lld\n",cishu);
}

$95分算法$

我们重复枚举了很多无用的状态,当前已经喝不到我们不用再考虑,于是拿链表优化一下

$100分算法$

这种题肯定有性质,这么大的范围一定有性质.

性质: 水少的喝了$k$次那么水多的一定至少也喝了$k$次

我们考虑排序,然而排序后打乱了顺序怎么办,拿一个树状数组维护一下排序前的

我们可以快速算出在当前水壶喝了多少水

思考已知之前喝了$ans$次当前还剩$w$个水壶没喝完,这个水壶能喝$cnt$次

那么它能喝$\frac{cnt-ans}{w}$轮

考虑喝完这么多轮会有剩余,这时用树状数组找sum就完了

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define A 1111111
ll c[A],xiajiang[A],he[A],a[A];
ll n,m,maxn,ans=0;
struct toot{
    ll pos,cnt;
    friend bool operator < (const toot &a,const toot &b){
        return ((a.cnt==b.cnt)?(a.pos<b.pos):(a.cnt<b.cnt));
    }
}que[A];
void add(ll l,ll a){
    for(ll i=l;i<=n;i+=(i&-i))
        c[i]+=a;
}
ll sum(ll l){
    ll sum=0;
    for(ll i=l;i>=1;i-=(i&-i))
        sum+=c[i];
    return sum;
}
int main(){
    scanf("%lld%lld%lld",&n,&m,&maxn);
    for(ll i=1;i<=n;i++){
        scanf("%lld",&a[i]);
    }
    for(ll i=1;i<=n;i++){
        scanf("%lld",&xiajiang[i]);
        he[i]=(maxn-a[i])/xiajiang[i]+1;
        que[i].cnt=he[i],que[i].pos=i;
        add(i,1);
    }
    sort(que+1,que+n+1);
//    printf("que[1]=%lld\n",que[1].cnt);
    for(ll i=1;i<=n;i++){
        add(que[i].pos,-1);
        if(que[i].cnt<=0) continue;
        if(que[i].cnt-ans<=0) continue;
        ll cnt=(que[i].cnt-ans)/(n-i+1);
        if(cnt>=m){
            ans+=m;
            continue;
        }
        if(sum(que[i].pos)<((que[i].cnt-ans)%(n-i+1)))
            cnt++;
        ans+=cnt;
    }
    printf("%lld\n",ans);
}

所驼门王的宝藏(骆驼王)

题解

缩点跑一个类似最长链的东西

数组大小比较谜

代码

#include<bits/stdc++.h>
using namespace std;
#define ll int
#define A 2000010
ll n,m,k,tot=0,cnt=0;
ll id(ll x,ll y){
    return (x-1)*m+y;
}
inline ll read(){
    ll f=1,x=0;char c=getchar();
    while(!isdigit(c)){
        if(c=='-') f=-1;
        c=getchar();
    }
    while(isdigit(c)){
        x=(x<<1)+(x<<3)+(c-'0');
        c=getchar();
    }
    return f*x;
}
ll head[A],nxt[A<<1],ver[A<<1],a[521000],b[521000],c[521000],sz[A],dfn[A],low[A],sta[A],belong[A],f[A];
ll head_[A],nxt_[A<<1],ver_[A<<1];
map< pair<ll,ll>,ll > mp;
ll top=0,toot=0,scc=0,tot_=0;
bool flag[A],vis[A],ins[A];
vector<ll> hang[A],lie[A];
void add(ll x,ll y){
//    printf("x=%d y=%d\n",x,y);
    ver[++tot]=y,nxt[tot]=head[x],head[x]=tot;
}
void add2(ll x,ll y){
//    printf("x=%d y=%d\n",x,y);
    ver_[++tot_]=y;
    nxt_[tot_]=head_[x];
    head_[x]=tot_;
}
void tarjan(ll x){
    dfn[x]=low[x]=++toot;
    sta[++top]=x;
    ins[x]=1;
    for(ll i=head[x];i;i=nxt[i]){
        ll y=ver[i];
        if(!dfn[y]){
            tarjan(y);
            low[x]=min(low[x],low[y]);
        }
        else if(ins[y])
            low[x]=min(low[x],dfn[y]);
    }
    if(low[x]==dfn[x]){
        ll y=0;
        scc++;
        while(1){
            y=sta[top--];
            belong[y]=scc;
            ins[y]=0;
            sz[scc]++;
            if(y==x) break;
        }
    }
}
ll dp(ll x,ll pre){
    if(f[x]) return f[x];
    f[x]=0;
    for(ll i=head_[x];i;i=nxt_[i]){
        ll y=ver_[i];
        ll nx=dp(y,x);
//        printf("x=%d y=%d nx=%d\n",x,y,nx);
        f[x]=max(f[x],nx);
    }
    f[x]+=sz[x];
    return f[x];
}
void rebuilt(){
    for(ll i=1;i<=k;i++){
        for(ll j=head[i];j;j=nxt[j]){
            ll y=ver[j];
            if(belong[i]!=belong[y]){
                add2(belong[i],belong[y]);
            }
        }
    }
}
int main(){
    k=read(),n=read(),m=read();
    for(ll i=1;i<=k;i++){
        a[i]=read(),b[i]=read(),c[i]=read();
        mp[make_pair(a[i],b[i])]=i;
        hang[a[i]].push_back(i);
        lie[b[i]].push_back(i);
    }
    for(ll i=1;i<=k;i++){
        if(c[i]==1){
            for(ll j=0;j<hang[a[i]].size();j++){
                if(i!=hang[a[i]][j])add(i,hang[a[i]][j]);
            }
        }
        if(c[i]==2){
            for(ll j=0;j<lie[b[i]].size();j++){
                if(i!=lie[b[i]][j])add(i,lie[b[i]][j]);
            }
        }
        if(c[i]==3){
        ll _1_=mp[make_pair(a[i]-1,b[i])],_2_=mp[make_pair(a[i]+1,b[i])],_3_=mp[make_pair(a[i],b[i]+1)],_4_=mp[make_pair(a[i],b[i]-1)]
        ,_5_=mp[make_pair(a[i]+1,b[i]+1)],_6_=mp[make_pair(a[i]+1,b[i]-1)],_7_=mp[make_pair(a[i]-1,b[i]-1)],_8_=mp[make_pair(a[i]-1,b[i]+1)];
        if(_1_)    add(i,_1_);
        if(_2_)    add(i,_2_);
        if(_3_)    add(i,_3_);
        if(_4_)    add(i,_4_);
        if(_5_)    add(i,_5_);
        if(_6_)    add(i,_6_);
        if(_7_)    add(i,_7_);
        if(_8_)    add(i,_8_);
        }
    }
    for(ll i=1;i<=k;i++){
        if(!dfn[i])    tarjan(i);
    }
//    for(ll i=1;i<=k;i++){
//        printf("belong=%d\n",belong[id(a[i],b[i])]);
//    }
    rebuilt();
    for(ll i=1;i<=scc;i++){
        if(!f[i])
        dp(i,0);
    }
    for(ll i=1;i<=scc;i++){
        f[0]=max(f[0],f[i]);
    }
    printf("%d\n",f[0]);
}