距离度量以及python实现(二)

接上一篇：http://www.cnblogs.com/denny402/p/7027954.html

7. 夹角余弦(Cosine)

也可以叫余弦相似度。 几何中夹角余弦可用来衡量两个向量方向的差异，机器学习中借用这一概念来衡量样本向量之间的差异。
(1)在二维空间中向量A(x1,y1)与向量B(x2,y2)的夹角余弦公式：

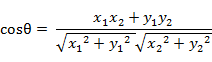
(2) 两个n维样本点a(x11,x12,…,x1n)和b(x21,x22,…,x2n)的夹角余弦
       类似的，对于两个n维样本点a(x11,x12,…,x1n)和b(x21,x22,…,x2n)，可以使用类似于夹角余弦的概念来衡量它们间的相似程度。

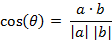
　　即：

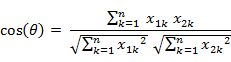
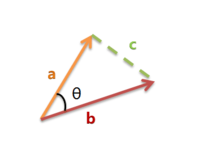
       余弦取值范围为[-1,1]。求得两个向量的夹角，并得出夹角对应的余弦值，此余弦值就可以用来表征这两个向量的相似性。夹角越小，趋近于0度，余弦值越接近于1，它们的方向更加吻合，则越相似。当两个向量的方向完全相反夹角余弦取最小值-1。当余弦值为0时，两向量正交，夹角为90度。因此可以看出，余弦相似度与向量的幅值无关，只与向量的方向相关。

import numpy as np
x=np.random.random(10)
y=np.random.random(10)

#方法一：根据公式求解
d1=np.dot(x,y)/(np.linalg.norm(x)*np.linalg.norm(y))

#方法二：根据scipy库求解
from scipy.spatial.distance import pdist
X=np.vstack([x,y])
d2=1-pdist(X,'cosine')

两个向量完全相等时，余弦值为1，如下的代码计算出来的d=1。

d=1-pdist([x,x],'cosine')

8. 皮尔逊相关系数（Pearson correlation）

(1) 皮尔逊相关系数的定义

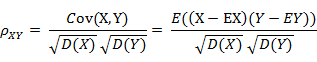
前面提到的余弦相似度只与向量方向有关，但它会受到向量的平移影响，在夹角余弦公式中如果将 x 平移到 x+1, 余弦值就会改变。怎样才能实现平移不变性？这就要用到皮尔逊相关系数（Pearson correlation），有时候也直接叫相关系数。

如果将夹角余弦公式写成：

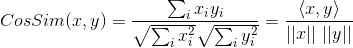
表示向量x和向量y之间的夹角余弦，则皮尔逊相关系数则可表示为：

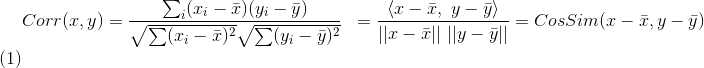
皮尔逊相关系数具有平移不变性和尺度不变性，计算出了两个向量（维度）的相关性。

在python中的实现：

import numpy as np
x=np.random.random(10)
y=np.random.random(10)

#方法一：根据公式求解
x_=x-np.mean(x)
y_=y-np.mean(y)
d1=np.dot(x_,y_)/(np.linalg.norm(x_)*np.linalg.norm(y_))

#方法二：根据numpy库求解
X=np.vstack([x,y])
d2=np.corrcoef(X)[0][1]

相关系数是衡量随机变量X与Y相关程度的一种方法，相关系数的取值范围是[-1,1]。相关系数的绝对值越大，则表明X与Y相关度越高。当X与Y线性相关时，相关系数取值为1（正线性相关）或-1（负线性相关）。

9. 汉明距离(Hamming distance)
(1)汉明距离的定义
       两个等长字符串s1与s2之间的汉明距离定义为将其中一个变为另外一个所需要作的最小替换次数。例如字符串“1111”与“1001”之间的汉明距离为2。
       应用：信息编码（为了增强容错性，应使得编码间的最小汉明距离尽可能大）。

在python中的实现：

import numpy as np
from scipy.spatial.distance import pdist
x=np.random.random(10)>0.5
y=np.random.random(10)>0.5

x=np.asarray(x,np.int32)
y=np.asarray(y,np.int32)

#方法一：根据公式求解
d1=np.mean(x!=y)

#方法二：根据scipy库求解
X=np.vstack([x,y])
d2=pdist(X,'hamming')

10. 杰卡德相似系数(Jaccard similarity coefficient)
(1) 杰卡德相似系数
       两个集合A和B的交集元素在A，B的并集中所占的比例，称为两个集合的杰卡德相似系数，用符号J(A,B)表示。

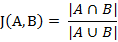
　　杰卡德相似系数是衡量两个集合的相似度一种指标。
(2) 杰卡德距离
       与杰卡德相似系数相反的概念是杰卡德距离(Jaccard distance)。杰卡德距离可用如下公式表示：

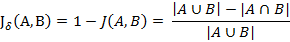
　　杰卡德距离用两个集合中不同元素占所有元素的比例来衡量两个集合的区分度。
(3) 杰卡德相似系数与杰卡德距离的应用
       可将杰卡德相似系数用在衡量样本的相似度上。
　　样本A与样本B是两个n维向量，而且所有维度的取值都是0或1。例如：A(0111)和B(1011)。我们将样本看成是一个集合，1表示集合包含该元素，0表示集合不包含该元素。

在python中的实现：

import numpy as np
from scipy.spatial.distance import pdist
x=np.random.random(10)>0.5
y=np.random.random(10)>0.5

x=np.asarray(x,np.int32)
y=np.asarray(y,np.int32)

#方法一：根据公式求解
up=np.double(np.bitwise_and((x != y),np.bitwise_or(x != 0, y != 0)).sum())
down=np.double(np.bitwise_or(x != 0, y != 0).sum())
d1=(up/down)

#方法二：根据scipy库求解
X=np.vstack([x,y])
d2=pdist(X,'jaccard')

11. 布雷柯蒂斯距离(Bray Curtis Distance)

Bray Curtis距离主要用于生态学和环境科学，计算坐标之间的距离。该距离取值在[0,1]之间。它也可以用来计算样本之间的差异。

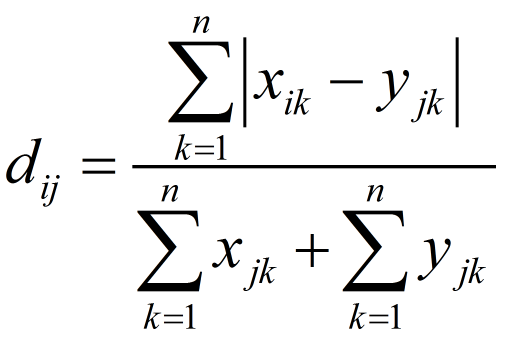
样本数据：

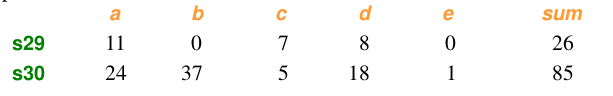
计算：

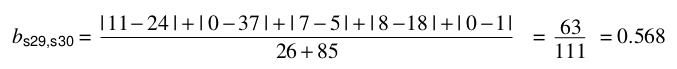
在python中的实现：

import numpy as np
from scipy.spatial.distance import pdist
x=np.array([11,0,7,8,0])
y=np.array([24,37,5,18,1])

#方法一：根据公式求解
up=np.sum(np.abs(y-x))
down=np.sum(x)+np.sum(y)
d1=(up/down)

#方法二：根据scipy库求解
X=np.vstack([x,y])
d2=pdist(X,'braycurtis')