（一） Keras 一元线性回归

视频学习来源

https://www.bilibili.com/video/av40787141?from=search&seid=17003307842787199553

笔记

环境为 anaconda + python3.7

Keras 线性回归

import keras

from keras.layers import Dense

from keras.models import Sequential

import numpy as np

import matplotlib.pyplot as plt

#设置x的数据值

x_data=np.random.rand(100)

np.random.rand(d0,d1,d2……dn)

返回服从“0~1”均匀分布的随机样本值。随机样本取值范围是[0,1)。 

np.random.randn()函数

可以返回服从标准正态分布的随机样本值。

#设置噪声

noise=np.random.normal(0,0.01,x_data.shape)

numpy.random.normal(loc=0.0, scale=1.0, size=None)

loc：均值

scale：float  标准差

size：长度。

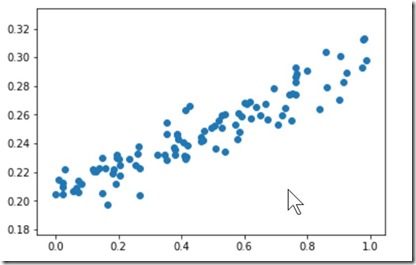
#构造函数

y_data=x_data*0.1+0.2+noise

#画出函数

plt.scatter(x_data,y_data) #scatter散点图

plt.show()

model=Sequential() #建立顺序模型序列

model.add(Dense(units=1,input_dim=1))#输入维度为1，输出维度为1 

添加一个网络层 输入维度为1，输出维度为1 

model.compile(optimizer='sgd',loss='mse') #设置SGD优化模型，

#训练，迭代步为3001次。

for step in range(3001):

    cost=model.train_on_batch(x_data,y_data) #batch 为每次训练的批次

    if step%500 ==0:

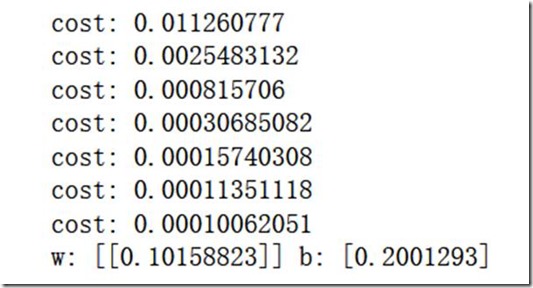
        print('cost:',cost) #每500次输出一次

#打印权值和偏置值

w,b=model.layers[0].get_weights()

print("w:",w,"b:",b)

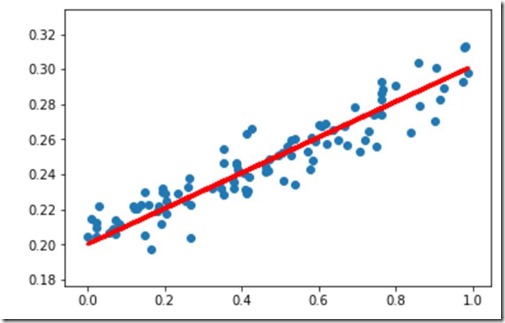
#生成预测值

y_pred=model.predict(x_data)

plt.scatter(x_data,y_data)

plt.plot(x_data,y_pred,'r-',lw=3) #红色，长度为3

plt.show()